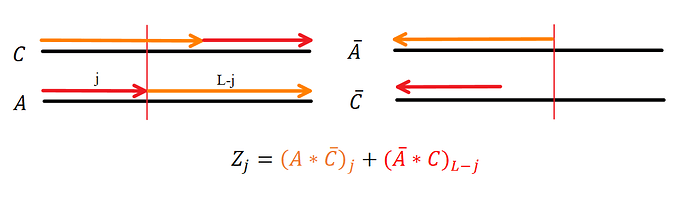ADDBYPERM-Editorial

kugo · June 13, 2022, 7:52am

PROBLEM LINKS:

Setter: Kushagra Goel
Tester: Takuki Kurokawa, Lavish Gupta
Editorialist: Kushagra Goel

DIFFICULTY:

2734

PREREQUISITES:

Basic combinatorics, FFT (NTT)

PROBLEM:

You’re given an array of integers A and a permutation P, each of size N.

The following operation is performed on the array K times:

For each index i (1 \le i \le N), add A_{P_i} to A_i simultaneously.

Find the values of A modulo 998244353, after performing the above operation K times.

QUICK EXPLANATION:

Cycles of the permutation are independent.
For each cycle, observe that the sequence of elements transform to their respective cyclically-shifted dot products with the sequence of binomial coefficients of order K. When the length of this sequence exceeds the size of the cycle, it wraps around and adds. Let’s call this wrapped sequence a pattern.
For a cycle of size m, we evaluate its pattern by iterating over the elements of the binomial sequence in O(K) time. We precompute pattern for all relevant sizes.
For a cycle of size m, the dot products of all its cyclic shifts with its pattern can be computed modulo 998244353 using FFT (number theoretic transform) in O(m \log{m}) time.

EXPLANATION:

Since each cycle of the permutation is independent, WLOG, let’s solve for P_i =(i\%N)+1.

It’s easier to note the pattern from an example:

let A = \{a, b, c, d\}.

iteration 0: A = \{a, b, c, d\}
iteration 1: A = \{a+b, b+c, c+d, d+a\}
iteration 2: A = \{a+2b+c, b+2c+d, c+2d+a...\}
iteration 3: A = \{a+3b+3c+d, b+3c+3d+a...\}
iteration 4: A = \{2a+4b+6c+4d, ...\}

(Note that binomial coefficients of order K are appearing and they start to wrap around the sequence. (a+4b+6c+4d+a))

The above pattern can be proven using induction and the following identity of binomial coefficients: {n \choose k} + {n \choose k-1} = {n+1 \choose k}

Formal Proof

We prove it inductively.

Let V(i, j) be the value of A_i after j applications of the operation by the permutation P given as P_i = (i\%N) + 1. N is the size of A and P.
Proposition: V(i, j) = \sum_{k = 0}^{j} {j \choose k} A_{i+k} \forall i \in [1\dots N] for all non-negative integers j.

Let F(j) be the statement V(i, j) = \sum_{k = 0}^{j} {j \choose k} A_{i+k} \forall i \in [1\dots N]

Assume that for a particular j, F(j) is true.
\implies V(i, j) = \sum_{k = 0}^{j} {j \choose k} A_{i+k} \forall i \in [1\dots N]

By definition, V(i, j+1) = V(i, j) + V(i+1, j).
\implies V(i, j+1) = \sum_{k = 0}^{j} {j \choose k} A_{i+k} + \sum_{k = 0}^{j} {j \choose k} A_{i+1+k}
define {j \choose -1} = {j \choose j+1} = 0,
\implies V(i, j+1) = \sum_{k = 0}^{j+1} {j \choose k} A_{i+k} + \sum_{k = 0}^{j+1} {j \choose k-1} A_{i+k}
\implies V(i, j+1) = \sum_{k = 0}^{j+1} ({j \choose k} + {j \choose k-1}) \cdot A_{i+k}
\implies V(i, j+1) = \sum_{k = 0}^{j+1} {j+1 \choose k} A_{i+k}

Thus, F(j) \implies F(j+1). Since F(0) is trivially true, (V(i, 0) = A_i), F(j) is true for all non-negative j.

So for given K and size of the sequence L, we generate the pattern C as

for i in 0..K:
        C[i % L] += ncr(K, i)

Since the size of the permutation is N, there are O(\sqrt{N}) different cycle sizes and this step takes O(K \sqrt{N} + N) time.

Now we need to find the dot product of C and A over each cyclic shift.

Z_j = \sum_{i=0}^{L-1}A_{(i+j)\%L} \cdot C_{i}

which can be computed in O(L \log{L}) time using FFT as Z = (A * \bar{C}) \% x^L + \overline{(\bar{A}*C)\%x^L}, where \bar{P} is the reversed polynomial of P and * denotes convolution.

TIME COMPLEXITY:

O(K\sqrt{N} + N\log{N})

SOLUTION:

Setter and editorialist's solution

#include "bits/stdc++.h"
using namespace std;

#define all(x)              x.begin(), x.end()

template<int MOD = 998'244'353>
struct Mint {
    int val;
    Mint(long long v = 0) { if (v < 0) v = v % MOD + MOD; if (v >= MOD) v %= MOD; val = v; }
    static int mod_inv(int a, int m = MOD) {
        int g = m, r = a, x = 0, y = 1, q;
        while (r != 0) q = g / r, g %= r, swap(g, r), x -= q * y, swap(x, y);
        return x < 0 ? x + m : x;
    } 
    explicit operator int() const { return val; }
    explicit operator bool()const { return val; }
    Mint& operator+=(const Mint &o) { val += o.val; if (val >= MOD) val -= MOD; return *this; }
    Mint& operator-=(const Mint &o) { val -= o.val; if (val < 0) val += MOD; return *this; }
    static unsigned fast_mod(uint64_t x, unsigned m = MOD) {
           #if !defined(_WIN32) || defined(_WIN64)
                return x % m;
           #endif
           unsigned x_high = x >> 32, x_low = (unsigned) x; unsigned quot, rem;
           asm("divl %4\n": "=a" (quot), "=d" (rem): "d" (x_high), "a" (x_low), "r" (m));
           return rem;
    }
    Mint& operator*=(const Mint &other) { val = fast_mod((uint64_t) val * other.val); return *this; }
    Mint& operator/=(const Mint &other) { return *this *= other.inv(); }
    friend Mint operator+(const Mint &a, const Mint &b) { return Mint(a) += b; }
    friend Mint operator-(const Mint &a, const Mint &b) { return Mint(a) -= b; }
    friend Mint operator*(const Mint &a, const Mint &b) { return Mint(a) *= b; }
    friend Mint operator/(const Mint &a, const Mint &b) { return Mint(a) /= b; }
    Mint& operator++() { val=val==MOD-1?0:val+1; return *this; }
    Mint& operator--() { val=val==0?MOD-1:val-1; return *this; }
    Mint operator++(int32_t) { Mint before = *this; ++*this; return before; }
    Mint operator--(int32_t) { Mint before = *this; --*this; return before; }
    Mint operator-() const { return val == 0 ? 0 : MOD - val; }
    bool operator==(const Mint &other) const { return val == other.val; }
    bool operator!=(const Mint &other) const { return val != other.val; }
    Mint inv() const { return mod_inv(val); }
    Mint operator[](long long p) {
        assert(p >= 0);
        Mint a = *this, res = 1;
        while (p > 0) { if (p & 1) res *= a; a *= a, p >>= 1; }
        return res;
    }
    friend ostream& operator << (ostream &stream, const Mint &m) { return stream << m.val; }
    friend istream& operator >> (istream &stream, Mint &m) { return stream>>m.val; } 
};
using mint = Mint<>;

// need mint

struct NTT_MODS { int MOD, rt, it, pw; } 
ntt_mods[5] = {
    { 7340033, 5, 4404020, 1 << 20 },
    { 415236097, 73362476, 247718523, 1 << 22 },
    { 463470593, 428228038, 182429, 1 << 21},
    { 998244353, 15311432, 469870224, 1 << 23 },
    { 918552577, 86995699, 324602258, 1 << 22 }
};

template<typename mint, int root = 15311432, int root_depth = 23>
struct NTT {
    static vector<mint> rx, ix;

    static void setup () {
        rx = vector(root_depth + 1, mint(root));
        ix = vector(root_depth + 1, 1/mint(root));
        for(int i = 0; i < root_depth; i++) 
            rx[i+1] = rx[i] * rx[i], ix[i+1] = ix[i] * ix[i];
    }

    static void fft (vector<mint> &a, bool invert = false) {
        const int& N = a.size();
        assert(__builtin_popcount(N) == 1);

        for(int i = 1, j = 0; i < N; i++){
            int b = N >> 1;
            while(b & j)
                j ^= b, b >>= 1;
            j ^= b;
            if(j > i)
                swap(a[i], a[j]);
        }

        mint X = 1, iN = mint(N).inv();
        const auto &x = invert? ix: rx;
 
        for(int l = 1, p = 22; l < N; l<<=1, p--)
            for(int s = 0; s < N; s += l+l, X = 1)
                for(int i = s; i < s+l; i++, X *= x[p])
                    a[i+l] = a[i] - X * a[i+l],
                    a[i] = a[i] * 2 - a[i+l];
 
        if(invert) for(auto &v: a) v *= iN;
    }
    
    static vector<mint> convolute_naive (const vector<mint>& a, const vector<mint>& b, size_t MAX = 0) {
        vector c(max((size_t)0, a.size()+b.size()-1), mint());
        if(MAX == 0) MAX = c.size();
        for(int i = 0; i < min(a.size(), MAX); i++)
            for(int j = 0; j < min(b.size(), MAX); j++)
                c[i+j] += a[i] * b[j];
        return (c.resize(MAX), c);
    }

    // In-place convolution modulo x^(MAX)
    static void convolute (vector<mint>& a, vector<mint> b, const size_t MAX = 0){
        if(min(a.size(), b.size()) < 55)
            return void(a = convolute_naive(a, b, MAX));
        
        if(MAX) a.resize(min(MAX, a.size())), b.resize(min(MAX, b.size()));
 
        const int n = (a.size() + b.size()); 
        int m = 1; while(m < n) m <<= 1;
 
        a.resize(m), fft(a);
        b.resize(m), fft(b);

        for(int i = 0; i < m; i++) a[i] *= b[i];

        fft(a, true), a.resize(n-1);
        if(MAX) a.resize(MAX);
    }
 
    // divide and conquer
    static void convolute (vector<vector<mint>>& a, const size_t MAX = 0){
        auto cmp = [&](int i, int j){
            return a[i].size() > a[j].size();
        };
        priority_queue<int, vector<int>, decltype(cmp)> p(cmp);

        for(int i = 0; i < a.size(); i++)
            p.push(i);
        while(p.size() > 1){
            int x = p.top(); p.pop();
            int y = p.top(); p.pop();
            convolute(a[x], a[y], MAX),
            p.push(x), a[y].clear();
        }
        a = {a[p.top()]};
    }
};
template<typename mint, int root, int root_depth> vector<mint> NTT<mint, root, root_depth>::rx;
template<typename mint, int root, int root_depth> vector<mint> NTT<mint, root, root_depth>::ix;
using ntt = NTT<mint, 15311432, 23>;

void brute (int n, int k, vector<int> a, vector<int> p) {
    vector<mint> z;
    for(int x: a) z.push_back(x);

    while(k--) {
        auto v = z;
        for(int i = 0; i < n; i++)
            v[i] = z[p[i]];
        for(int i = 0; i < n; i++)
            z[i] += v[i];
    }

    for(mint x: z) cout << x << ' ';
}

int main(){
    ios_base::sync_with_stdio(0), cin.tie(0);

    ntt::setup();

    int N, K; cin >> N >> K;
    vector A(N, 0), P(N, 0);
    
    for(auto& x: A) cin >> x;
    for(auto& x: P) cin >> x, x--;

    if(1)
        return brute(N, K, A, P), 0;

    vector visited(N, false);
    vector sizes(0, 0);
    vector z(N, mint());


    vector binom(K+1, mint(1));
    for(int i = 1; i <= K; i++)
        binom[i] = binom[i-1] * (K-i+1) / i;

    map<int, vector<mint>> multiplier;

    for(int i = 0; i < N; i++) {
        if(visited[i]) continue;
        
        int j = i;
        vector c(0, 0);
        do {
            c.push_back(j);
            visited[j] = 1;
            j = P[j];
        } while(j != i);

        const int& L = c.size();
        
        if(multiplier.count(L) == 0) {
            vector mul(L, mint(0));
            for(int i = 0; i <= K; i++)
                mul[i % L] += binom[i];
            multiplier[L] = mul;
        }

        vector base(L, mint(0));
        for(int i = 0; i < L; i++)
            base[i] = A[c[i]];

        auto rA = multiplier[L];
        auto rB = base;

        reverse(all(rA)), reverse(all(rB));
        ntt::convolute(rB, multiplier[L], L),
        ntt::convolute(rA, base, L);

        reverse(all(rB));

        for(int i = 0; i < L; i++)
            z[c[i]] = rB[i] + (i? rA[i-1]: 0);

    }

    for(auto x: z)
        cout << x << ' ' ;
}

Tester's solution 1

#include <bits/stdc++.h>
using namespace std;

template <long long mod>
struct modular {
    long long value;
    modular(long long x = 0) {
        value = x % mod;
        if (value < 0) value += mod;
    }
    modular& operator+=(const modular& other) {
        if ((value += other.value) >= mod) value -= mod;
        return *this;
    }
    modular& operator-=(const modular& other) {
        if ((value -= other.value) < 0) value += mod;
        return *this;
    }
    modular& operator*=(const modular& other) {
        value = value * other.value % mod;
        return *this;
    }
    modular& operator/=(const modular& other) {
        long long a = 0, b = 1, c = other.value, m = mod;
        while (c != 0) {
            long long t = m / c;
            m -= t * c;
            swap(c, m);
            a -= t * b;
            swap(a, b);
        }
        a %= mod;
        if (a < 0) a += mod;
        value = value * a % mod;
        return *this;
    }
    friend modular operator+(const modular& lhs, const modular& rhs) { return modular(lhs) += rhs; }
    friend modular operator-(const modular& lhs, const modular& rhs) { return modular(lhs) -= rhs; }
    friend modular operator*(const modular& lhs, const modular& rhs) { return modular(lhs) *= rhs; }
    friend modular operator/(const modular& lhs, const modular& rhs) { return modular(lhs) /= rhs; }
    modular& operator++() { return *this += 1; }
    modular& operator--() { return *this -= 1; }
    modular operator++(int) {
        modular res(*this);
        *this += 1;
        return res;
    }
    modular operator--(int) {
        modular res(*this);
        *this -= 1;
        return res;
    }
    modular operator-() const { return modular(-value); }
    bool operator==(const modular& rhs) const { return value == rhs.value; }
    bool operator!=(const modular& rhs) const { return value != rhs.value; }
    bool operator<(const modular& rhs) const { return value < rhs.value; }
};
template <long long mod>
string to_string(const modular<mod>& x) {
    return to_string(x.value);
}
template <long long mod>
ostream& operator<<(ostream& stream, const modular<mod>& x) {
    return stream << x.value;
}
template <long long mod>
istream& operator>>(istream& stream, modular<mod>& x) {
    stream >> x.value;
    x.value %= mod;
    if (x.value < 0) x.value += mod;
    return stream;
}

constexpr long long mod = 998244353;
using mint = modular<mod>;

mint power(mint a, long long n) {
    mint res = 1;
    while (n > 0) {
        if (n & 1) {
            res *= a;
        }
        a *= a;
        n >>= 1;
    }
    return res;
}

vector<mint> fact(1, 1);
vector<mint> finv(1, 1);

mint C(int n, int k) {
    if (n < k || k < 0) {
        return mint(0);
    }
    while ((int) fact.size() < n + 1) {
        fact.emplace_back(fact.back() * (int) fact.size());
        finv.emplace_back(mint(1) / fact.back());
    }
    return fact[n] * finv[k] * finv[n - k];
}

namespace NTT {
mint root;
int base;
int max_base;
vector<mint> roots;
vector<int> rev;

void ensure_base(int nbase) {
    if (roots.empty()) {
        auto tmp = mod - 1;
        max_base = 0;
        while (tmp % 2 == 0) {
            tmp /= 2;
            max_base++;
        }
        root = 2;
        while (power(root, (mod - 1) >> 1) == 1) {
            root += 1;
        }
        root = power(root, (mod - 1) >> max_base);
        base = 1;
        rev = {0, 1};
        roots = {0, 1};
    }
    if (nbase <= base) {
        return;
    }
    rev.resize(1 << nbase);
    for (int i = 0; i < (1 << nbase); i++) {
        rev[i] = (rev[i >> 1] >> 1) + ((i & 1) << (nbase - 1));
    }
    roots.resize(1 << nbase);
    while (base < nbase) {
        mint z = power(root, 1 << (max_base - 1 - base));
        for (int i = 1 << (base - 1); i < (1 << base); i++) {
            roots[i << 1] = roots[i];
            roots[(i << 1) + 1] = roots[i] * z;
        }
        base++;
    }
}

void ntt(vector<mint>& a) {
    int n = (int) a.size();
    int zeros = __builtin_ctz(n);
    ensure_base(zeros);
    int shift = base - zeros;
    for (int i = 0; i < n; i++) {
        if (i < (rev[i] >> shift)) {
            swap(a[i], a[rev[i] >> shift]);
        }
    }
    for (int k = 1; k < n; k <<= 1) {
        for (int i = 0; i < n; i += 2 * k) {
            for (int j = 0; j < k; j++) {
                mint x = a[i + j];
                mint y = a[i + j + k] * roots[j + k];
                a[i + j] = x + y;
                a[i + j + k] = x - y;
            }
        }
    }
}

vector<mint> multiply(vector<mint> a, vector<mint> b) {
    int need = (int) a.size() + (int) b.size() - 1;
    int nbase = 0;
    while ((1 << nbase) < need) {
        nbase++;
    }
    ensure_base(nbase);
    int sz = 1 << nbase;
    a.resize(sz);
    b.resize(sz);
    ntt(a);
    ntt(b);
    mint inv = mint(1) / mint(sz);
    for (int i = 0; i < sz; i++) {
        a[i] *= b[i] * inv;
    }
    reverse(a.begin() + 1, a.end());
    ntt(a);
    a.resize(need);
    return a;
}
}  // namespace NTT

vector<mint> operator*(const vector<mint>& a, const vector<mint>& b) {
    if (a.empty() || b.empty()) {
        return {};
    } else if (min(a.size(), b.size()) < 150) {
        vector<mint> c(a.size() + b.size() - 1);
        for (int i = 0; i < (int) a.size(); i++) {
            for (int j = 0; j < (int) b.size(); j++) {
                c[i + j] += a[i] * b[j];
            }
        }
        return c;
    } else {
        return NTT::multiply(a, b);
    }
}

vector<mint>& operator*=(vector<mint>& a, const vector<mint>& b) {
    return a = a * b;
}

int main() {
    int n, k;
    cin >> n >> k;
    vector<mint> a(n);
    for (int i = 0; i < n; i++) {
        int v;
        cin >> v;
        a[i] = v;
    }
    vector<int> p(n);
    for (int i = 0; i < n; i++) {
        cin >> p[i];
        p[i]--;
    }
    C(k, 0);
    vector<mint> ans(n);
    vector<bool> done(n);
    vector<vector<mint>> memo(n + 1);
    for (int i = 0; i < n; i++) {
        if (done[i]) {
            continue;
        }
        vector<int> b;
        vector<mint> c;
        int v = i;
        do {
            b.emplace_back(v);
            c.emplace_back(a[v]);
            done[v] = true;
            v = p[v];
        } while (v != i);
        int sz = (int) b.size();
        if (memo[sz].empty()) {
            memo[sz] = vector<mint>(sz);
            for (int j = 0; j <= k; j++) {
                memo[sz][j % sz] += fact[k] * finv[j] * finv[k - j];
            }
        }
        reverse(c.begin(), c.end());
        c *= memo[sz];
        c.emplace_back(0);
        for (int j = 0; j < sz; j++) {
            ans[b[sz - 1 - j]] = c[j] + c[sz + j];
        }
    }
    for (int i = 0; i < n; i++) {
        if (i > 0) {
            cout << " ";
        }
        cout << ans[i];
    }
    cout << endl;
    return 0;
}

Tester's solution 2

#define ll long long
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define mp make_pair
#define fo(i , n) for(ll i = 0 ; i < n ; i++)
//#include<bits/stdc++.h>
#include<iomanip>
#include<cmath>
#include<cstdio>
#include<utility>
#include<iostream>
#include<vector>
#include<string>
#include<algorithm>
#include<map>
#include<queue>
#include<set>
#include<stack>
ll pi = acos(-1) ;
ll z = 998244353 ;
ll inf = 100000000000000000 ;
ll p1 = 37 ;
ll p2 = 53 ;
ll mod1 =  202976689 ;
ll mod2 =  203034253 ;
const int NN = 3e5 ;
ll fact[NN];
ll kcr[NN] ;
ll gdp(ll a , ll b){return (a - (a%b)) ;}
ll ld(ll a , ll b){if(a < 0) return -1*gdp(abs(a) , b) ; if(a%b == 0) return a ; return (a + (b - a%b)) ;} // least number >=a divisible by b
ll gd(ll a , ll b){if(a < 0) return(-1 * ld(abs(a) , b)) ;    return (a - (a%b)) ;} // greatest number <= a divisible by b
ll gcd(ll a , ll b){ if(b > a) return gcd(b , a) ; if(b == 0) return a ; return gcd(b , a%b) ;}
ll e_gcd(ll a , ll b , ll &x , ll &y){ if(b > a) return e_gcd(b , a , y , x) ; if(b == 0){x = 1 ; y = 0 ; return a ;}
ll x1 , y1 ; e_gcd(b , a%b , x1 , y1) ; x = y1 ; y = (x1 - ((a/b) * y1)) ; return e_gcd(b , a%b , x1 , y1) ;}
ll power(ll a ,ll b , ll p){if(b == 0) return 1 ; ll c = power(a , b/2 , p) ; if(b%2 == 0) return ((c*c)%p) ; else return ((((c*c)%p)*a)%p) ;}
ll inverse(ll a ,ll n){return power(a , n-2 , n) ;}
ll max(ll a , ll b){if(a > b) return a ; return b ;}
ll min(ll a , ll b){if(a < b) return a ; return b ;}
ll left(ll i){return ((2*i)+1) ;}
ll right(ll i){return ((2*i) + 2) ;}
ll ncr(ll n , ll r){if(n < r) return 0 ; return ((((fact[n] * inverse(fact[r] , z)) % z) * inverse(fact[n-r] , z)) % z);}
void swap(ll&a , ll&b){ll c = a ; a = b ; b = c ; return ;}
//ios_base::sync_with_stdio(0);
//cin.tie(0); cout.tie(0);
using namespace std ;
#include <ext/pb_ds/assoc_container.hpp> 
#include <ext/pb_ds/tree_policy.hpp> 
using namespace __gnu_pbds; 
#define ordered_set tree<int, null_type,less<int>, rb_tree_tag,tree_order_statistics_node_update>
// ordered_set s ; s.order_of_key(val)  no. of elements strictly less than val
// s.find_by_order(i)  itertor to ith element (0 indexed)
//__builtin_popcount(n) -> returns number of set bits in n


int mod = 998244353; // take mod here
int root = 5 , root_1 = 4404020, root_pw = 1 << 20 ;
int p_root = 3 ; // update this primitive root by checking on net corresponding to particular z
// call this in main()
void init()
{
    ll k = mod ;
    k-- ;
    ll cnt = 0 ;
    while(k % 2 == 0)
    {
        cnt++ ;
        k /= 2 ;
    }
    //cout << "k = " << k << " cnt = " << cnt << endl ; 
    ll prt = p_root ;
    ll rt = power(prt , k , mod) ;
    //rt *= power(2 , cnt-20 , mod) ;
    rt = power(rt , power(2 , cnt-20 , mod) , mod) ;
    rt %= mod ;
    ll rt_1 = inverse(rt , mod) ;

    root = rt ;
    root_1 = rt_1 ;
    return ;
}

void fft(vector<ll> &a, bool invert) {
    int n = a.size();

    for (int i = 1, j = 0; i < n; i++) {
        int bit = n >> 1;
        for (; j & bit; bit >>= 1)
            j ^= bit;
        j ^= bit;

        if (i < j)
            swap(a[i], a[j]);
    }

    for (int len = 2; len <= n; len <<= 1) {
        int wlen = invert ? root_1 : root;
        for (int i = len; i < root_pw; i <<= 1)
            wlen = (int)(1LL * wlen * wlen % mod);

        for (int i = 0; i < n; i += len) {
            int w = 1;
            for (int j = 0; j < len / 2; j++) {
                int u = a[i+j], v = (int)(1LL * a[i+j+len/2] * w % mod);
                a[i+j] = u + v < mod ? u + v : u + v - mod;
                a[i+j+len/2] = u - v >= 0 ? u - v : u - v + mod;
                w = (int)(1LL * w * wlen % mod);
            }
        }
    }

    if (invert) {
        int n_1 = inverse(n, mod);
        for (ll & x : a)
            x = (int)(1LL * x * n_1 % mod);
    }
}

vector<ll> get_ans(vector<ll> a , vector<ll> b)
{

    int k = a.size() + b.size() - 1 ;
    // final result will be of size k. Final ans will be stored in a only.
    int n = 1 ;
    while(n < k)
    {
        n *= 2 ;
    }

    a.resize(n) ;
    b.resize(n) ;

    fft(a , false) ;
    fft(b , false) ;

    fo(i , n)
    {
        a[i] = (1LL * a[i] * b[i]) % (mod) ; 
    }

    fft(a , true) ;

    //a.clear() ;
    a.resize(k) ;

    ll kd = (k+1)/2 ;
    vector<ll> v(kd) ;

    v[0] = a[kd-1] ;
    for(int i = 1 ; i < kd ; i++)
    {
        v[i] = (a[i-1] + a[kd-1+i])%z ;
    }

    return v;    

}



void initialize(ll k)
{
    fact[0] = 1 ;
    for(ll i = 1 ; i < NN ; i++)
    {
        fact[i] = (fact[i-1]*i)%z ;
    }

    for(int i = 0 ; i <= k ; i++)
    {
        kcr[i] = ncr(k , i) ; 
    }
    return ;
}

void get_cycles(ll n, ll perm[], vector<vector<ll> > &cycles)
{
    vector<ll> vis(n+1) ;

    for(int i = 1 ; i <= n ; i++)
    {
        if(vis[i] == 0)
        {
            vector<ll> v ;
            v.pub(i) ;
            ll curr_val = perm[i] ;
            vis[i] = 1 ;

            while(curr_val != v[0])
            {
                v.pub(curr_val) ;
                vis[curr_val] = 1 ;
                curr_val = perm[curr_val] ;
            }

            cycles.pub(v) ;
        }
    }

    return ;
}

void get_values(ll n, ll arr[],vector<vector<ll> > &cycles, vector<vector<ll> > &values)
{
    for(int i = 0 ; i < cycles.size() ; i++)
    {
        vector<ll> v ;
        for(int j = 0 ; j < cycles[i].size() ; j++)
        {
            v.pub(arr[cycles[i][j]]) ;
        }
        values.pub(v) ;
    }
    return ;
}

vector<ll> get_wrapped_values(ll siz, ll k)
{
    vector<ll> v(siz) ;
    int ind = 0 ;

    for(int i = 0 ; i <= k ; i++)
    {
        v[ind] = (v[ind] + kcr[i])%z ;
        if(v[ind] >= z)
            v[ind] -= z ;
        ind++ ;
        if(ind == siz)
            ind = 0 ;
    }
    return v;
}

void solve()
{
    ll n, k ;
    cin >> n >> k ;

    ll arr[n+1];
    ll perm[n+1] ;

    for(int i = 1 ; i <= n ; i++)
        cin >> arr[i] ;
    for(int i = 1 ; i <= n ; i++)
        cin >> perm[i] ;

    initialize(k) ; // initialize factorials and store kcr

    vector<vector<ll> > cycles ;
    get_cycles(n, perm, cycles) ; // decompose permutation into cycles


    vector<vector<ll> > values ;
    get_values(n , arr , cycles, values) ; // get corresponding values from array for different cycles

    map<ll, vector<ll> > wrapped_values ;

    for(int i = 0 ; i < cycles.size() ; i++)
    {
        ll curr_siz = cycles[i].size() ;
        if(wrapped_values.find(curr_siz) == wrapped_values.end())
        {
            wrapped_values[curr_siz] = get_wrapped_values(curr_siz , k) ;
            reverse(wrapped_values[curr_siz].begin() , wrapped_values[curr_siz].end()) ;
        }
    }

    vector<vector<ll> > ans ;
    vector<ll> fin_ans(n+1) ;
    for(int i = 0 ; i < cycles.size() ; i++)
    {
        ll k = cycles[i].size() ;
        vector<ll> curr_ans = get_ans(values[i], wrapped_values[k]) ;
        for(int j = 0 ; j < k ; j++)
        {
            fin_ans[cycles[i][j]] = curr_ans[j] ;
        }
    }

    for(int i = 1 ; i <= n ; i++)
        cout << fin_ans[i] << ' ';
    cout << endl ;

    return ;
}

int main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    #ifndef ONLINE_JUDGE
    freopen("inputf.txt" , "r" , stdin) ;
    freopen("outputf.txt" , "w" , stdout) ;
    freopen("errorf.txt" , "w" , stderr) ;
    #endif
    init() ;
    ll t ;
    // cin >> t ;
    t = 1 ;
   
    while(t--)
    {
        solve() ;
    }
    // cerr << "Time : " << 1000 * ((double)clock()) / (double)CLOCKS_PER_SEC << "ms\n";
 
    return 0;
}

Thanks for reading, hope you enjoyed the problem.

david_s · June 14, 2022, 12:52am

I spotted the binomial coefficients, but had no idea how to proceed from there. Nor did many others in Division 2. I suggest that for a problem as difficult as this there should be a few points awarded for solutions with smaller constraints. For example there could be 5 points for a brute force solution in O(N^3), 15 points for a solution using the binomial coefficients in O(N^2)

phoenix91 · June 14, 2022, 4:24pm

What is reversed polynomial ?

rhymehatch · June 14, 2022, 4:27pm

Interesting.

The final coefficients (after executing k steps) in the cycle correspond to sums of binomials with a step equal to the size of the cycle c, \sum_{i=0}^{k} \binom{n}{X+c*i}.

I thought there was a way to calculate these sums coefficients in O(c \log k). But after that one has to go through every element and multiply the elements in the cycle with these coefficients. I saw it’s O(c^2) which would make it O(n^2) in the worst case.

But I guess in the end there’s no way to compute these sums in O(c \log k) but instead we’re dealing with a convolution of binomial coefficients and array values.

kugo · June 15, 2022, 6:07am

It is the polynomial obtained by reversing the order of coefficients of P. For example,

Let L = 4 and P(x) = 1+2x+4x^2+0x^3.

I define \bar{P}(x) = 0+4x+2x^2+x^3, because the length is 4.

The orange and red lines in the diagram show how the point wise multiplication is performed for a certain j and how it looks like a convolution if you consider A and C in reversed order.

phoenix91 · June 15, 2022, 4:43pm

You should explain the terms you create.
Can’t even find on google.
Bad editorial.

ersshiva · June 16, 2022, 9:26am

For readers:

Multiply polynomial of size m in mlogm time → FFT
Multiply polynomial of size m having integers coefficients uunder a modulo mod in mlogm time → NTT

Google and you’ll find codes for both:
vt mul(vt &a, vt b){
ll tmp = 1;
while(tmp < (ll)a.size() + (ll)b.size())
{
tmp <<= 1;
}
a.resize(tmp);
b.resize(tmp);
NTT(a, false);
NTT(b, false);

for(ll i = 0; i < tmp; i++)
{
    a[i] = Mul(a[i], b[i]);
}

NTT(a, true);
return a;

}

Checkout NTT code here(pretty standard no need to write from scratch every time, have it handy):
https://www.codechef.com/viewsolution/66627719