PROBLEM LINK:
Author: Arvinth Saravanan
Tester: Sankalp Gupta
DIFFICULTY:
HARD.
PREREQUISITES:
DP, basics of graph
PROBLEM:
Given a graph G and values of each node, val[i], find a path such that it maximizes the product of the number of nodes in the path and the minimum of values of the nodes. You can visit a node only once and the nodes are connected to at max two other nodes.
QUICK EXPLANATION:
The graph can be converted to array of arrays and the problem is equivalent to finding the largest rectangular area in histogram
EXPLANATION:
The problem can be broken down into four parts
-
Interpretation as graphs
-
Conversion to an array of arrays data structure
-
Identification of the problem
-
Solving the dynamic programming problem.
PART 1 - INTERPRETATION (EASY)
-
The interpretation of the problem statement as a graph problem is straightforward.
-
Each island is considered as a node, and each path between the islands is considered as edges.
-
Since it’s a two-way path, the graph is undirected
PART 2 - CONVERSION (MODERATE)
-
The graphs are either linear or circular since an island is connected to at max two other islands.
-
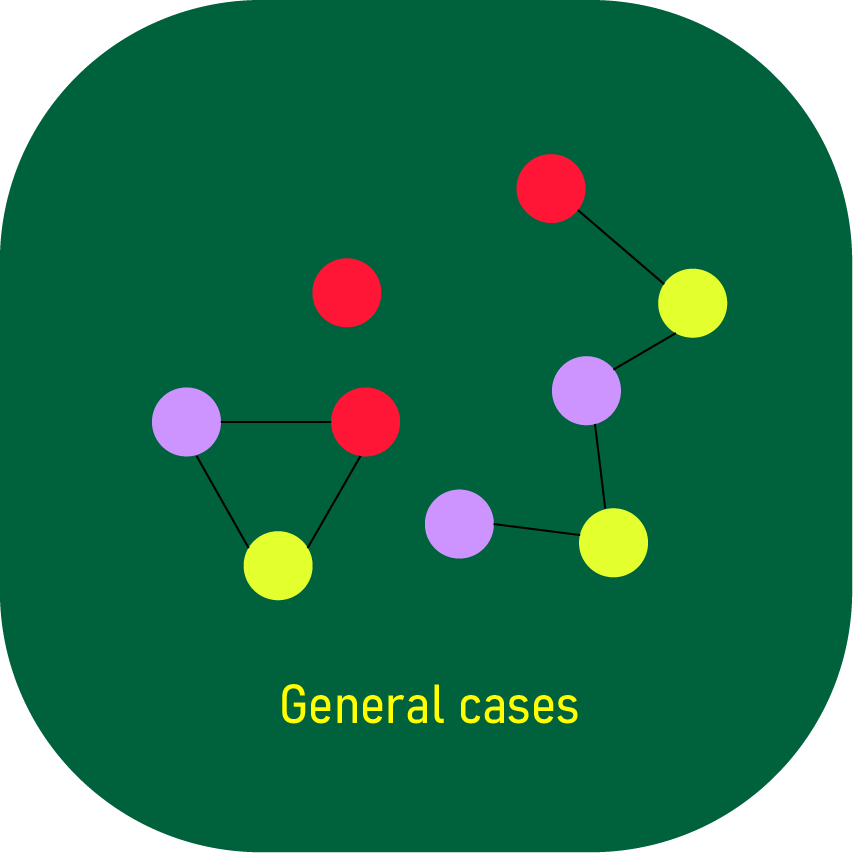
As shown in the illustration a general graph can contain many connected components.
-
A linear graph component can be represented with an array.
-
A node can’t be revisited hence cyclic paths are not allowed. So a cyclic component can also effectively be represented as an array by slicing one of the edges of the node with minimum value. Because, if the node with the minimum value is included then all other nodes in that component can be included without decreasing the virtue level of the group. Thus, each connected components can be represented as an array
-
Hence, the graph can be represented using an array of array say G. Since there’s no path between the connected components traversal is allowed only within an array
PART 3 - IDENTIFICATION (MODERATE)
-
A path can be uniquely identified by the index of the connected component in G, say G[i], and starting and ending nodes in that connected component, G[i][start] and G[i][end].
-
The sum of the virtue level of the group is equal to the product of the number of islands visited and the minimum virtue level of the islands visited
(end - start +1) * min(G[i][start], G[i][start+1], ..., G[i][end])
- The above equation is equivalent to the solution of finding largest rectangular area in a histogram
PART 4 - SOLVING DP (MODERATE)
Largest rectangular area in histogram can be solved in O(n) using stack.
- Create a stack, a running variable j and max\_area
- We consider the rectangle formed from stack.top to current index j
- If j < G[i].size and G[i][j] >= G[i][stack.top] or stack is empty
push j to stack i.e., to consider rectangle starting from index j. Increment j and repeat step 3. - else update max\_area if j < G[i].size and
the area of the rectangle formed between stack.top and j is greater than max\_area and pop stack. Increment j and go to step 3. - if j == G[i].size repeat step 6 until the stack is empty
- update max\_area if the area of the rectangle formed between stack.top and N is greater than max\_area and pop stack. Increment j.
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
void processCycle(vector<pair<long long, long long> > &edges, bool corner[], int m, long long values[]){
int n = edges.size();
bool visited[n];
memset(visited, false, sizeof(visited));
for(int i = 0; i < n; i++){
if(!corner[i])continue;
visited[i] = true;
long long u = edges[i].first;
if(edges[i].first == -1)continue;
long long prev = i;
visited[u] = true;
while(edges[u].second!=-1){
long long v = (edges[u].first==prev)?edges[u].second:edges[u].first;
visited[v] = true;
prev = u;
u = v;
}
}
for(int i = 0; i < n; i++){
if(visited[i])continue;
visited[i] = true;
int min_idx = i;
long long u = edges[i].first;
if(values[u] < values[i]){
min_idx = u;
}
long long prev = i;
visited[u] = true;
while(true){
long long v = (edges[u].first==prev)?edges[u].second:edges[u].first;
if(visited[v]){
int x = edges[min_idx].first;
if(edges[x].first==min_idx){
edges[x].first=-1;
}else{
edges[x].second=-1;
}
corner[x] = true;
corner[min_idx] = true;
break;
}
visited[v] = true;
prev = u;
u = v;
}
}
return;
}
long long getMaxArea(vector<long long> hist)
{
long long n = hist.size();
// Create an empty stack. The stack holds indexes
// of hist[] array. The bars stored in stack are
// always in increasing order of their heights.
stack<long long> s;
long long max_area = 0; // Initialize max area
long long tp; // To store top of stack
long long area_with_top; // To store area with top bar
// as the smallest bar
// Run through all bars of given histogram
long long i = 0;
while (i < n)
{
// If this bar is higher than the bar on top
// stack, push it to stack
if (s.empty() || hist[s.top()] <= hist[i])
s.push(i++);
// If this bar is lower than top of stack,
// then calculate area of rectangle with stack
// top as the smallest (or minimum height) bar.
// 'i' is 'right index' for the top and element
// before top in stack is 'left index'
else
{
tp = s.top(); // store the top index
s.pop(); // pop the top
// Calculate the area with hist[tp] stack
// as smallest bar
area_with_top = hist[tp] * (s.empty() ? i :
i - s.top() - 1);
// update max area, if needed
if (max_area < area_with_top)
max_area = area_with_top;
}
}
// Now pop the remaining bars from stack and calculate
// area with every popped bar as the smallest bar
while (s.empty() == false)
{
tp = s.top();
s.pop();
area_with_top = hist[tp] * (s.empty() ? i :
i - s.top() - 1);
if (max_area < area_with_top)
max_area = area_with_top;
}
return max_area;
}
int main(){
long long n, m;
cin>>n>>m;
vector<pair<long long, long long> > edges(n);
for(long long i = 0; i < n; i++){
edges[i] = pair<long long, long long>(-1, -1);
}
bool corner[n];
memset(corner, true, sizeof(corner));
long long values[n];
for(long long i = 0; i < n; i++)cin>>values[i];
for(long long i = 0; i < m; i++){
long long u, v;
cin>>u>>v;
if(edges[u].first==-1){
edges[u].first = v;
}else{
assert(edges[u].second==-1);
edges[u].second = v;
corner[u] = false;
}
if(edges[v].first==-1){
edges[v].first = u;
}else{
assert(edges[v].second==-1);
edges[v].second = u;
corner[v] = false;
}
}
processCycle(edges, corner, m, values);
long long res=0;
long long answer_length = 2;
for(long long i = 0; i < n; i++){
if(corner[i]){
answer_length = 2;
corner[i] = false;//redundant. Won't be called again
if(edges[i].first==-1){
res=max(res, values[i]);
continue;
}
assert(edges[i].second==-1);
vector<long long> hist;
hist.push_back(values[i]);
long long u = edges[i].first;
corner[u] = false;
hist.push_back(values[u]);
long long prev = i;
while(edges[u].second!=-1){
long long v = (edges[u].first==prev)?edges[u].second:edges[u].first;
hist.push_back(values[v]);
corner[v] = false;
prev = u;
u = v;
answer_length++;
}
int buffer = getMaxArea(hist);
if(buffer > res){
res = buffer;
}
}
}
cout<<res;
}
Tester's Solution
#include<bits/stdc++.h>
#define ll long long int
#define ull unsigned long long int
#define vi vector<int>
#define vll vector<ll>
#define vvi vector<vi>
#define vvl vector<vll>
#define pb push_back
#define mp make_pair
#define all(v) v.begin(), v.end()
#define pii pair<int,int>
#define pll pair<ll,ll>
#define vpii vector<pii >
#define vpll vector<pll >
#define ff first
#define ss second
#define PI 3.14159265358979323846
#define fastio ios_base::sync_with_stdio(false) , cin.tie(NULL) ,cout.tie(NULL)
ll power(ll a,ll b){ ll res=1; while(b>0){ if(b&1) res*=a; a*=a; b>>=1;} return res; }
ll power(ll a,ll b,ll m){ ll res=1; while(b>0){ if(b&1) res=(res*a)%m; a=(a*a)%m; b>>=1;} return res;}
bool pp(int a,int b) {return a>b;}
using namespace std;
vi g[100010];
int a[100010];
vector<bool> vis(100010,false);
queue<int> q;
vi hist;
void bfs(int u){
hist.clear();
hist.pb(a[u]);
q.push(u);
vis[u]=true;
while(!q.empty()){
int v = q.front();
q.pop();
for(int x:g[v]){
if(!vis[x]){
vis[x]=true;
hist.pb(a[x]);
q.push(x);
}
}
}
}
int getMaxArea()
{
stack<int> s;
int n = hist.size();
int max_area = 0;
int tp;
int area_with_top;
int i = 0;
while (i < n)
{
if (s.empty() || hist[s.top()] <= hist[i])
s.push(i++);
else
{
tp = s.top();
s.pop();
area_with_top = hist[tp] * (s.empty() ? i :
i - s.top() - 1);
if (max_area < area_with_top)
max_area = area_with_top;
}
}
while (s.empty() == false)
{
tp = s.top();
s.pop();
area_with_top = hist[tp] * (s.empty() ? i :
i - s.top() - 1);
if (max_area < area_with_top)
max_area = area_with_top;
}
return max_area;
}
void solve(){
int n,m;
cin>>n>>m;
int res=-1;
for(int i=0;i<n;i++) cin>>a[i];
int leaf[n+1]={};
while(m--){
int u,v;
cin>>u>>v;
g[u].pb(v);
g[v].pb(u);
leaf[u]++,leaf[v]++;
}
for(int i=0;i<n;i++){
if(leaf[i]==1&&!vis[i]){
bfs(i);
res=max(res,getMaxArea());
}
}
for(int i=0;i<n;i++){
if(!vis[i]){
bfs(i);
int mn = 1e9,j=0,k;
for(int x:hist){
if(x<mn)
mn=x,k=j;
j++;
}
vi p;
for(j=k;j<hist.size();j++){
p.pb(hist[j]);
}
for(j=0;j<k;j++){
p.pb(hist[j]);
}
hist = p;
res=max(res,getMaxArea());
}
}
cout<<res;
}
int main()
{
fastio;
int t=1;
while(t--){
solve();
}
return 0;
}