Hi,
Here I am going to explain the algorithm for “Strange Number” problem appeared in codechef April 2020 long challenge.
Here is the link to this problem:
Youtube video
C++ Implementation
https://www.codechef.com/viewsolution/31104919
PROBLEM DESCRIPTION
Let A be some positive integer
x = count of all the positive integer divisors of A
k = count of distinct prime factors of A
In the problem, values for x & k are given.
The task is to find out if there exists some integer A with x number of total factors and k number of distinct prime factors.
If some integer A is possible with given x, k values, then, 1 needs to be printed as output otherwise print 0.
Analysis
Any positive integer A can be expressed as follows:
A = (p1 ^ c1) . (p2 ^ c2) .(p3 ^ c3) . . . (pk ^ ck)
where p1, p2, p3 … pk are distinct prime numbers and c1, c2, c3 … ck are their counts respectively.
The total number of factors of A can be determined as follows:
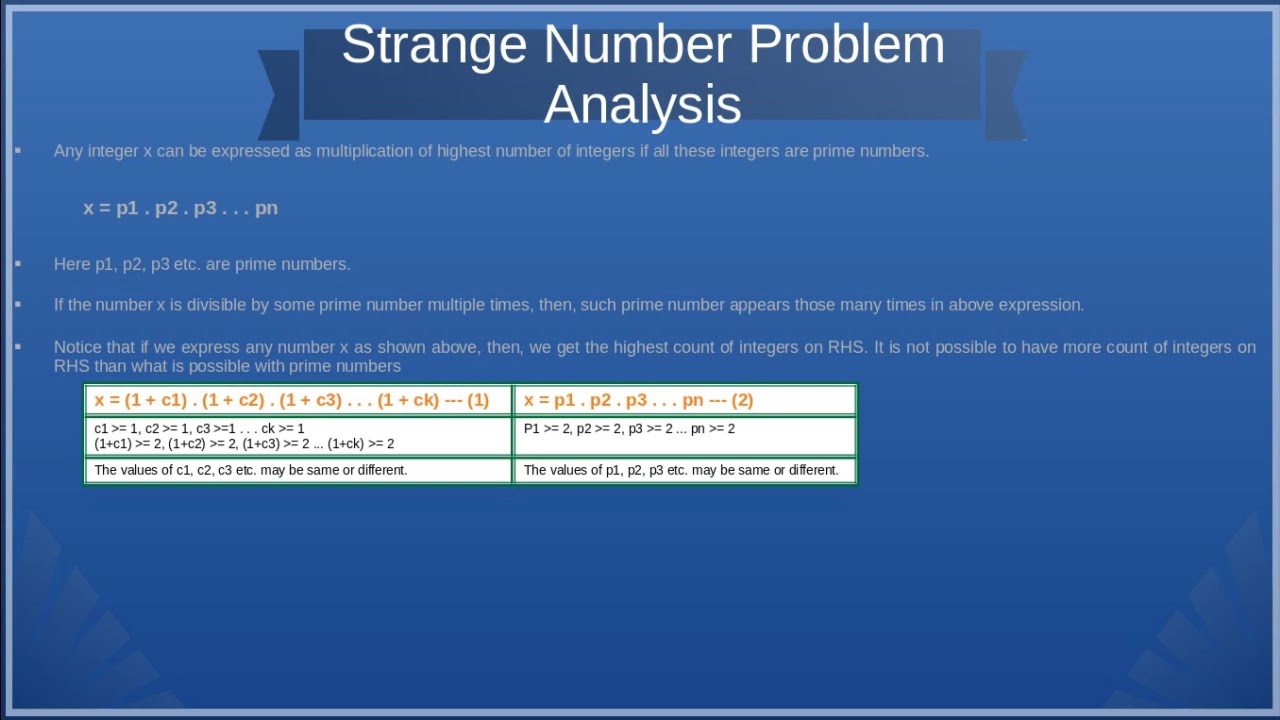
x = (1 + c1) . (1 + c2) . (1 + c3) . . . (1 + ck) — (1)
Note that 1 and that number itself is also included in the count of total number of factors.
c1, c2, c3, …, ck are the counts and all of them needs to be greater than or equal to 1.
The values for c1, c2, c3 etc. need not be distinct. Any positive integer values for these are possible and are valid.
Hence all of these may be distinct; some or all of them may have same values as well.
The only necessary and sufficient condition is all the counts (c1, c2, c3 etc.) needs to be greater than or equal to 1.
The above expression for x suggests that if we can express x as multiplication of k number of integers and if all of these integers are greater than or equal to 2, then, solution is possible.
Hence if x can be expressed as multiplication of k integers, then, number A with x and k is possible.
Now any number x can be expressed as multiplication of highest number of integers if all these integers are prime numbers.
x = p1 * p2 * p3 * p4 * p5 * . . . * pn — (2)
Here p1, p2, p3 etc. are prime numbers.
Some of these primes may have same values.
If the number x is divisible by some prime number multiple times, then, such prime number appears those many times in above expression.
All of the above properties for expression (2) satisfy the requirement to be met in expression (1).
Since the lowest prime number is 2, the expression (2) satisfies the requirement for expression (1).
Since the counts in expression (1) may have same values, it is allowed for expression (2) to contain multiple primes with same values on RHS.
Notice that if we express any number x as above, then, we get the highest count of integers on Right Hand Side(RHS).
It is not possible to have more count of integers on RHS than what is possible with prime numbers.
If the count of prime numbers on RHS in expression (2) is less than k, then solution is not possible.
If it is not possible to express x as multiplication of k integers as mentioned in (1), then, integer A with this x is not possible.
If the count of prime numbers on RHS in expression (2) is equal to k, then, solution is possible.
What if the count of prime numbers on RHS in expression (2) is more than k?
Notice that (1+c1), (1+c2), (1+c3) etc. on RHS of expression (1) need not be primes.
All of these terms are positive integers greater than or equal to 2, because all of the counts (c1, c2, c3 etc.) are positive integers (>=1).
Hence we can multiply multiple prime numbers on RHS of expression (2) to obtain a single integer.
By doing this, we can reduce the count of integers on RHS of expression (2).
So if expression (2) with all prime numbers on RHS contains more count than k terms in it, then, we can make the count on RHS equal to k by multiplying multiple primes.
Suppose k=2 and x is a number with 4 primes on RHS as follows:
x = p1 * p2 * p3 * p4
The count on RHS can be reduced by expressing x as follows:
x = ( p1 * p2 * p3 ) * p4
By considering the value of (p1 * p2 * p3) as a single integer, we have reduced the count on RHS equal to k in this particular case.
No matter how big the count of prime numbers on RHS in expression (2), it is always possible to make the count equal to k by multipying multiple primes in this way.
Algorithm
The algorithm for knowing whether it is possible to have an integer number A for given x and k values is as follows:
-
Obtain the count of prime divisors of x. If x is divisible by some prime number multiple times, then, increment the count those many times.
Notice that this count is as per the count of prime numbers as mentioned in expression (2).
Let us call this count of prime integers as c.
-
If (c >= k) then number A is possible, otherwise not.
Now let us consider some examples:
EXAMPLE 1:
Question: Find out if some integer exists for x = 4 and k = 2
Solution
Express x as multiplication of prime numbers:
x = 4 = 2 * 2
Since the count on RHS is equal to k, some integer A must exist for x=4 and k=2.
Hence it can be concluded that there exists some number A with x = 4 and k = 2
A = 6 is one such example
All the factors of 6 are : [1 2 3 6]
Hence x = 4
And the prime factors are: [2 3]
Hence k = 2
Other examples are: 10, 14, 15, 21 etc.
Let us consider another example.
EXAMPLE 2:
Question: Find out if some integer exists for x = 12 and k = 2
Solution
Express x as multiplication of prime numbers as follows:
x = 12 = 2 * 2 * 3
The count on RHS is 3 which is greater than k = 2.
Hence the solution is possible i.e. some integer A must exist with x = 12 and k = 2.
A = 72 is one such example.
All the facors of 72 are: [1 2 3 4 6 8 9 12 18 24 36 72]
Hence x = 12
And k = 2 because the list of factors has two primes numbers: [2 3] in it.
Other examples are: 675, 6125 etc.