PROBLEM LINK:
DIFFICULTY:
EASY-MEDIUM
PREREQUISITES:
Dijkstra’s algorithm, Prim’s algorithm
PROBLEM:
Given an undirected weighted graph, find whether there exist a shortest path tree(rooted at node 0) which is also the minimum spanning tree.
QUICK EXPLANATION:
If the weight of the Minimum Spanning Tree(MST) is equal to the weight of some Shortest Path Tree then the answer is YES else NO. Now among many shortest path trees, only the one whose weight is minimum can possibly also be the minimum spanning tree. So to find the shortest path tree with minimum weight we have to modify Dijkstra’s algorithm such that if there exist more than one path to a vertex from root which yields the same distance from root then we give preference to that path whose last edge added is minimum.
EXPLANATION:
Weight of any tree is greater of equal to weight of MST,therefore weight of any SPT will also be greater or equal to weight of MST. So if any SPT has weight equal to weight of MST, then that SPT is also a MST since it connects all vertices. Now, the question basically boils down to finding the minimum weight shortest path tree(rooted at vertex 0). Once we find the weight of that tree and if it is equal to weight of the minimum spanning tree(MST) then answer is YES else NO. See the example below where there are 2 shortest path tree(SPT) and one of them is also the MST.
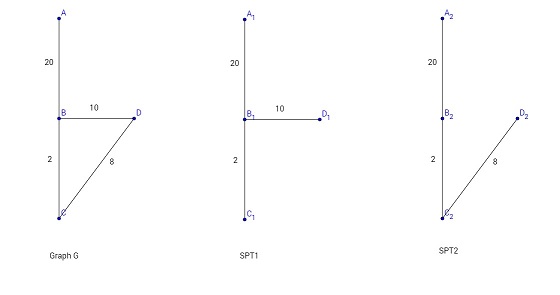
Now to find the minimum weight shortest path tree we will modify the standard Dijkstra. In Dijkstra, we initially assign distance equal to 0 to vertex 0 and insert pair < distance, vertex > = <0,0> into a heap. Then we repeatedly extract min and relax all the neighbours and insert the pairs whose distances are reduced. Now instead of that we will insert a triplet < distance, lastEdge, vertex >. So the heap structure will first follow the distance field and if distances are equal then it will follow lastEdge field. We can note this in the above graph, when vertex B is extracted, the algorithm will insert two triplets <22,2,C> and <30,10,D>. Then vertex C will be extracted and the triplet <30,8,D> will be inserted. Now notice that there are 2 shortest paths from A to D (A-B-D and A-B-C-D) but the path A-B-C-D should be preferred and this is exactly the case here as while inserting <30,8,D> we will update the lastEdge added.
Below is pseudo code of the main loop of the modified Dijkstra.
priority_queue<triplet> Q;
Q.push(0,0,0);
while(Q is not empty)
u = Q.third;
Q.pop();
if(visited[u]) continue;
for all neighbour (w, v) of u where w is the edge weight
if( !visited[v] && (dist[u] + w < dist[v] || (dist[u] + w == dist[v] && w < lastAdded[v])) )
dist[v] = dist[u] + w;
lastAdded[v] = w;
Q.push(dist[v], lastAdded[v], v);
visited[u] = true;
Now we just have to add all the values in lastAdded array and that will be our answer which is compared with weight of the MST. Further we also have to take care of the case when graph is disconnected, which can be easily accomplished by initializing lastAdded to infinity. After running the modified Dijkstra, if any of the vertex has lastAdded[] set to infinity then the answer is NO.
The proof of correctness of this algorithm is same as that of proof of correctness of prim’s algorithm which can be found in Introduction to Algorithms by CLRS.
EDITORIALIST’S SOLUTION:
Editorialist’s solution can be found here.