PROBLEM LINK:
Author: Anudeep Nekkanti
Tester: Gerald Agapov
Editorialist: Praveen Dhinwa
DIFFICULTY:
HARD
PREREQUISITES:
Min Cost Max Flow
PROBLEM:
You are given tree with N nodes each node being numbered between 1 and N, Node 1 is the root node. All the nodes have values given by value array.
You are requested to answer some queries of following kind.
Each query contains m nodes to be inserted in the given particular order. Adding a vertex v to vertex u means adding v as a child of vertex u.
Cost of this operation is value[u] * value[v]. You will need to pay extra cost equal to y if node u contains at least x children.
For each query, you need to answer minimum cost required for adding the given vertices.
QUICK EXPLANATION
We can solve it by application of min cost max flow algorithm. For brief explanation you can see the pictures directly, for detailed explanation you are recommended to read the next section.
EXPLANATION
Let us consider an entirely different problem, we are given two arrays a and b with n and m elements respectively (n > m).
Cost of matching ith element of array a to the jth element of array b is equal to a[i] * b[j]. You have to find minimum cost of
matching all the elements of smaller array (ie. b). to some of the elements of the larger array.
This problem can be solved by greedy algorithm (sort the smallest m element of array a in increasing and sort the elements of b in decreasing order).
Note that this problem can also be solved by min cost max flow algorithm.
In our case, the cost function was a[i] * b[j], We can prove out greedy algorithm for this simple case by exchange argument, but when the cost function starts getting complex, most of time greedy algorithms will fail and your final resort is to apply min cost max flow.
Note that if we make a restriction in the problem that the newly added vertices in the query should only be added to the vertex of the tree with initial n nodes. i.e. we are not allowed to add the vertex given in query to some of the previously added vertices in the query. Let us see how this assumption simplifies things a lot.
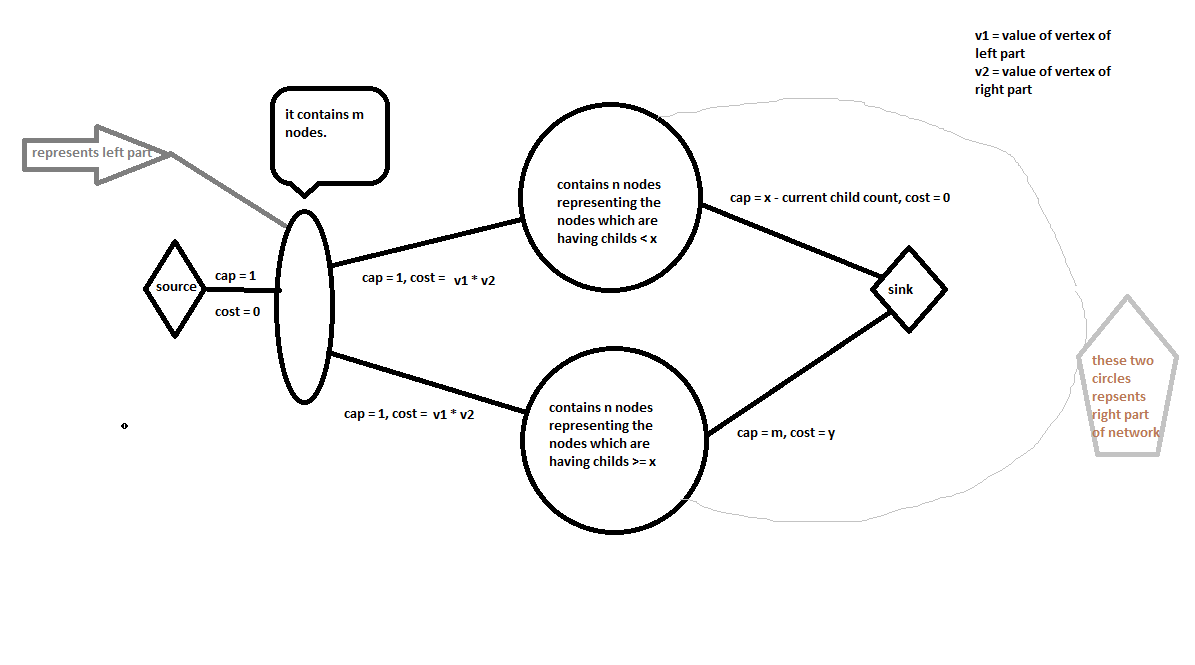
Our network diagram is going to be similar to the previous problem (matching of an array a with b) with small changes. Only problem we have to consider how we are going to handle the nodes which will have >= x child after addition of some vertex. See the following network diagram.
-
In the right part of the network, we have made two copies of n vertices.
Each vertex v in first section of right part (upper circle in right part) is connected with sink having capacity of x - child[v] and cost of 0.
Note that capacity of x - child[i] signifies that we can add at most x - child[i] vertices to node i.
According to problem statement, On all those additions we don’t need to pay any extra cost, hence cost of the edge is equal to 0. -
Each vertex v in second section of right part (lower circle in right part) is connected to sink with capacity
of infinity (in our case as maximum flow can be at most m, hence m) and cost equal to y because we need to pay extra cost of y if we are going to add a vertex to some vertex with >= x children.
Now lets justify why the above network works?
-
If a node v has has < x children, then the flow will go through first section rather than second section in the right part.
Proof:
If we are going to pass flow through second section in the right part rather than the first section, we need to pay cost of y more.
Hence min cost max flow algorithm will pass flow through the edges where the cost is less. -
If a node has >= x children, we need to pay the extra cost. According to our construction, we can not pass flow through some vertex in
first section because its capacity with sink will be utilized (because max flow allowed through edge is m - child[v]) and residual capacity will become zero.
Now the problem turns into a simple min cost max flow application with the above given network.
Now let us come back to our original problem.
OUR ORIGINAL PROBLEM
Now lets take the problem in its original form, From previous section we have get an idea of handling number of children being less than x condition.
Let us have a look at the structure of the network.
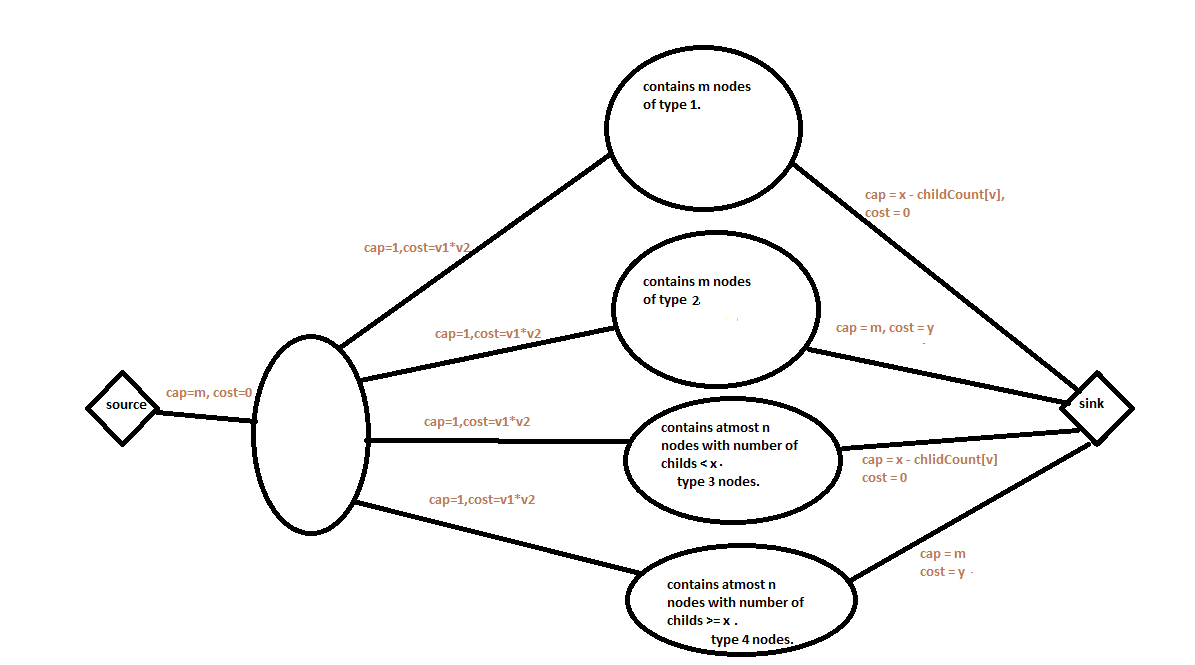
-
Left part of network contains m nodes appearing in the query order. All these vertices are added to source node by capacity of 1 and cost of 0.
There is no other vertex connected to source, Hence maximum flow could be at most m. -
Right part of network has 4 types of vertices given as below.
Type 1- We will have m nodes of query in the given order. These nodes will be connected to the left part
such that right part has appeared earlier in the query than the left part. It will capture the idea of inserting the vertices in the given order of the query. They are connected to sink vertex by capacity of m(max possible flow value) and cost of 0.Type 2- We will m nodes of the query in the given order. These nodes will be connected to the left part
such that right part has appeared earlier in the query than the left part. These nodes are representing
the nodes with > x children.
They are connected to sink vertex by capacity of m(max possible flow value) and cost is equal to y.
Note that this captures the idea of adding new vertex to a vertex with children > x in the already added query nodes. (This is the most important part of our construction.)Type 3- We will have nodes of tree with less than x children in it.
Type 4- We will have nodes of tree with >= x children in it.
-
Left part is connected to right part in following way.
We will be having the edges between left part with cost equal to product of values of two nodes and capacity equal to 1. A flow through the edge from left to right part signifies adding
of some vertex in the query to some of the already added vertices.
Type 1 is connected with sink having capacity of x and cost of 0.
Type 3 is connected with sink having capacity of x - childCount[v] and cost of 0.
So our network above described contains 1(source) + m (left part) + m (type 1) + m (type 2) + n (type 3) + n (type 4) + 1(sink) = 3m + 2n + 2.
Similarly number of edges also contain a factor of n. As n is very large, it will be impossible to solve this network.
Can we somehow reduce then number of vertices and edges, Can we make sure that number of vertices and edges are dependent only on m not on n.
Answer is yes, Here are the crucial observations.
-
Maximum possible flow in the network is m.
-
For type 3 and type 4, We don’t need entire vertices of n, Only considering cheapest m of those will work. This part is obvious to see because the maximum flow in the network is at most m.
So, we will making the following changes to our earlier described network.
In the right part, for type 3, we will consider only least valued m nodes. Similarly for type 4, we will do the same.
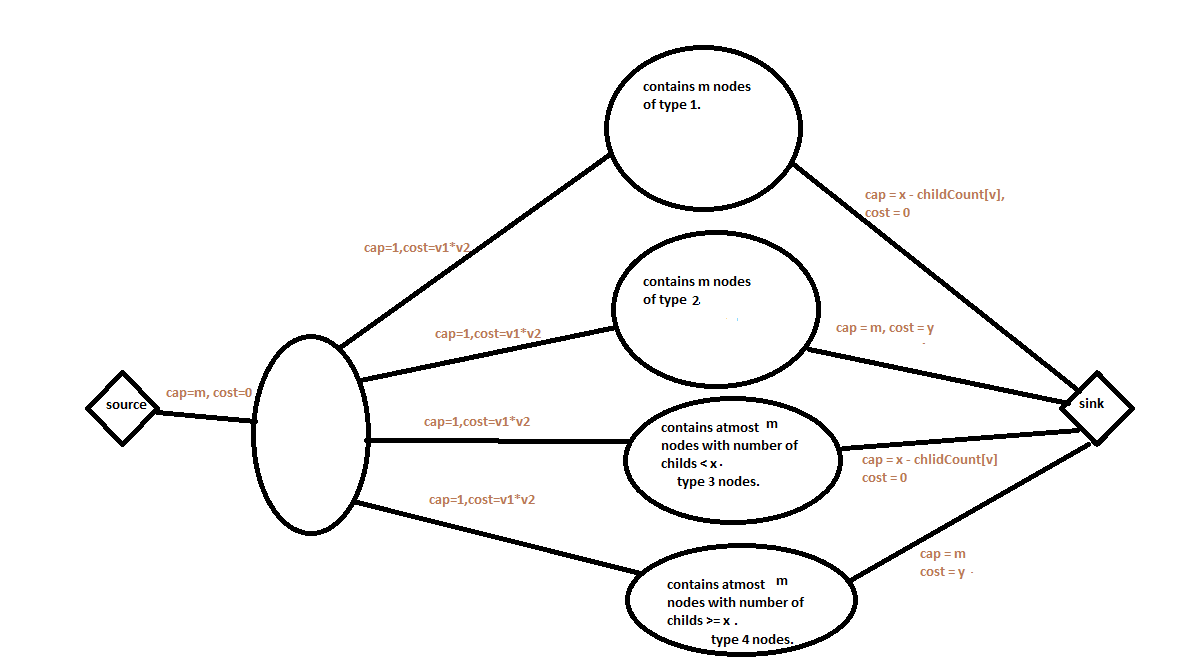
So our network above described contains 1(source) + m (left part) + m (type 1) + m (type 2) + m (type 3) + m (type 4) + 1 (sink) = 5 m + 2.
FURTHER IMPROVEMENTS
We can also do a simple improvement in the network by following way.
In the right part of the network, while considering type 4, we don’t need to take cheapest m vertices, instead we can simply work with the cheapest
vertex itself. If once number of children have become >= x, then it can never be less in subsequent addition of query vertex operations, so instead of taking cheapest m vertices
with children >= x, we can simply add a single vertex having >= x children and with the least value.
See the diagram.
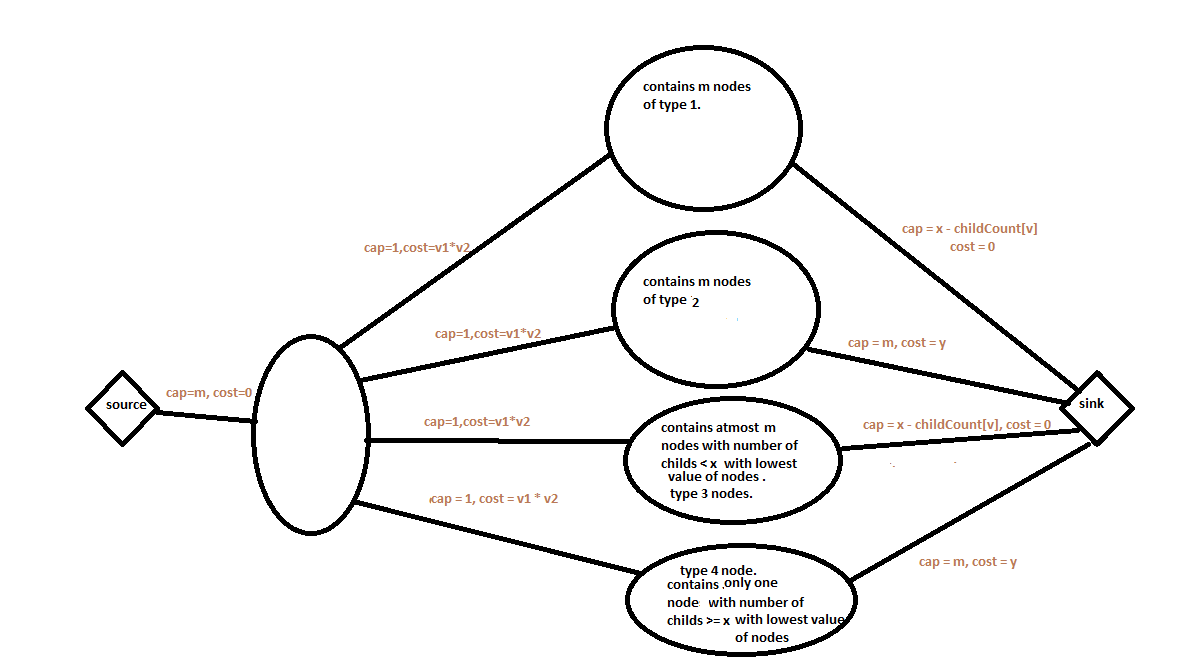
The final network graph has now 1(source) + m (left part) + m (type 1) + m (type 2) + m (type 3) + 1 (type 4) + 1 (sink) = 4m + 3.
HOMEWORK
-
How to create a flow network with 3m vertices instead of 4m. If you can do further improvements, then please share with us in the comments.
Btw you can read tester’s solution for getting the idea of improvement. -
What is the importance of tree here? What will happen if instead of number of children >= x condition, we impose the condition of number
of vertices in the subtree >= x, Can you solve this ? What are the possible issues in dealing with its min cost max flow network. -
When can we apply greedy in these kind of matching problems? Find out arguments to convince yourself in what type of cases greedy should work
and in what kind of cases it wont. What are the possible strategies to prove greedy algorithms for this kind of matching problems.
AUTHOR’S, TESTER’S AND EDITORIALIST’s SOLUTIONS:
Author’s solution
Tester’s solution
Editorialists’s solution