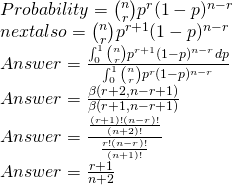I have no idea why it works but I’ll stick some logic to it anyway. Let’s say there have been 0 shots before the current time. Now what is the probability that the next shot will hit the target? Common sense says it should be 1/2. See it is (0+1)/(0+2)
I don’t know why but when you are N shots into the game with R on target. The probability for the next shot to hit comes out to be (R+1)/(N+2).
Maybe someone more experienced in probability can explain it, but in the end that’s what you have to do!
My Solution: CodeChef: Practical coding for everyone
+1
Lets remove the chef bit aside and map the problem into little mathematical scenario.
We have an event happening n times with only two possible outcomes (sucess or failure),
with following assumption made in the problem:
(a) These events are independent and identically distributed (i.i.d)
(From the fact that skill level remains constant)
(b) these events has the probabililty (say p), which is equally likely between 0 and 1.
(From the fact that the probability is uniformly distributed)
Claim: the probability of n+1 event will be sucess given in n event r of them were sucess
is given by (r+1)/(n+2).
Hardcore Mathematical Proof:
Lets denote each of these events to be Bernoulli trails. Lets say X_i be 0 or 1 to denote
the ith trial for sucess or failure.
Lets say
S_n = X_1 + X_2 + ... + X_n
So
According to problem we need to find P(X_n+1=1 | S_n = r).
This was just to give you insight and total proof can be found here(https://jonathanweisberg.org/post/inductive-logic-2/).
Another loose but Smart Proof:
Suppose we have a marble between two wooden planks. we roll it between them and it stopped
due to friction.
Now we roll total n(say 5 for illustration) marbles, r(say 3) of them went on left side of
first ball and rest(2 in this case) right of first ball.
So now if we roll last ball the cases can be
# L L L ** R R
L # L L ** R R
L L # L ** R R
L L L # ** R R
L L L ** # R R
L L L ** R # R
L L L ** R R #
# represent the last ball ** represent the first ball. L and R are the left and right balls
respectively
Now we can easily say that probability of last ball coming out in left is 4/7 as all left
to right arrangements are equally likely a priori.
This whole scenario can be easily mapped with Bernoulli trial of sucess and failure to the
ball landing on left or right, all balls are independent are also taken care.
So in general case probability will be (r+1)/(n+2).I think we cant say that the probability is 1/2 as (a) it is mentioned that probability is uniformly distributed.
(b) otherwise the question will simply be finding value of Binomial Distribution (as the sum of independent Bernoullis is a Binomial)