PROBLEM LINK:
Practice
Contest
Video Editorial
Setter: Rithvik Chatterjee
Tester: Yash Chandnani
Editorialist: Ishmeet Singh Saggu
DIFFICULTY:
Easy
PREREQUISITES:
Games
PROBLEM:
You are given a strip A of length N where A[i]=0 represent a free cell and A[i]=1 represent a blocked cell. Two players Nayeon and Tzuyu play this game and alternate turns.
- Nayeon plays first.
- In the first turn player can go in any free-cell and after that, the player can only go in cells which are free and are adjacent to the current cell.
- If the player visits a free-cell then it is marked as a blocked cell.
- If a player is unable to move to a free cell during her turn, this player loses the game.
Print “Yes” if Nayeon wins else print “No”.
QUICK EXPLANATION:
- In array A we can note that it is in the form of continuous segments of 0's and 1's that is it is in the form of
11110000011111000011110111.... Let us refer to each continuous segment of 0's as zeroSegment. - When all cells are blocked then Nayeon loses.
- When we have only 1 zeroSegment then Nayeon will win only if its length is odd.
- When there are more than 1 zeroSegment then, let us refer to length of largest zeroSegment as L and the length of the second-largest segment as L'. Then Nayeon will win if following conditions are true.
- L is odd.
- L' < \frac{L+1}{2}
EXPLANATION:
When we observe the array A we can note that it is in the form of continuous segments of 0's and 1's that is it is in the form of 11110000011111000011110111.... Let us to each continuous segment of 0's as zeroSegment.
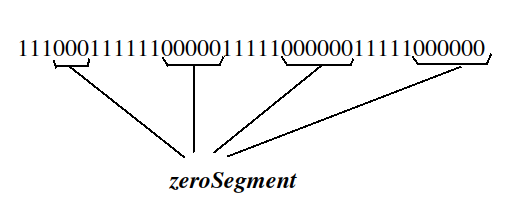
Note that once a player enters a zeroSegment(that enters any free cell belonging to that zeroSegment) it cannot go into any other zeroSegment as there will be blocked cells(or no cell) at the ends of the zeroSegment.
Let us handle the corner test case when there is no zeroSegment, i.e. all cells are blocked then Nayeon cannot make the move hence answer will be No.
Now let us solve the easier version when array A contains only one zeroSegment.
Claim - Optimal move for Nayeon will be to enter the middle cell of the zeroSegment. And if the length L of zeroSegment is odd then Nayeon will win and if its length is even then Tzuyu will win. Note here I am referring the middle cell as the cell which when blocked divides the zeroSegment into two equal-sized zeroSegment of smaller size, so when L is even there is no middle element and when L is odd there is a middle element.
Let us see why choosing the middle cell is the optimal strategy. Consider the length of zeroSegment as length L. Now consider we enter the ith free cell, then marking it as blocked cell after the move there will be 2 zeroSegment. One will be of i-1 free cell to the left and the other will be of L-i cells to the right. When i is not the middle cell or L is even, then the length i-1 and L-i will be unequal. Let us consider that right segment with L-i free cell is longer, then Tzuyu will choose the i+1 box in next turn and there will be no way for Nayeon to enter the free cell or the right segment as i+1 cell is blocked now and the only option for the Nayeon will be to move to the left and enter cells i, i-1, i-2,\dots1 whereas for Tzuyu the only option will be to move to the right and enter cells i+1, i+2, i+3, \dots L, but as we know that the right segment is bigger than left so Nayeon will be out of moves first and will lose. Similarly, you can prove it when the left segment is bigger than the right segment.
So the only case when Nayeon will win is when L is odd and she chooses the middle element as it will divide the zeroSegment into 2 equal segments.
if(numOfZeroSegment == 1) {
if(segmentLen % 2) cout << "Yes\n"; // Only in odd length strip Nayeon can win.
else cout << "No\n";
}
Now when there are more than 1 zeroSegment.
All the condition shown above is true the only thing is that Nayeon will choose the middle element(if possible) of the largest zeroSegment. The only extra condition in this problem is there is a possibility that Nayeon might lose even if the length L of the largest segment is odd. That possibility is :
Suppose L of the largest segment is odd(in all other cases Nayeon will lose as shown above). And the length of second-largest segment L' \geq \frac{L+1}{2}. Because when she chooses the middle element she can make total \frac{L+1}{2} moves (as if Nayeon doesn't choose the middle element thinking that she can make more moves but then she will still lose, as Tzuyu will follow the moves described above) and Tzuyu will enter the leftmost cell of the second-largest zeroSegement will have total moves \geq \frac{L+1}{2}(number of moves of Nayeon) hence Tzuyu will win.
if(numOfZeroSegment > 1) {
if((segmentLenMax % 2) && (segmentLenSecondMax < ((segmentLenMax+1)/2))) {
cout << "Yes\n"; // Nayeon wins
}
else cout << "No\n";
}
TIME COMPLEXITY:
- O(N) in total to find the length of all the zeroSegment.
- In case when the number of zeroSegment > 1. The maximum length and second maximum can be found in 2 for loops of O(N) (you can refer to the editorialist’s code).
- Total time complexity per test case is O(N)
SOLUTIONS:
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
void __print(int x) {cerr << x;}
void __print(long x) {cerr << x;}
void __print(long long x) {cerr << x;}
void __print(unsigned x) {cerr << x;}
void __print(unsigned long x) {cerr << x;}
void __print(unsigned long long x) {cerr << x;}
void __print(float x) {cerr << x;}
void __print(double x) {cerr << x;}
void __print(long double x) {cerr << x;}
void __print(char x) {cerr << '\'' << x << '\'';}
void __print(const char *x) {cerr << '\"' << x << '\"';}
void __print(const string &x) {cerr << '\"' << x << '\"';}
void __print(bool x) {cerr << (x ? "true" : "false");}
template<typename T, typename V>
void __print(const pair<T, V> &x) {cerr << '{'; __print(x.first); cerr << ','; __print(x.second); cerr << '}';}
template<typename T>
void __print(const T &x) {int f = 0; cerr << '{'; for (auto &i: x) cerr << (f++ ? "," : ""), __print(i); cerr << "}";}
void _print() {cerr << "]\n";}
template <typename T, typename... V>
void _print(T t, V... v) {__print(t); if (sizeof...(v)) cerr << ", "; _print(v...);}
#ifndef ONLINE_JUDGE
#define debug(x...) cerr << "[" << #x << "] = ["; _print(x)
#else
#define debug(x...)
#endif
#define rep(i, n) for(int i = 0; i < (n); ++i)
#define repA(i, a, n) for(int i = a; i <= (n); ++i)
#define repD(i, a, n) for(int i = a; i >= (n); --i)
#define trav(a, x) for(auto& a : x)
#define all(x) x.begin(), x.end()
#define sz(x) (int)(x).size()
#define fill(a) memset(a, 0, sizeof (a))
#define fst first
#define snd second
#define mp make_pair
#define pb push_back
typedef long double ld;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
void pre(){
}
int a[300009];
ll sum = 0;
void solve(){
int n=readIntLn(2,3e5);
rep(i,n-1){
a[i] = readIntSp(0,1);
}
a[n-1] = readIntLn(0,1);
assert(a[0]==1);
assert(a[n-1]==1);
sum+=n;
vi v;
int cnt =0;
rep(i,n){
if(a[i]==1) v.pb(cnt),cnt=0;
else cnt++;
}
sort(all(v));
reverse(all(v));
if(sz(v)==1){
if(v[0]%2==1) cout<<"Yes\n";
else cout<<"No\n";
}
else{
if(v[0]%2==1&&(v[0]+1)/2>v[1]) cout<<"Yes\n";
else cout<<"No\n";
}
}
int main() {
cin.sync_with_stdio(0); cin.tie(0);
cin.exceptions(cin.failbit);
pre();
int n=readIntLn(1,40000);
rep(i,n) solve();
assert(getchar()==EOF);
assert(sum<=1e6);
return 0;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
void solveTestCase() {
int N;
cin >> N;
vector<int> A(N), zeroSegmentLen;
for(int i = 0; i < N; i ++) {
cin >> A[i];
}
for(int i = 0; i < N; i ++) {
if(A[i]) continue;
int ptr = i;
while((ptr+1 < N) && (A[ptr+1] == 0)) {
ptr ++;
}
zeroSegmentLen.push_back(ptr-i+1);
i = ptr;
}
if(zeroSegmentLen.size() == 0) { // when all cells are blocked.
cout << "No\n";
}
else if(zeroSegmentLen.size() == 1) {
if(zeroSegmentLen[0] % 2) cout << "Yes\n"; // only in odd length strip Nayeon can win.
else cout << "No\n";
}
else {
int maxLen = 0, id = -1;
int M = zeroSegmentLen.size();
for(int i = 0; i < M; i ++) {
if(maxLen < zeroSegmentLen[i]) {
maxLen = zeroSegmentLen[i];
id = i;
}
}
swap(zeroSegmentLen[0], zeroSegmentLen[id]);
maxLen = 0, id = -1;
for(int i = 1; i < M; i ++) {
if(maxLen < zeroSegmentLen[i]) {
maxLen = zeroSegmentLen[i];
id = i;
}
}
swap(zeroSegmentLen[1], zeroSegmentLen[id]);
// By doing above operation we get maximum at index 0 and second maximum at index 1.
if((zeroSegmentLen[0] % 2) && (zeroSegmentLen[1] <= ((zeroSegmentLen[0]-1)/2))) {
cout << "Yes\n";
}
else cout << "No\n";
}
}
int main() {
ios_base::sync_with_stdio(0); // fast IO
cin.tie(0);
cout.tie(0);
int testCase;
cin >> testCase;
for(int i = 1; i <= testCase; i ++) {
solveTestCase();
}
}
Video Editorial
Feel free to share your approach. In case of any doubt or anything is unclear please ask it in the comment section. Any suggestions are welcomed. ![]()

 )
)




 ).
).
