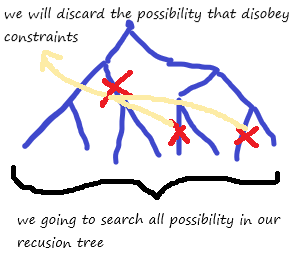
Backtracking is a concept to build a solution using recursion,going through all states and rejecting the state which did not satisfy the constraints.
for understanding we will solve problem name:
Generate all N matched parentheses.
INPUT is :Integer N
OUTPUT is :string of parentheses “(” or “)”…the string should be balanced.
By BALANCED I mean(number of “(” open== number of “)” closing brackets)
So for input N:::
N=1 output is [" () "]
{note 1: opening should be before closing}
N=2 output is [ " (()) “,” ()() "]
{note 2: we have to print all possible solution permutation}
N=3 output is [" ((())) “,” (())() “,” ()()() ", " (()()) “,”()(()()) "]
The three key to recursion
1. Our Choice
{either use ( or ) }
2.Our constraints
{we can not use “)” before “(”}
3:Our Goal
{total 2*N character should be used N ->" ( "+ N -> “)” }
now we move step by step to solve the problem for N=3

When the number of open “(“ bracket is zero we start decreasing count of closing brackets “)” or when open < close
We gonna approach by taking input N and using a recursive function Back_track() with Parameter:
Back_track( number of “(” opening bracket
, number of* “)” closing bracket ,
Empty string which will be filled in each recursion step with either ( or )
vector of string to store the filled strings )**
:::::::::::::::::::CODE:::::::::::::::::::::::::::::::::
class Solution {
public:
void Back_track(int open,int close,string& bracket,vector&v){
if(open==0 && close==0)
{
v.push_back(bracket);
return;
}
if(open>0){
Back_track(open-1, close, bracket + ’(‘ , v );
}
if(open<close){
Back_track(open , close-1 , bracket + ’)’ , v );
}} vector<string> generateParenthesis(int n) { string bracket=””; int open=n,close=n; vector<string>v; Back_track(open,close,bracket,v); return v; } };
