PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Praveen Dhinwa
Tester: Teja Vardhan Reddy
Editorialist: Taranpreet Singh
DIFFICULTY:
Simple
PREREQUISITES:
Observations.
PROBLEM:
Given a garland represented by string S consisting of two colored flowers Red and Blue, determine, whether we can attain a beautiful garland, defined as a garland having no two consecutive flowers of the same color, by applying the following operation at most once.
Make two cuts on garland to obtain two parts, reverse one and join it back.
SUPER QUICK EXPLANATION
- Only even length garlands with the same number of red and blue flowers have the possibility of being a part of beautiful garland, except garland of length 1.
- Such garland is beautiful, if the number of positions having current character same as next character, is either zero or two.
EXPLANATION
Let us see a beautiful garland first.
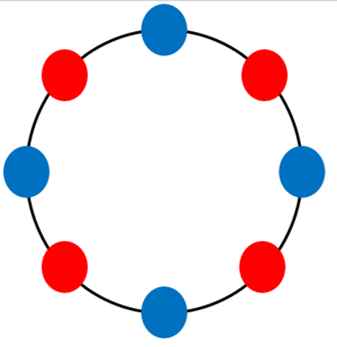
Let us consider a garland of length 1. We know, it has only one flower, so it can never have two consecutive flowers of the same color, hence, is a beautiful garland. We answer yes in this case.
Now, we have garland length \geq 2.
Now, we need to end up with a beautiful garland, which, we can notice, has the same number of red and blue colored flowers. Hence, the garland, which does not have the same number of flowers can never end up as a beautiful garland, even after performing operations.
This way, all garlands we are left with are the garlands of even length (simple to prove) having the same number of flowers of both colors.
First of all, check if the garland is already beautiful and report if it is. Now, we are left with a non-beautiful garland and we have to make a cut, trying to make it beautiful.
Let us understand the consequence of performing the operation. See, we make the cut, reverse a string, and attach it back. Except for border flowers of both pieces of garland, the rest of the flowers continue to have same adjacent flowers as before.
Consider an example RRGGRRGG. We make first cut between first and second flower while the second cut between seventh and eighth flower. The resultant garland becomes RGRRGGRG. We see, that only pairs of positions around both cuts are affected by the operation.
Hence, if we call a pair of adjacent same-colored flowers as mismatch positions, then, we can prove, that we can remove exactly two mismatches using one swap.
See, since only the two pairs of positions enclosing either of the cut are affected by a cut, we cannot remove more than 2 mismatch positions using one operation.
This way, the solution is just to count the number of mismatch positions in garland, and we can make the garland beautiful, if there are either zero or exactly two mismatch positions, after handling the case of garland consisting of a single flower.
Exercise
Prove that the number of mismatch positions in an even length garland having the same number of both colored flowers, cannot have an odd number of mismatch positions.
Time Complexity
Time complexity is O(|S|) since we iterate over the string.
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Editorialist’s solution
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()


