Please provide the editorial of question The Best Box
Let’s understand this question in a different way 
Johnny needs to make a rectangular box for his physics class project, Let’s understand it into different way… His teacher slapped him and told … “Go to your home, and make project for me to find the largest volume of the box that you could make…”
Johny asked “How can i do that madam?”
Madam: You have to make a rectangular box. You’ve given P cm of wire and S cm2 of special paper… (Hope so johnny, you know this is an area of paper). You’d have to use all those wire to make 12 edges.
Johnny: 12 edges? I don’t understand madam?..
Madam: SLAPPED!! … Fool… look at this picture…
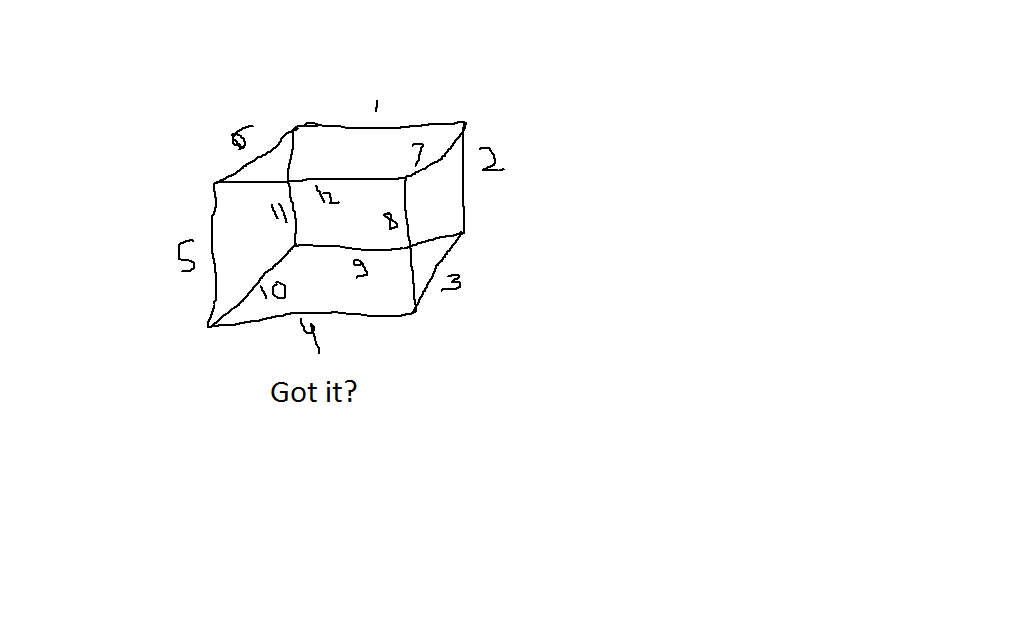
Johnny: Okay madam… Please continue…
Madam: And paper for six sides…
Johnny: And what is this madam?
Madam: Again SLAPPED!!.. Look at this picture…
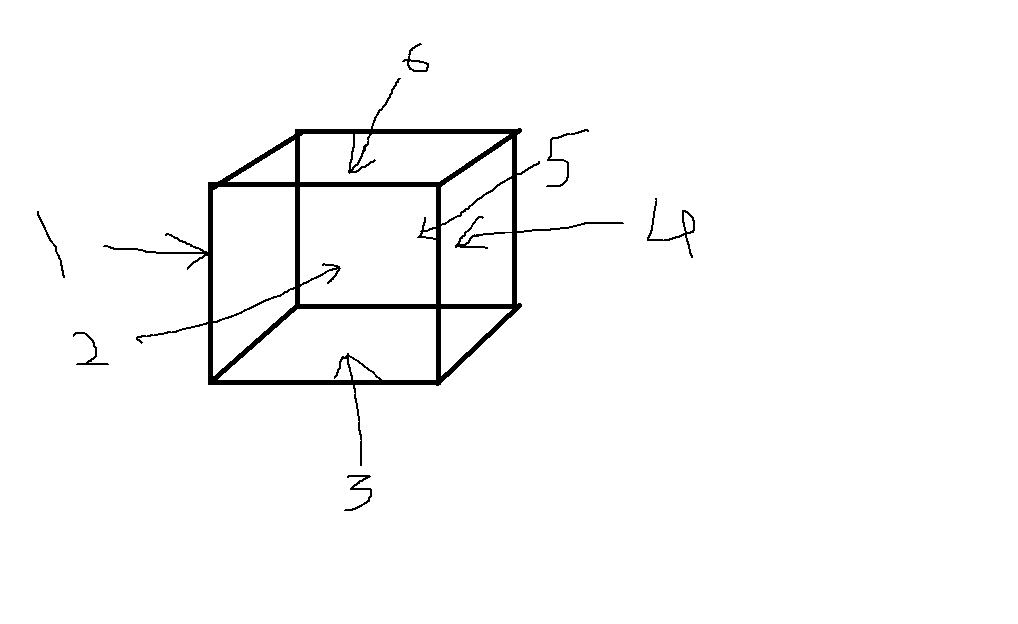
Johnny: got it… please continue…
Madam: Now, you’ve to find the largest volume of the Box.
Madam: Do you know volume of box mean?
Madam: It’s okay … look at this pic…
HOPE YOU FIND THE BEST ANSWER!!.. 
This problem is purely based on mathematics,just brush up your concepts of maxima and minima and then try to derive a formula. Hope it helps!
The volume V=lbh
Now using 4(l+b+h)=P and 2(lb+bh+hl)=S
Convert the above formula of V in terms of only h so that we can differentiate it and then get the value of h for where the volume will maximize or minimize.
If you make the right subsitutions the volume will come out to be equal to (S/2-h(P/4-h))*h.
Differentiate the above and then you will get two values of h. One will be for maximum value and other will be for minimum value. Use a if statement to find out which one is which.
Also use double which will have better precision.
Hope this helps:).
Thanks