PROBLEM LINK:
Author: Kamil Debowski
Primary Tester: Marek Sokołowski
Secondary Tester: Praveen Dhinwa
Editorialist: Praveen Dhinwa
DIFFICULTY:
med-hard
PREREQUISITES:
geometry, binary serach
PROBLEM
There are n points in 2-D plane. No two points have same coordinates and no three points are collinear. Consider all the triangles that have their area less than or equal to K/2. Find out the maximum area among these triangles.
SOLUTION
Start with brute force solution
We can iterate over all the triplets of points and find the area of the triangle made by the triplet and take the best area that is less than or equal to K/2. This takes \mathcal{O}(n^3) time which won’t pass for n = 3000. Can we do better?
How could we have done better?
Suppose that you have fixed the base of triangle by selecting a pair of points among these n points. You want to find the other point of the triangle in such a way that the height of the triangle is as large as possible and its area is less than or equal to K/2. You want to do this better than just iterating over the remaining n-2 points and trying each point as the third point of the triangle. Suppose that you know the ordering of the points w.r.t. their heights with the base (ie. the perpendicular distance of the points from the base considered as a line), can you do it faster? For sake of simplicity, assume that if the point lies above this base, then its height is positive, and negative otherwise. This makes it easy for you to do a binary search for the desired area triangle with this base. It would be very nice if we could maintain this sorted order of points while going through each of the \mathcal{O}(n^2) possible bases of the triangle, in time better than re-computing this order each time in \mathcal{O}(n).
Maintain sorted order of points while going through the slopes.
Imagine we have a line, which is horizontal initially, that slowly rotates in counter clockwise direction. We maintain the points ordered w.r.t the distances from this line. When this line is parallel to a line joining some pair of points, then these points will be at an equal distance from our line and afterwards their order of distances is changed. Next few paragraphs formalize this intuition.
Let us say that you have all the \binom{n}{2} slopes sorted in counter clockwise order w.r.t their slope (i.e. angle with x axis).
Let us start with the smallest positive slope. We maintain the sorted order of the n points w.r.t height (distance) from this slope in a list L. We do this by just calculating the distances for each point and then sorting. (You can observe that this order will actually be the non-decreasing order of their y coordinates. Proving this is left as a simple exercise)
Now we go to the next slope in counter clockwise order. How does it changes the list L? Let this slope be made by points p_i, p_j.
Claim: The only change in the list L, to maintain the right order of points wrt to distances from the slope (p_i, p_j) will be as follows: Let the previous slope be q_i, q_j. Only the points q_i and q_j will change their order in list L. All other points will retain their order.
Proof:
Let us consider the slope which was considered before the slope (q_i, q_j). While considering that slope, we can see that q_i appears before q_j in list L. While considering the slope (q_i, q_j), both q_i, q_j are at the same height. After the slope (q_i, q_j), the new slope p_i, p_j has higher angle. So, point q_i will no longer be appearing before q_j. They will be changing their order.
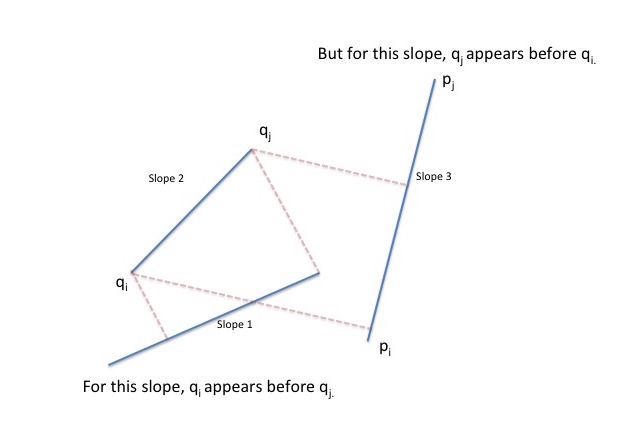
Now the only part that remains to understand is that none of the points other than q_i and q_j will be changing their order in L. You can prove that two points will only be changing their order if they encounter a slope equal to them, and the next slope to be considered is higher than the slope made by these two points.
Final solution summarized
We iterate over the slopes in sorted order w.r.t their slope. We maintain the list L of points sorted w.r.t their height from the slope. For each slope, we do two binary searches to find the maximum area triangle with area less than or equal to K/2, and also update the list L by making one swap.
There are total \mathcal{O}(n^2) slopes and for each slope we do two binary search operations in \mathcal{O}(log n) time. Thus the total time complexity will be \mathcal{O}(n^2 \, log n).
Pseudo Code
Let S = list of slopes made by pair of points {p_i, p_j} such i < j
sort S by increasing order of slope (in counterclockwise order)
Let L = list maintaining the order of points w.r.t height from the slope.
Initially L will be sorted by distances from the smallest slope line..
for each slope s in S:
let p, q be the points for slope s.
// Binary search in X for max area a such that a <= K/2.
// Binary search in X for max area -a <= K/2. Here we are assuming that height can be negative too, so the area can be negative too. You can think of the area as signed area.
Let i be the index/position of p in X.
Similarly, let j be the index/position of q in X. //j will actually be i+1. This is left as an exercise.
swap L[i], L[j].