PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author: fmota
Tester: smelskiy
Editorialist: fmota
DIFFICULTY:
Medium-Hard
PREREQUISITES:
Data structures, queue, stack, dynamic programming
PROBLEM:
Given an empty grid, it’s necessary to handle 3 different query types, addition of a new line, where each cell has its own color (0 or 1), in the bottom of the grid, removal of the topmost line and counting of number of ways going from one of the topmost cells in the grid to one of the bottommost only passing by cells of the same color.
QUICK EXPLANATION:
The problem can be interpreted as requiring a modified queue (push, pop & number of paths). If the problem required a modified stack (push, pop & number of paths), it could be solved with dynamic programming, keeping for each element in the stack, the number of ways to go to the bottom of the stack, ending in any of the possible bottom cells, this would require O(N^2) for push operation and O(1) for pop and query. There is a trick that allows to emulate a queue using two stacks (Method 2 in link), with this trick it’s possible to emulate a modified queue with 2 modified stacks, now the push and pop would have O(N^2) amortized complexity, the query requires now merging the results of both modified stacks, which can be done in O(N), using the fixed columns.
EXPLANATION:
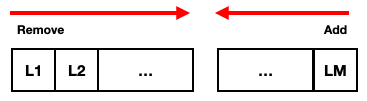
The first thing to do in this problem is to see what the add and remove operation mean, looking to the following image we can have a better idea:

In the image, the grid is rotated and represented as an array of lines, L1 represents the topmost line of the grid and LN the bottommost. Based on the image, we can see that the operations are similar to the operations present in a queue, this is an important detail to solve the problem.
Now, let’s work on calculating the number of ways, first let’s try to solve the problem disregarding add, remove operations and considering a non empty grid. So, there will be many path operations, but no add/remove operation. This version of the problem can be solved with dynamic programming, to solve all the queries we only need to calculate L_{cd}, where L_{cd} is the number of ways going from the topmost line in the c-th column going to the bottommost line in the d-th column. If the grid only has one line, L_{cd} = [c == d], because one cell can only reach itself on the same line. If the grid has M \geq 2 lines, we can consider L_{cd}^i as the result for the first i lines, knowing L_{cd}^i we can compute L_{cd}^{i+1} in O(N^2) complexity. So the overall process will take O(M*N^2), this method could be used in each query of the first subtask and solve it completely.
So far, there are no advances in how to handle add/remove operations, if the operations were stack like ones, the problem could be solved in O(Q * N^2) complexity, consider the following image:

The image follows the same format of the first image shown, but instead it considers the operations as if its stack like ones. considering the process of calculating the number of paths previously described we could store on the stack all L_{cd}^i and solve path/remove operations in O(1) and calculate the new L_{cd}^M in O(N^2) in the add operation.
There is an interesting trick that allows to emulate a queue with 2 stacks (Method 2 in link). Knowing this trick, the full problem can be solved, to be clearer, consider the following image:
Pseudo code
stack a, b
add(element):
push(b, element)
remove():
if empty(a):
while not empty(b):
element = top(b)
pop(b)
push(a, element)
pop(a)
In the trick, the queue is partitioned in two stacks, it’s only necessary stack operations and it’s possible to handle queue operations, as an element in the worst case will pass by the two stacks and going to be removed, the overall complexity to process T operations is O(T).
Using the trick of 2 stacks, the queue problem can be reduced to solving 2 times the problem in the stack, using the method previously described to handle stack problem, it’s possible to keep the information of paths in the form La_{cd} and Lb_{cd} representing the number of paths for each stack. This lead to O(N^2) amortized complexity in add/remove operations. The only remaining problem is how to calculate the overall result, taking into consideration both stacks. One way is to only calculate it when we receive a path query, using both c and d fixed by the query, we only have to consider all of the N possible points that connect one stack to the other, so the path query can be solved in O(N).
Some solutions that aren’t optmized for IO or aren’t optimized for memory maybe have problem to pass all test cases, the TL is tight, the reason is to cut off some optimized D&C solutions, but unhappily some D&C solutions were able to pass.
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
using namespace std;
template<typename T = int> vector<T> create(size_t n){ return vector<T>(n); }
template<typename T, typename... Args> auto create(size_t n, Args... args){ return vector<decltype(create<T>(args...))>(n, create<T>(args...)); }
const int mod = 1'000'000'007;
const int maxq = 300000, maxn = 20;
int w[2][maxq][maxn][maxn], stk[2];
string p[2][maxq];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int N, C, Q;
cin >> N >> Q;
auto upd_back = [&](int id){
int n = stk[id];
if(n >= 2){
for(int i = 0; i < N; i++){
for(int j = 0; j < N; j++) w[id][n - 1][i][j] = 0;
for(int j = i-1; j <= i+1; j++){
if(j < 0 || j >= N) continue;
if(p[id][n - 1][i] != p[id][n - 2][j]) continue;
for(int k = 0; k < N; k++){
w[id][n - 1][i][k] += w[id][n - 2][j][k];
if(w[id][n - 1][i][k] >= mod) w[id][n - 1][i][k] -= mod;
}
}
}
} else if(n == 1){
for(int i = 0; i < N; i++) for(int j = 0; j < N; j++) w[id][0][i][j] = i == j;
}
};
while(Q--){
string ty; cin >> ty;
if(ty[0] == 'a'){
string s; cin >> s;
p[1][stk[1]++] = s;
upd_back(1);
} else if(ty[0] == 'r'){
if(stk[0] == 0){
while(stk[1]){
p[0][stk[0]++] = p[1][--stk[1]];
upd_back(0);
}
}
stk[0]--;
} else {
int i, j; cin >> i >> j; i--; j--;
if(stk[1] == 0){
cout << w[0][stk[0]-1][i][j] << '\n';
} else if(stk[0] == 0){
cout << w[1][stk[1]-1][j][i] << '\n';
} else {
int ans = 0;
for(int k = 0; k < N; k++){
for(int k2 = k - 1; k2 <= k + 1; k2++){
if(k2 < 0 || k2 >= N) continue;
if(p[0][0][k] != p[1][0][k2]) continue;
if(!w[0][stk[0] - 1][i][k]) continue;
if(!w[1][stk[1] - 1][j][k2]) continue;
ans += (1ll * w[0][stk[0] - 1][i][k] * w[1][stk[1] - 1][j][k2]) % mod;
if(ans >= mod) ans -= mod;
}
}
cout << ans << '\n';
}
}
}
return 0;
}
Tester's solution
/*
O(Q * N * N)
*/
#include <iostream>
#include <string>
#include <cstring>
#include <cassert>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <map>
using namespace std;
const int N = 300005;
const int MD = 1'000'000'000 + 7;
struct query_t {
int r;
int source, target;
int id;
};
int m, queries;
string ar[N];
int n;
map<pair<int, int>, vector<int> > dpl, dpr;
vector<int> save_l[N], save_r[N];
vector<query_t> q[N];
vector<int> ans;
int left_dp[20][20], right_dp[20][20];
void save_unique(vector<int>& w) {
sort(w.begin(), w.end());
vector<int> nw;
for (int i = 0; i < w.size(); ++i) {
if (!i || w[i] != w[i - 1])
nw.push_back(w[i]);
}
w = nw;
}
void read_queries() {
int l = 1;
string query_type = "";
int x, y;
for (int i = 1; i <= queries; ++i) {
cin >> query_type;
if (query_type == "add") {
cin >> ar[++n];
} else if (query_type == "remove") {
++l;
} else if (query_type == "path") {
cin >> x >> y;
--x; --y;
save_l[l].push_back(x);
save_r[n].push_back(y);
q[l].push_back({n, x, y, (int)ans.size()});
ans.push_back(0);
}
}
for (int i = 1; i <= n; ++i) {
if (!save_l[i].empty())
save_unique(save_l[i]);
if (!save_r[i].empty())
save_unique(save_r[i]);
}
return;
}
void recalc_left_dp(int l, int mid) {
memset(left_dp, 0, sizeof(left_dp));
for (int i = 0; i < m; ++i) {
left_dp[i][i] = 1;
}
vector<int> dp(m, 0);
for (int i : save_l[mid]) {
for (int j = 0; j < m; ++j)
dp[j] = left_dp[j][i];
dpl[{mid, i}] = dp;
}
memset(right_dp, 0, sizeof(right_dp));
for (int i = 0; i < m; ++i)
right_dp[i][i] = 1;
dp.resize(m, 0);
for (int i : save_r[mid]) {
for (int j = 0; j < m; ++j) {
dp[j] = right_dp[j][i];
}
dpr[{mid, i}] = dp;
}
while (mid > l) {
for (int i = 0; i < m; ++i) {
vector<long long> dp(m, 0);
for (int j = 0; j < m; ++j) {
int cur = left_dp[i][j];
if (j && ar[mid][j] == ar[mid - 1][j - 1])
dp[j - 1] += cur;
if (ar[mid][j] == ar[mid - 1][j])
dp[j] += cur;
if (j + 1 < m && ar[mid][j] == ar[mid - 1][j + 1])
dp[j + 1] += cur;
}
for (int j = 0; j < m; ++j) {
left_dp[i][j] = dp[j] % MD;
}
}
--mid;
for (int i : save_l[mid]) {
vector<int> dp(m);
for (int j = 0; j < m; ++j)
dp[j] = left_dp[j][i];
dpl[{mid, i}] = dp;
}
}
return;
}
void push_right(int r) {
for (int i = 0; i < m; ++i) {
vector<long long> dp(m, 0);
for (int j = 0; j < m; ++j) {
int cur = right_dp[i][j];
if (j && ar[r][j] == ar[r + 1][j - 1])
dp[j - 1] += cur;
if (ar[r][j] == ar[r + 1][j])
dp[j] += cur;
if (j + 1 < m && ar[r][j] == ar[r + 1][j + 1])
dp[j + 1] += cur;
}
for (int j = 0; j < m; ++j) {
right_dp[i][j] = dp[j] % MD;
}
}
++r;
for (int i : save_r[r]) {
vector<int> dp(m);
for (int j = 0; j < m; ++j)
dp[j] = right_dp[j][i];
dpr[{r, i}] = dp;
}
return;
}
int solve_query(const vector<int>& lhs, const vector<int>& rhs) {
__int128 result = 0;
for (int i = 0; i < m; ++i) {
result += lhs[i] * 1ll * rhs[i];
}
result %= MD;
return (int)result;
}
void process_queries() {
int mid = -1;
int l = -1, r = -1;
for (int i = 1; i <= n; ++i) {
for (query_t& query : q[i]) {
if (i > mid) {
recalc_left_dp(i, query.r);
l = i;
mid = query.r;
r = query.r;
}
while (r < query.r) {
push_right(r++);
}
ans[query.id] = solve_query(dpl[{i, query.source}],
dpr[{query.r, query.target}]);
}
}
}
int main(int argc, const char * argv[]) {
#ifdef __APPLE__
freopen("/Users/danya.smelskiy/Documents/Danya/Resources/input.txt","r",stdin);
#endif
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> m >> queries;
read_queries();
process_queries();
for (int i = 0; i < ans.size(); ++i) {
cout << ans[i] << '\n';
}
return 0;
}
