PROBLEM LINK:
Author: Trung Nguyen
Tester: Hanlin Ren
Editorialist: Hanlin Ren
DIFFICULTY:
MEDIUM
PREREQUISITES:
Trigonometry, Fast Matrix Exponentiation, Modular Inverse
PROBLEM:
A clock has a minute hand which goes x angle per second. The minute hand has length l and the center of clock has coordinate (0,0). Initially, the other endpoint is at coordinate (0,l), and after 1 second its y-coordinate becomes d. Given l,d,t(x is unknown), calculate the y-coordinate of this endpoint after t seconds.
QUICK EXPLANATION:
By the problem statement we have \cos(x)=d/l, and the final answer is \cos(tx)\cdot l. So we only need to compute \cos(tx). There is a formula computing \cos(nx):
and we can use fast matrix exponentiation to compute \cos(tx) in O(\log t) time.
EXPLANATION:
A note to modular arithmetic
Click to view
During the contest, a lot of people asked problems on the output section, in particular related to “modular inverse”. So let’s answer them here.
Let m,a,b be integers. a is the modular inverse of b in modulo m if (a\cdot b)\equiv 1\pmod m. For example, 8 is the modular inverse of 7 in modulo 11 since
We can prove that, in modulo m, a has an inverse if and only if \gcd(m,a)=1. (\gcd(7,11)=1 in above case.) To find the modulo inverse of a in modulo m, one solves the following equation
by the Extended Euclidean Algorithm. Note that x,y are variables to solve; x is the modulo inverse of a. The modular inverse, if exists, is unique in modulo m. (You may say 19 is also a modular inverse of 7 in modulo 11, but 19 and 8 are equivalent.)
If m is a prime(in our problem, m=10^9+7 is a prime), then every integer 1\le a < m has a modular inverse, and let’s denote it as a^{-1}. The inverse can be computed in another way:
by Fermat’s little theorem, it’s simply (a^{m-2}\bmod m).
For a rational number \frac{p}{q}, if \gcd(q,m)=1, then it’s equivalent to p\cdot q^{-1} in modulo m. For example, \frac{2}{3}\equiv 2\cdot 3^{-1}\equiv 2\cdot 333333336\equiv 666666672\pmod {10^9+7}.
Now, in modulo m where m is a prime, we can manipulate every rational number as if it was an integer. For example, let’s compute \cos(x)=d/l and \sin^2(x)=1-\cos^2(x). The corresponding Python code is:
mod = 1000000007
cos_x = (d * pow(l, mod - 2, mod)) % mod
sqr_sin_x = (1 - cos_x * cos_x) % mod
and no manipulation of fractions is involved. Everything is just elements in \mathbb{Z}/(10^9+7)\mathbb{Z}.
(Note: \sin(x) can’t be computed even if \sin^2(x) can. This is because \sin(x) might not be rational. In this case, \sin^2(x) is a quadratic non-residue modulo 10^9+7.)
(Note 2: if you use languages such as C++, beware of overflow and underflow. For example, multiplying a and b should be written as (1ll*a*b)%mod rather than (a*b)%mod; the correct way to subtract b from a is (a-b+mod)%mod rather than (a-b)%mod. Think about the reasons yourself.)
Setter’s Solution
First notice that x is given by \cos(x)=d/l. To see this, consider the following figure which illustrates the problem statement: OA and OB are the position of minute hand initially and after 1 seconds, respectively.
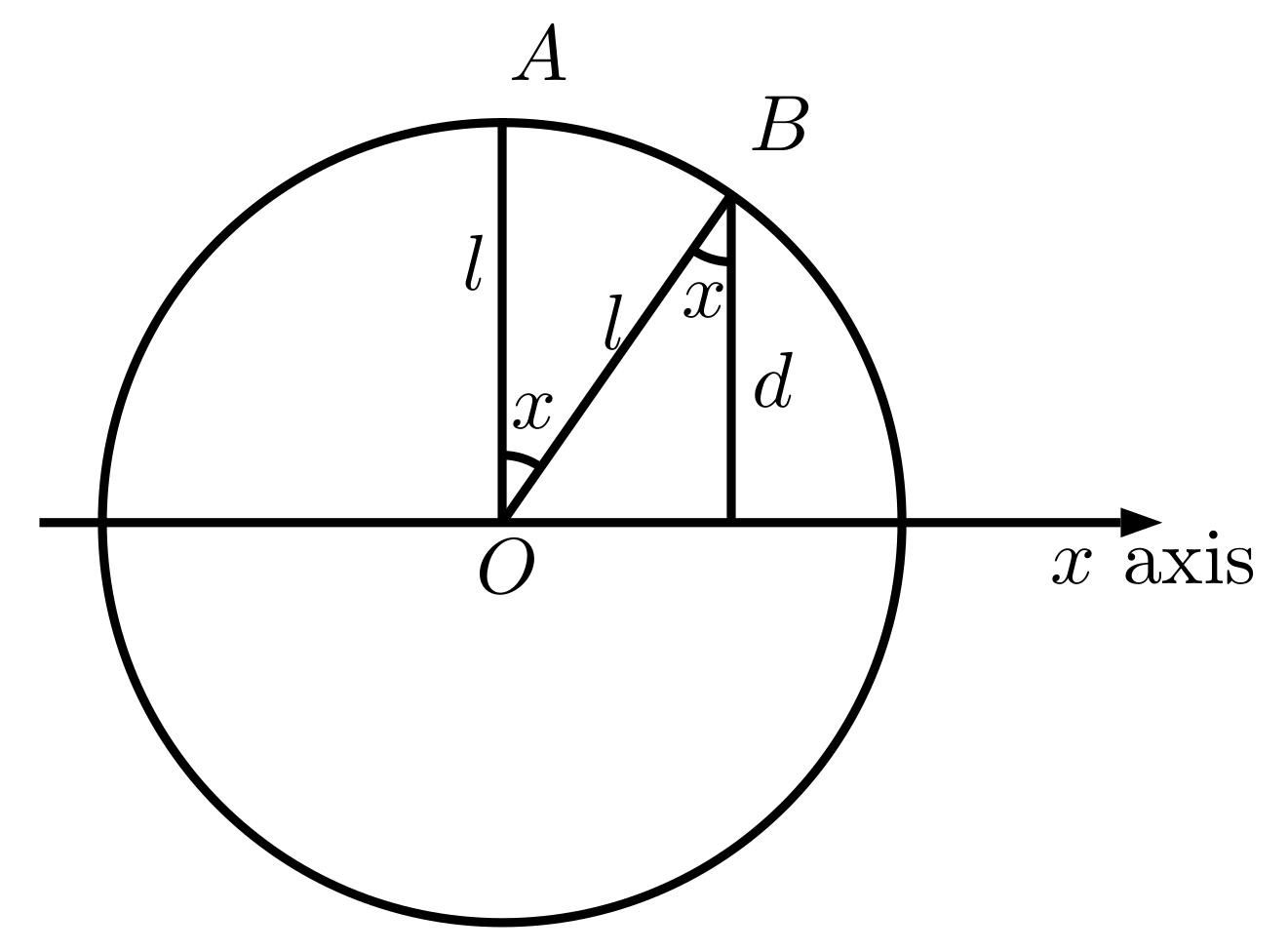
And the answer after t seconds is \cos(tx)\cdot l. Therefore, our actual task is: given \cos(x) and integer t, compute \cos(tx).
Notice the following formula:
that means we can write \cos(tx) in a matrix-multiplication form:
and therefore
Thus we can compute \cos(tx) by fast matrix exponentiation in O(\log t) time.
Tester’s Solution
Again, we’re given \cos(x) and integer t and we want to compute \cos(tx). But what if we don’t know formula (*)? We can use the following (better-known) formula:
All numbers we come across will be in the form a+b\sin(x). Although we don’t know \sin(x), we can represent such a number as (a,b). Therefore we can define +,-,\times on these numbers:
We can write a recursive procedure \mathrm{Solve}(t) for computing the pair (\cos(tx),\sin(tx)).
- If t=1, we return \cos(tx)=(\cos(x),0) and \sin(tx)=(0,1);
- If t is odd, then we find (\cos((t-1)x),\sin((t-1)x)) by calling \mathrm{Solve}(t-1), and (\cos(tx),\sin(tx)) can be computed by formula (1) and (2);
- If t is even, then we call \mathrm{Solve}(\frac{t}{2}) to find (\cos(\frac{t}{2}x),\sin(\frac{t}{2}x)), and (\cos(tx),\sin(tx)) can be computed similarly.
This procedure runs in O(\log t) time since every two steps decrease t by half.
Suppose we’ve computed \cos(tx)=(a,b). b must be equal to 0 since it’s possible to represent \cos(tx) by only \cos(x) terms. Therefore \cos(tx)=a and we’re done.
On formula (*)
How to prove formula (*)? In fact I don’t know, but one might look into this page for answer. The Chebyshev polynomial of the first kind is defined as T_0(x)=1, T_1(x)=x and T_{n+1}(x)=2xT_n(x)-T_{n-1}(x). It can be proved that T_n(\cos(x))=\cos(nx), which directly implies formula (*).
ALTERNATIVE SOLUTION:
Please feel free to share your approach ![]()
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.