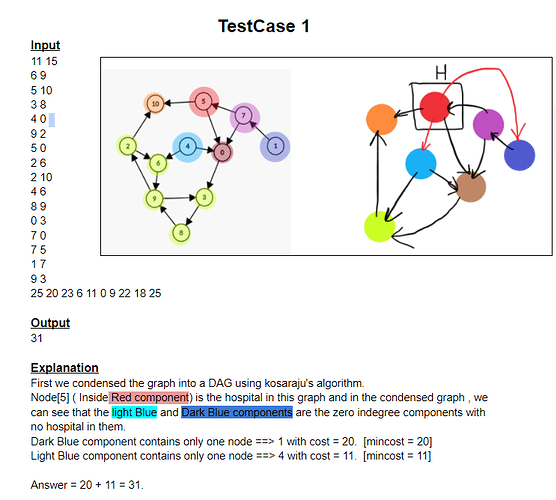
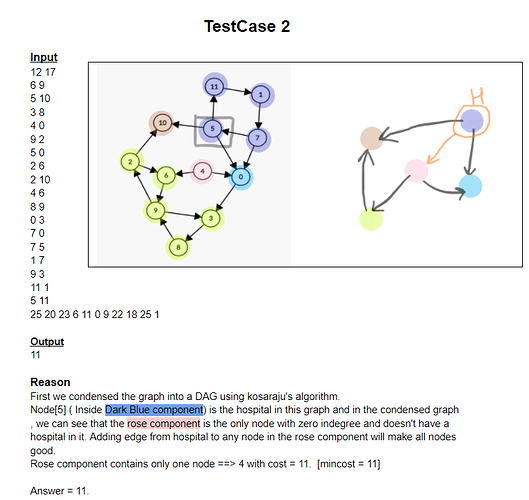
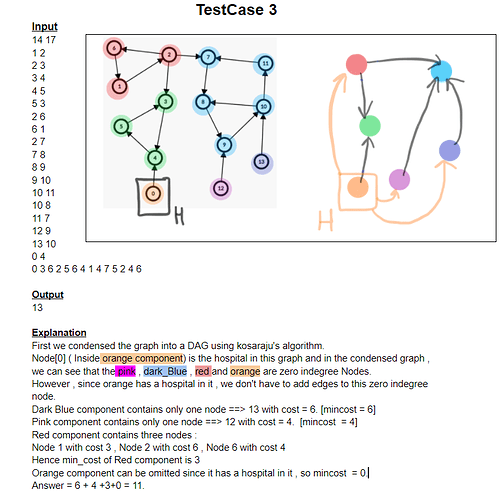
PROBLEM LINK:
Problemset - CAGHS
AC-RUN Contest Link
Author: Hardik, Ganesh , Shobit.
Tester: Hardik, Ganesh , Shobit.
Editorialist: Shobit.
DIFFICULTY:
MEDIUM
PREREQUISITES:
Graphs , DFS , Strongly Connected Components (Kosarajus Algorithm) , Topological Sort
PROBLEM:
Basically , we have been given a directed graph and we have to add edges into this graph such that every node is reachable from at least one of the hospital nodes. Each edge added from u to v costs C(v) . We have to add edges optimally so that total cost can be minimized.
EXPLANATION:
-
It’s always optimal to add the edges directly from some hospital to a node which is Bad.
-
If there are two nodes u , v. If u is good and there is an edge from u to v , then v is also good. Similarly there will be components of such Bad nodes as well.
-
Let’s assume for now that the given graph is always a DAG
- In a DAG there will always exist some zero indegree nodes and these will be the nodes which don’t have a direct path from some hospital unless they are hospital themselves.
- If all the zero indegree nodes in the DAG are hospitals , then all the nodes in the graph will become good as there will always exist a path from some zero indegree node to any particular node. ( Basic idea of topological sort in DAG).
- Hence to solve a graph which is DAG , just add edges from some hospital to all the zero indegree nodes which are not a hospital. This will automatically ensure all the remaining nodes become good.
-
Now how will we approach in case of a general directed graph ?
- Apply kosaraju’s algorithm ( dfs on reverse graph in reverse order of finishing time) to condense the graph into its strongly connected components. In a strongly connected component , each node will be reachable from u to v as well v to u.
- A SCC graph will always be a DAG. ( The most significant point ). Since , there will never be a cyclic loop in the condensed graph of a SCC.
- Since it’s a DAG , we can solve it using the idea above for dealing with DAG.
- For each component keep track of its indegree.
- For each component keep track if there is a hospital in it.
- Keep track of the min_cost node in each component.
- Answer = sum of all the min_cost( components ) which have indegree zero and does not have hospital in it.
- We can treat the nodes analogously as if we have been given DAG as input.
- Components containing hospitals is a hospital node. Otherwise it’s a normal landmark , with cost = Minimum(cost all nodes in this component).
SOLUTIONS:
Editorialist's Solution
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define int ll
#define debug(v) cout << ">>" << #v << ':' << v << endl;
#define endl "\n"
#define pb push_back
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define umap unordered_map
#define pii pair<int , int>
#define all(v) v.begin() , v.end()
#define ld long double
#define min3(a,b,cost) min(a,min(b,cost))
#define min4(a,b,cost,d ) min(a , min(b , min(cost,d)))
#define max3(a,b,cost) max(a , max(b,cost))
#define max4(a,b,cost,d) max(max(a,b) , max(cost,d))
#define vi vector<int>
#define x first
#define y second
#define dbg(a,b) cout<<a<<" "<<b<<endl;
#define mk make_pair
#define rep(i,j,n) for(int (i)=(j) ; i<(n) ; i++)
#define pq priority_queue
#define mn(v) *min_element(all(v))
#define mx(v) *max_element(all(v));
void reader()
{
#ifndef ONLINE_JUDGE
// for getting input from input.txt
freopen("input.txt", "r", stdin);
freopen("output.txt" , "w" , stdout);
#endif
}
const int MOD = 1e6;
const int N = 2e5+10;
const int inf = 1e18;
///////////////////////////////////////template ends here :
int n , m;
vector<int> adj[N] , g[N]; // Adj is the normal graph and G is reversed graph.
bool vis[N];
stack<int> path; // stores the nodes as per finishing time of dfs in given graph.
int h[N]; // Stores the costs of each node , zero if hospital.
int C[N]; // stores component id of each node in condensed graph.
int cnt=0; // for keeping track of number of components in condensed graph.
void dfs( int u )
{
vis[u] = true;
for(auto i : adj[u])
{
if(!vis[i])dfs(i);
}
path.push(u); // stores as per the finishing time.
}
// Run dfs on reversed graph in reverse order of finishing time obtained in dfs on normal graph.
void scc( int u)
{
vis[u] = true;
C[u] = cnt;
for(auto i : g[u])
{
if(!vis[i])scc(i);
}
}
void solve()
{
cin>>n>>m;
for(int i=0 ; i<m ; i++)
{
int u , v;
cin>>u>>v;
adj[u].pb(v); //Normal graph.
g[v].pb(u); // Reversed graph.
}
for(int i=0 ; i<n ; i++)cin>>h[i]; // Node_cost , zero if hospital.
for(int i=0 ; i<n ; i++) // DFS on given graph.
{
if(vis[i] == 0)dfs(i);
}
for(int i=0 ; i<n ; i++)vis[i] = 0;
// Kosarajus Algorithm of finding SCC.
while(path.size() > 0) // dfs on reverse graph with obtained finishing times.
{
if(!vis[path.top()] )
{
scc(path.top());
cnt++;
}
path.pop();
}
// After obtaining strongly connected components :-
vector<int> indegree(cnt , 0); //stores indegree of each component
vector<int> has_H(cnt , 0); //stores if there is hospital in a component
vector<int> Min_node(cnt , inf); //stores the min_cost node in each component.
for(int i=0 ; i<n ; i++)
{
if(h[i] == 0) //if there is hospital in component
{
has_H[C[i]] = 1;
}
else //updation of min_cost node of each component.
{
Min_node[C[i]] = min(Min_node[C[i]] , h[i]);
}
for(auto j : adj[i]) //Update indegree if cross component edges exist.
{
if(C[j] != C[i])
indegree[C[j]]++;
}
}
int ans=0;
for(int i=0 ; i<cnt ; i++) // iterate through all components. [ cnt == number of components]
{
// add cost of those components which doesnt have a hospital in them and have indegree 0.
if(indegree[i] == 0 && has_H[i] == 0)
{
ans += Min_node[i];
}
}
cout<<ans<<endl;
// Expected Time complexity O(N+M).
// O(N+M) for first DFS
// O(N+M) for reverse second dfs.
// O(N) for updating component details and finding answer.
}
signed main()
{
IOS
//reader();
solve();
}