PROBLEM LINKS
Author: Abdullah Al Mahmud
Tester: Gerald Agapov
Editorialist: Praveen Reddy Vaka
DIFFICULTY:
cakewalk
PREREQUISITES:
Basic Coordinate Geometry
EXPLANATION
Restated in simple terms the problem asks for the area of the union of rectangles. Let us call the rectangles R1 and R2. A rectangle is represented by two points (x1, y1) its bottom left point and (x2, y2) its top right point.
If the rectangles don’t intersect the answer would be simply sum of areas of the individual rectangles. If they intersect then we need to subtract the intersecting area as we account for this area twice in the sum. So the answer is simply area(R1) + area(R2) - intersectingArea(R1, R2).
Let us now look at how to find if the two rectangles are intersecting and the area of their intersection. First let us consider just the case when the rectangles intersect. Here is a diagram showing some possibilities of rectangles intersecting.
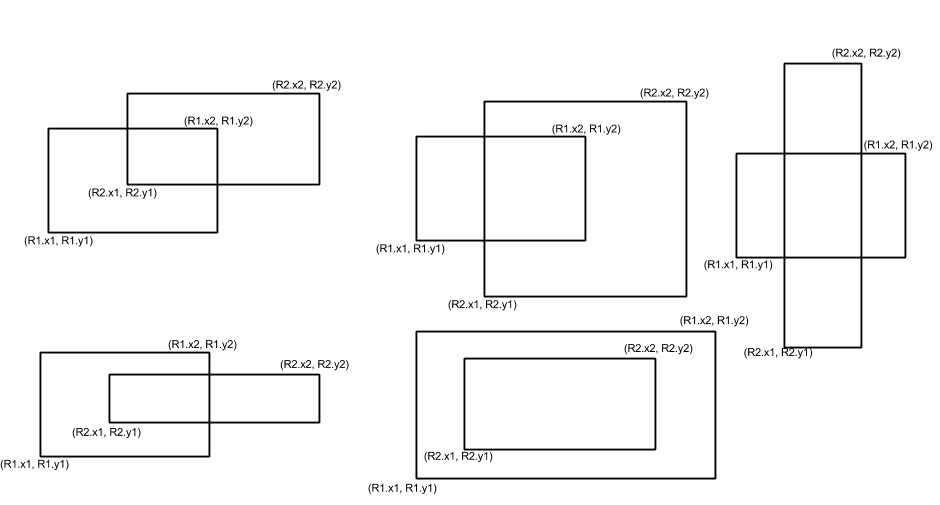
Based on these figures it can be easily observed and also proved for any general case that if the rectangles intersect the lower left point of the rectangle representing the intersecting area is (max(R1.x1, R2.x1), max(R1.y1, R2.y1)) and the top right point is (min(R1.x2, R2.x2), min(R1.y2, R2.y2)). Once we find these points we can find the area of the intersecting region also. Note that the rectangles R1 and R2 are interchangeable it doesn’t matter which one is seen as the first rectangle.
To check if the two rectangles intersect in the first place it is as simple as finding these two points and see it they form a well defined rectangle. If they form a well defined rectangle they intersect otherwise they don’t. Let us call the two points (R3.x1, R3.y1) and (R3.x2, R3.y2), they form a well defined rectangle only if (R3.x1 < R3. x2) and (R3.y1 < R3. y2) as both coordinates of bottom left point have to come before the corresponding coordinates of top right point.
SOLUTIONS
Setter’s Solution: CAKE1AM.cpp
Tester’s Solution: CAKE1AM.cpp
