PROBLEM LINK:
Cassandra is Playing with Polygons
Setter: sayan_kashyapi
Tester: debrc
Editorialist: sayan_kashyapi
DIFFICULTY:
Medium
PREREQUISITES:
Catalan Numbers
PROBLEM:
You are given a polygon with N vertices labelled from 1 to N in clockwise order. You have to return the two values, the number of possible triangulation and the weight of the minimum triangulation. The weight of a triangulation is basically the sum of weights of triangles it consists of, where the weight of a triangle is denoted as the product of the labels of its vertices.
EXPLANATION
The total number of ways of triangulation = C_{(N - 2)}.
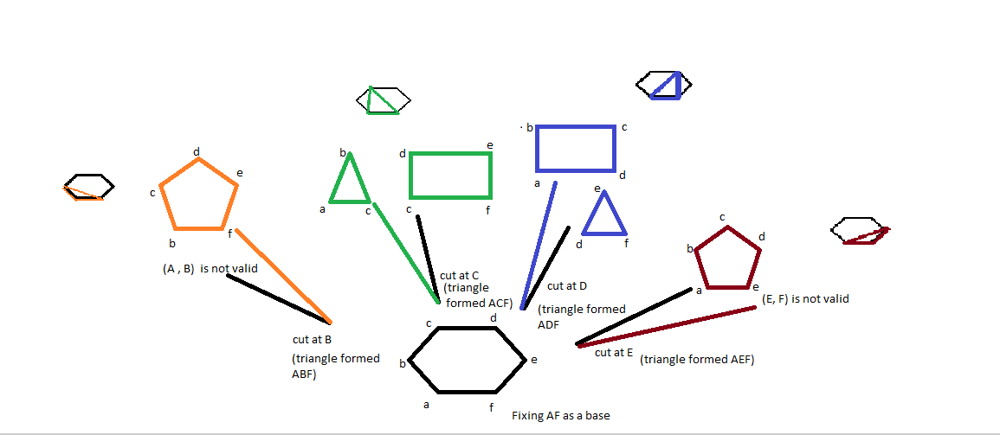
For better understanding of how to find out the minimum weight triangulation follow the image and dry run the code. In the code catalanNumber() function is used to calculate the Nth Catalan Number and minScoreTriangulation() function is used to find out the minimum score triangulation.
TIME COMPLEXITY
Time complexity is O(N^2) for each test case.
SOLUTIONS:
Setter's Solution
C++17
#include <bits/stdc++.h>
#include <boost/multiprecision/cpp_int.hpp>
using boost::multiprecision::cpp_int;
using namespace std;
const int MOD = 1000000007;
void catalanNumber(int n)
{
cpp_int cat_ = 1;
for (cpp_int i = 1; i <= n; i++)
{
cat_ *= (4 * i - 2);
cat_ /= (i + 1);
}
cout << (cat_) % MOD << " ";
}
int minScoreTriangulation(vector<int>& A) {
int n = A.size();
vector<vector<int>>dp(n, vector<int>(n, 0));
for (int L = 3; L <= n; L++)
for (int i = 0; i < n - L + 1; i++) {
int j = i + L - 1;
dp[i][j] = INT_MAX;
for (int k = i + 1; k < j; k++)
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + (A[i] * A[k] * A[j]) );
}
return dp[0][n - 1];
}
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
vector<int> A;
for (int i = 1; i <= n; i++)
A.push_back(i);
catalanNumber(n - 2);
cout << minScoreTriangulation(A) << endl;
}
}
Tester's Solution
PYPY3
import math,sys
MAX=1001
MOD=1000000007
INT_MAX=sys.maxsize
dp=[0 for _ in range(MAX)]
def precompute():
dp[0]=1
for i in range(1,MAX):
dp[i] = 0
for j in range(0,i):
dp[i]=(dp[i]+(dp[j]*dp[i-j-1])%MOD)%MOD
def minScoreTriangulation(A):
n=len(A)
dp=[[0 for _ in range(n)] for _ in range(n)]
for L in range(3,n+1):
for i in range(0,n-L+1):
j=i+L-1
dp[i][j]=INT_MAX
for k in range(i+1,j):
dp[i][j] = min(dp[i][j],(dp[i][k]+dp[k][j]+(A[i]*A[k]*A[j])))
return dp[0][n-1]
precompute()
for _ in range(int(input())):
n=int(input())
a=[i for i in range(1,n+1)]
print(dp[n-2],minScoreTriangulation(a))
Python3.6
import math,sys
MAX=1001
MOD=1000000007
INT_MAX=sys.maxsize
dp=[0 for _ in range(MAX)]
def precompute():
dp[0]=1
for i in range(1,MAX):
dp[i] = 0
for j in range(0,i):
dp[i]=(dp[i]+(dp[j]*dp[i-j-1])%MOD)%MOD
def minScoreTriangulation(A):
n=len(A)
dp=[[0 for _ in range(n)] for _ in range(n)]
for L in range(3,n+1):
for i in range(0,n-L+1):
j=i+L-1
dp[i][j]=INT_MAX
for k in range(i+1,j):
dp[i][j] = min(dp[i][j],(dp[i][k]+dp[k][j]+(A[i]*A[k]*A[j])))
return dp[0][n-1]
precompute()
for _ in range(int(input())):
n=int(input())
a=[i for i in range(1,n+1)]
print(dp[n-2],minScoreTriangulation(a))
Feel free to Share your approach.
Suggestions are welcomed as always had been.