Problem Link:
Author & Editorialis: Arun Das
Tester: Jatin Nagpal
DIFFICULTY:
EASY-MEDIUM
PREREQUISITES:
DFS(Depth First Search)
PROBLEM:
Given a rooted tree and Q queries, in each query transfer the values of nodes at a non-zero even distance to the source node. Print the final values of the nodes.
QUICK EXPLANATION:
Create a N\times2 2D array to keep track of whether nodes at all even/odd distances from a node have been visited. Start a DFS from the source node in each query and if all even/odd nodes have already been visited skip the entire subtree.
EXPLANATION:
Notice that once we complete the DFS of a source node, all values at non-zero even distances in its subtree will become zero and will not change further.
Let’s see how the search goes for each query.
- First, we start looking for nodes at an even distance from the source. (The source value is not added to itself)
- As the DFS continues, we look for odd distanced nodes from the child of the source.
- Next, we look for even distanced nodes from the grandchildren of the source. (These values are added to the source)
We see that all nodes in a subtree can be divided into 2 parts - Nodes that are at an even distance from the root of the subtree and nodes that are at an odd distance. So let’s create an N\times2 size 2 dimensional visited array to keep track of this. visited[i][0] will be zero if all nodes in the subtree of i that are at non-zero even distances from i are 0 and visited[i][1] will keep track of the same for odd distanced nodes.
Now when we are doing the DFS and looking for even distanced nodes from the current node, we check visited[current][0]. If this value is 0, it means that all nodes at even distances haven’t been visited and we continue the DFS. Otherwise, all nodes at an even distance from this node have been visited and we can just add the value of the current node to the source (if it’s not the source itself) and skip the entire subtree.
Why add if visited?
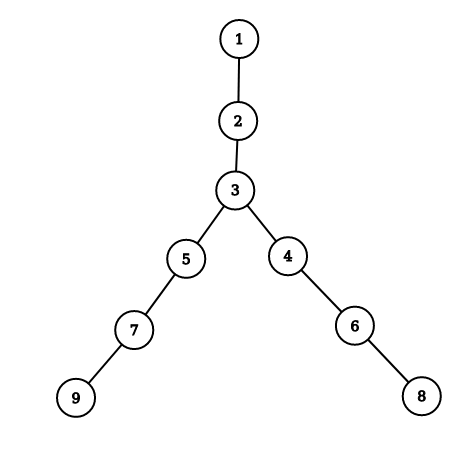
Consider the following tree and the queries → 5, 4, 2 in order.
After the first and second queries, visited[5][0] and visited[4][0] will become 1 but note that the values of the source itself may not become 0. When we query for 2, we need to add the values of nodes 4 and 5.
The time complexity of this solution in O(n).
Why?
Each node will be accessed at most 3 times.
- Once when this node is the query. After the query visited[node][0] will become 1.
- Once when a query starts from an ancestor of this node which is at an even distance. After this query, the value of this node will become 0.
- Once when a query starts from an odd distanced ancestor of this node. After this query visited[node][1] will become 1.
Any further queries will either terminate in one of its ancestors or can be skipped entirely.
Things to watch out for
- Make sure to mark the source node visited or you might TLE in case the input is star-shaped.
- Use the appropriate data type since the answer might be as big as about 1014
This can be implemented in more than one ways and there can be other different approaches. Feel free to discuss them. ![]()
SOLUTIONS:
Setter's Solution(with comments)
#include<bits/stdc++.h>
using namespace std;
#define int long long
int visited[200005][2];
int values[200005], parent[200050];
void dfs(int vertex, int parity, vector<int> tree[], int source, int parent){
//if the vertex is not source and distance from source is even add the value
if(vertex != source && parity == 0){
values[source] += values[vertex];
values[vertex] = 0;
}
//if visited[vertex][1] == 1, all the nodes at odd distance
//from the current vertex are zero. So there is no need to go further.
if(visited[vertex][parity] == 0){
for(auto x: tree[vertex]){
if(x != parent){
//if we are looking for nodes at an even distance from current node,
//then we have to look for nodes at an odd distance from this node's children
dfs(x, parity^1, tree, source, vertex);
}
}
//if parity == 1, all nodes at odd distance from this vertex have been visited
//if parity == 0, all nodes at even distance from this vertex have been visited
visited[vertex][parity] = 1;
}
}
void findParents(int v, vector<int> tree[], int par){
parent[v] = par;
for(auto x: tree[v])
if(x != par)
findParents(x, tree, v);
}
int32_t main(){
// ios_base::sync_with_stdio(false);
// cin.tie(NULL);
int t;
cin >> t;
while(t--){
int n, i, j, x, u, v, q;
cin >> n >> q;
for(i=0; i<200005; i++){
visited[i][0] = 0;
visited[i][1] = 0;
}
// take the input values
for(i=0; i<n; i++)
cin >> values[i];
//take the input tree
vector<int> tree[n];
for(i=0; i<n-1; i++){
cin >> u >> v;
u--; v--;
tree[u].push_back(v);
tree[v].push_back(u);
}
// find the parent of each vertex
findParents(0, tree, -1);
while(q--){
cin >> x; x--;
if(visited[x][0] == 1){
continue;
}
dfs(x, 0, tree, x, parent[x]);
visited[x][0] = 1;
}
for(i=0; i<n; i++){
cout << values[i] << " ";
}
cout << "\n";
}
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
#define ff first
#define ss second
#define MP make_pair
#define PB push_back
#define ll long long
#define int long long
#define f(i,x,n) for(int i=x;i<n;i++)
#define ld long double
const int mod=1000000007;
const int INF=1e18;
int n,q,a[200005],vis[200005],ans[200005];
vector <int> gp[200005];
pair <int,int> dfs(int i,int par,int state) {
int flag=0;
if(vis[i]==1 && (state&1) ==0)
{
state|=1;
flag=1;
}
pair <int,int> ret={0,0};
for(auto j: gp[i]) {
if(j!=par) {
pair <int,int> tmp=dfs(j,i, (state%2)*2 + state/2 );
ret.ff+=tmp.ff;
ret.ss+=tmp.ss;
}
}
ret.ff+=a[i];
if(flag==1)
ans[i]=ret.ff;
else
ans[i]=(1^(state&1))*a[i];
ret.ff=ret.ff^ret.ss;
ret.ss=ret.ff^ret.ss;
ret.ff=ret.ff^ret.ss;
return ret;
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin>>t;
while(t--) {
cin>>n>>q;
f(i,1,n+1)
{
vis[i]=0;
gp[i].clear();
ans[i]=0;
cin>>a[i];
}
f(i,0,n-1) {
int u,v;
cin>>u>>v;
gp[u].push_back(v);
gp[v].push_back(u);
}
while(q--) {
int Q;
cin>>Q;
vis[Q]=1;
}
dfs(1,0,0);
f(i,1,n+1)
cout<<ans[i]<<" ";
cout<<'\n';
}
return 0;
}