CFROD - Editorial

editorial
, , ,
1

PROBLEM LINK:

Practice
Contest

Author: Vikas Yadav
Tester: Lalit Singh
Editorialist: Vikas Yadav

DIFFICULTY:

EASY

PREREQUISITES:

LCM

PROBLEM:

A rod in cut into N equal parts. The resulting portions are then cut into A1, A2, ... An equal parts respectively. If each of the resulting portions have integral lengths, then find minimum length of the rod.

QUICK EXPLANATION:

Find the LCM of A1, A2, ... An and store in variable result_lcm.
Print N * result_lcm as final output.

EXPLANATION:

LCM of A1, A2, ... An will give common length for each parts so that after final cut will of integral length (1). Now when we multiply by N then we get minimum total length of rod.
e.g. if a rod has to cut in 2 equal parts then each parts has to cut into 1 and 2 parts respectively.
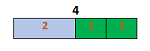
CFROD
Minimum length of rod = LCM(1, 2) * 2 = 4.

Common Mistake:

Use proper datatype to store final output.

SOLUTIONS:

Tester's Solution 
# Chef and Rod

def find_lcm(num1, num2):
 
    if(num1 > num2): 
        num = num1 
        den = num2 
    else: 
        num = num2 
        den = num1 
    rem = num % den 
    while(rem != 0): 
        num = den 
        den = rem 
        rem = num % den

    gcd = den 
    lcm = int(int(num1 * num2)/int(gcd)) 
    
    return lcm 

for _ in range(int(input())):

	n = int(input())
	a = list(map(int, input().split()))

	num1 = a[0]
	num2 = a[1]
	lcm = find_lcm(num1, num2)

	for i in range(2, len(a)):
		lcm = find_lcm(lcm, a[i])

	print(lcm * n)