PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Srikkanth R and Daanish Mahajan
Tester: Istvan Nagy
Editorialist: Taranpreet Singh
DIFFICULTY
Easy-Medium
PREREQUISITES
Greedy, Priority Queue
PROBLEM
There are N people traveling on a train, which has only one charging point. For each person, A_i denotes the amount of charging time i-th person requires, and T_i denotes the time at which i-th person gets off the train.
Determine a schedule of using the charging point containing at most 2*N intervals such that no two intervals intersect and the number of people having their charging requirements fulfilled is maximized.
QUICK EXPLANATION
- Consider people in decreasing order of their exit time, and maintain information of people already added, and their charge requirements left.
- If the current person leaves at time t, then try to assign all time after t to people on the train after time t.
- When choosing whom to assign time, it is optimal to assign a charging point to the person among available people, who have minimum charging requirements.
EXPLANATION
Let’s consider an example first. Let’s assume N = 3 and WLOG assume T_1 \lt T_2 \lt T_3 denoting the exit times of people, and A_1, A_2 and A_3 denoting their charging requirements.
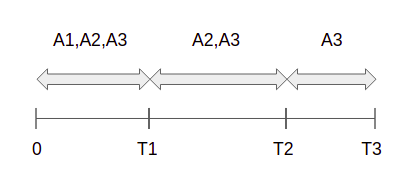
- In time interval [0, T_1), any of the three people can use charging point.
- In time interval [T_1, T_2), person 2 and 3 can use charging point.
- In time interval [T_2, T_3), only person 3 can use charging point.
Since for interval [T_2, T_3), only person 3 can use charging point, so let’s devote time interval [T_2, T_3) to person 3, reducing A_3 by min(A_3, T_3-T_2).
Now, since person 2 and person 3 are the only ones who can use charging point in time [T_1, T_2). Their charging requirements are A_2 and max(0, A_3 - (T_3-T_2)).
It is important to see that both person 2 and person 3 now have the same time interval [0, T_2) to fulfill their requirements. So we can easily switch time devoted to person 2 to person 3 or vice versa, without violating any constraints. This is the reason we are able to apply the greedy strategy stated below.
Our goal is to maximize the number of people having fulfilled charging requirements, so it makes sense to satisfy the people with minimum remaining charging requirements first.
Hence, first devote time from interval [T_1, T_2) to the person, who needs charging point for lesser time. Hence, if A_2 \lt max(0, A_3-(T_3-T_2)), devote it to person 2 otherwise to person 3.
Solution
We saw that by processing the time intervals in reverse order, we were able to greedily choose the time intervals to denote to people.
We can generalize the above fact as follows.
Consider people in decreasing order of their exit time, we can see that once a person is available, that person remains available till time reaches 0. So, to maximize the number of people having their requirements fulfilled, we must pick the person having the lowest requirement at each step. We can choose greedily from people who can use charging points at the current moment, the one with the minimum remaining requirement.
This process can be considered similar to the well-known scheduling method called Shortest Remaining Time
This forms the core of the solution.
Implementation
Let’s maintain a structure storing pairs (id, x) denoting that person numbered id requires x units of time on charging point, which is initially empty. Let’s assume current time ct = \infin
Considering people in decreasing order of time, let’s say we are considering person p, So now we can assign charging point for time interval [T_p, ct) to people already in structure.
Let’s pick from structure, the pair with smallest x, and devote it y = min(x, ct-T_p) charging time. ct also gets reduced by y and pair (id, x) is replaced by (id, x-y), as time interval [ct-y, ct) is denoted to person numbered id. Discard the pair if x-y = 0. We shall repeat this procedure while we have ct \gt T_p and structure is non-empty.
This way, we have either utilized the whole time interval [T_p, ct), or all people leaving after T_p are satisfied. So we set ct = T_p now, and add tuple (p, A_p) into the structure.
The structure needs to support the addition of a pair and popping out pair with minimum x, so a heap is a suitable data structure for this problem.
Number of intervals
We can prove that the number of time intervals is bounded by 2*N. An interval breaks when the charging requirements of some person are fulfilled (which may happen at most N times) or ct - T_p \lt x when considering pair (id,x) and the next person leaves the train at T_p. This situation may happen at most N times as well, as each person may break at most 1 interval.
So the number of intervals found this way do not exceed 2*N.
Related problem
An almost similar problem: IPCTRAIN
TIME COMPLEXITY
The time complexity is O(N*log(N)) per test case.
SOLUTIONS
Setter's Solution
#include <bits/stdc++.h>
#define LL long long
using namespace std;
auto random_seed = chrono::steady_clock::now().time_since_epoch().count();
mt19937 rng(random_seed);
clock_t start = clock();
LL readInt(LL l, LL r, char endd) {
LL x = 0;
char ch = getchar();
bool first = true, neg = false;
while (true) {
if (ch == endd) {
break;
} else if (ch == '-') {
assert(first);
neg = true;
} else if (ch >= '0' && ch <= '9') {
x = (x << 1) + (x << 3) + ch - '0';
} else {
assert(false);
}
first = false;
ch = getchar();
}
if (neg) x = -x;
if (x < l || x > r) {
cerr << l << " " << r << " " << x << " failed\n";
}
assert(l <= x && x <= r);
return x;
}
string readString(int l, int r, char endd) {
string ret = "";
int cnt = 0;
while (true) {
char g = getchar();
assert (g != -1);
if (g == endd) {
break;
}
++cnt;
ret += g;
}
assert(l <= cnt && cnt <= r);
return ret;
}
LL readIntSp(LL l, LL r) {
return readInt(l, r, ' ');
}
LL readIntLn(LL l, LL r) {
return readInt(l, r, '\n');
}
string readStringSp(int l, int r) {
return readString(l, r, ' ');
}
string readStringLn(int l, int r) {
return readString(l, r, '\n');
}
const int M = (int)3e5;
const int C = (int)3e5;
int sum_n = 0;
array<int, 3> v[M];
void solve() {
int n = readIntLn(1, M);
sum_n += n;
for (int i=0;i<n;++i) {
v[i][1] = readInt(0, C, " \n"[i==n-1]);
v[i][2] = i;
}
for (int i=0;i<n;++i) v[i][0] = readInt(0, C, " \n"[i==n-1]);
sort(v, v+n);
// for (int i=0;i<n;++i) cerr << v[i][0] << " " << v[i][1] << '\n';
set<pair<int, int>> st;
LL have = 0;
for (int i=0;i<n;++i) {
st.insert({v[i][1], i});
// cerr << v[i][1] << " " << "added\n";
if (have + v[i][1] <= v[i][0]) {
have += v[i][1];
} else {
auto it = st.end();
it--;
have += v[i][1] - it->first;
// cerr << it->first << " " << "removed\n";
st.erase(it);
}
}
vector<pair<int, int>> ret;
LL go = 0;
for (auto &p : st) {
int ind = p.second;
// cerr << go + v[ind][1] << " " << v[ind][0] << " wtf\n";
// if (go + v[ind][1] <= v[ind][0]) {
ret.push_back({v[ind][0], ind});
// go += v[ind][1];
// }
}
sort(ret.begin(), ret.end());
int pre = 0;
vector<array<int, 3>> vout;
for (int i=0;i<(int)ret.size();++i) {
int ind = ret[i].second;
// cout << v[ind][2] + 1 << " " << pre << " " << pre + v[ind][1] << '\n';
vout.push_back({v[ind][2]+1, pre, pre+v[ind][1]});
assert(pre + v[ind][1] <= v[ind][0]);
pre += v[ind][1];
}
cout << vout.size() << '\n';
shuffle(vout.begin(), vout.end(), rng);
for (auto it : vout) cout << it[0] << " " << it[1] << " " << it[2] << '\n';
}
int main() {
// Start solution here use readIntLn, readIntSp and readStringSp and readStringLn
// for reading input
int T = readIntLn(1, M);
while (T--) {
solve();
}
assert(1 <= sum_n && sum_n <= M);
// End solution here
assert(getchar() == EOF);
cerr << fixed << setprecision(10);
cerr << "Time taken = " << (clock() - start) / ((double)CLOCKS_PER_SEC) << " s\n";
return 0;
}
Tester's Solution
#include <iostream>
#include <cassert>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <random>
#ifdef HOME
#include <windows.h>
#endif
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
template<class T> bool umin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool umax(T &a, T b) { return a < b ? (a = b, true) : false; }
using namespace std;
int main(int argc, char** argv)
{
#ifdef HOME
if(IsDebuggerPresent())
{
freopen("../in.txt", "rb", stdin);
freopen("../out.txt", "wb", stdout);
}
#endif
ios::sync_with_stdio(false);
int T;
cin >> T;
forn(tc, T)
{
uint32_t n;
cin >> n;
vector<tuple<uint32_t, uint32_t, uint32_t>> A(n);//T, A, id
vector< tuple<uint32_t, uint32_t, uint32_t>> ch;//index, from, to
multimap<uint32_t, uint32_t> remMap;//rem, id
vector<uint32_t> remV(n);
forn(i, n)
get<2>(A[i]) = i;
for (auto& ai : A)
{
cin >> get<1>(ai);
remV[get<2>(ai)] = get<1>(ai);
}
for (auto& ai : A)
cin >> get<0>(ai);
sort(A.begin(), A.end());
reverse(A.begin(), A.end());
uint32_t currTime = 1'000'000'001;
forn(i, n)
{
const auto& nextV = A[i];
uint32_t nextT = get<0>(nextV);
uint32_t remT = currTime - nextT;
while (remT && remMap.size())
{
uint32_t remTime = remMap.begin()->first;
uint32_t remId = remMap.begin()->second;
remMap.erase(remMap.begin());
if (remTime <= remT)
{
ch.push_back({ remId, currTime - remTime, currTime });
currTime -= remTime;
remT -= remTime;
remV[remId] -= remTime;
}
else
{
ch.push_back({remId, nextT, currTime});
remTime -= remT;
remMap.insert({ remTime, remId });
remV[remId] -= remT;
remT = 0;
}
}
currTime = nextT;
remMap.insert({ get<1>(nextV), get<2>(nextV) });
}
while (currTime && remMap.size())
{
uint32_t remTime = remMap.begin()->first;
uint32_t remId = remMap.begin()->second;
remMap.erase(remMap.begin());
if (remTime <= currTime)
{
ch.push_back({ remId, currTime - remTime, currTime });
currTime -= remTime;
remV[remId] -= remTime;
}
else
break;
}
reverse(ch.begin(), ch.end());
ch.erase(remove_if(ch.begin(), ch.end(), [&](auto chi) {return remV[get<0>(chi)]; }), ch.end());
vector< tuple<uint32_t, uint32_t, uint32_t>> ch2;
for (const auto& chi : ch)
{
if (!ch2.empty() && get<0>(chi) == get<0>(ch2.back()))
{
assert(get<2>(ch2.back()) == get<1>(chi));
get<2>(ch2.back()) = get<2>(chi);
}
else
ch2.push_back(chi);
}
ch.swap(ch2);
printf("%u\n", static_cast<uint32_t>(ch.size()));
for (auto chi : ch)
{
printf("%u %u %u\n", get<0>(chi) + 1, get<1>(chi), get<2>(chi));
}
}
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class CHARGE{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni();
Person[] P = new Person[N];
for(int i = 0; i< N; i++)P[i] = new Person(1+i, ni(), -1);
for(int i = 0; i< N; i++)P[i].exit = ni();
Arrays.sort(P, (Person p1, Person p2) -> Integer.compare(p2.exit, p1.exit));
PriorityQueue<Person> q = new PriorityQueue<>((Person p1, Person p2) -> Integer.compare(p1.charge, p2.charge));
int time = (int)1e9;
int cnt = 0;
for(int i = 0; i< N; i++){
while(!q.isEmpty() && time > P[i].exit){
Person p = q.poll();
int ch = Math.min(time-P[i].exit, p.charge);
p.charge -= ch;
time -= ch;
p.list.add(new int[]{time, time+ch});
cnt++;
if(p.charge > 0)q.add(p);
}
time = P[i].exit;
q.add(P[i]);
}
while(!q.isEmpty() && time > 0){
Person p = q.poll();
int ch = Math.min(time, p.charge);
p.charge -= ch;
time -= ch;
p.list.add(new int[]{time, time+ch});
cnt++;
if(p.charge > 0)q.add(p);
}
pn(cnt);
for(Person p:P)for(int[] op:p.list)pn(p.ind+" "+op[0]+" "+op[1]);
}
class Person{
int ind, charge, exit;
ArrayList<int[]> list;
public Person(int i, int c, int e){
ind = i;
charge = c;
exit = e;
list = new ArrayList<>();
}
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new CHARGE().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()