PROBLEM LINK:
Author: Roman Furko
Testers: Pushkar Mishra and Sergey Kulik
Editorialist: Pawel Kacprzak
Russian Translator: Sergey Kulik
Mandarian Translator: Gedi Zheng
DIFFICULTY:
Easy
PREREQUISITES:
bits, implementation
PROBLEM:
You are given a square matrix A of size N. For a submatrix B of A, we define its value as the bitwise XOR of all elements of B. Your task is to find the maximum value among all submatrices of A.
QUICK EXPLANATION:
Since N \leq 70, if we are able to compute a value for a given submatrix in constant time, we can iterate over all submatrices and return the maximum value. In order to compute the value for a given submatrix fast, we first compute values of all submatrices which have the upper-left corner at (1, 1). Then we can use these values to compute every other value using properties of XOR operation.
EXPLANATION:
Let C[i][j] be the value of the submatrix which has its upper left corner at (1, 1) and its bottom right corner in (i, j). We can compute the C table in O(N^4) or O(N^3), or even O(N^2), but since N is quite small, it does not matter which method you choose.
After that, we notice the major property of XOR, i.e. x \oplus x = 0. Using this property and precomputed table C, we can easily compute the value for any submatrix R in constant time. Let’s consider the below illustration and define 5 submatrices:
- R, the Red submatrix, we are interested in computing its value
- B, the Blue submatrix, we have its value computed and stored in C table
- G, the Green submatrix, we have its value computed and stored in C table
- Y, the Yellow submatrix, we have its value computed and stored in C table
- P, the Purple submatrix, we have its value computed and stored in C table
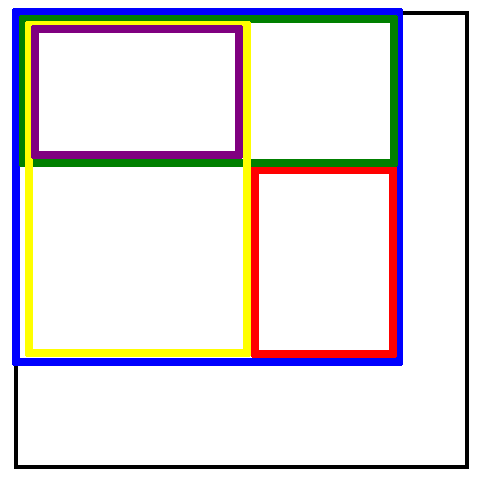
Let’s define, for the above matrices, C_X to be the value from C table for a submatrix X, for example C_R is the value of the matrix R. Then C_R = C_B \oplus C_G \oplus C_Y \oplus C_P
This is duo to the major property of XOR and the fact that both C_G and C_Y contain C_P as a submatrix.
Time complexity
For a single test case it is O(N^4) because we can compute the C table in O(N^4); and we compute the value for every submatrix in a constant time, and there are O(N^4) different submatrices.


