PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author: Rahul Dugar
Tester: Suchan Park
Editorialist: William Lin
DIFFICULTY:
Medium
PREREQUISITES:
Graphs, Bipartite Matching
PROBLEM:
Given K permutations of 1 to N, construct a graph with the following properties: 1. Each permutation is a valid topological sort 2. The outdegree of each node is at most 1 3. The number of nodes with indegree 0 is as small as possible.
QUICK EXPLANATION:
The answer will only consist of paths. If we consider the graph with all edges which are allowed by condition 1, we are trying to cover all nodes with the minimum number of paths (with edges from the graph), which can be solved with bipartite matching.
EXPLANATION:
Observation 1. We can model the answer as a forest.
Explanation
Each node has an outdegree of at most 1. If the node has an outdegree of 0, then we will make it the root of a tree. Otherwise, the parent of the node is the node that it points to. Note that the answer is acyclic so we won’t have the case where cycles are formed.
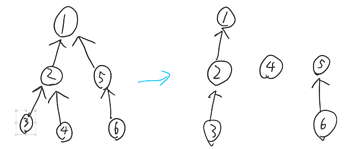
Observation 2. An optimal answer consists of a set of paths.
Proof
We want to minimize the number of nodes with an indegree of 0, which are the leaf nodes. But note that if we have a tree, we can split it into a set of paths as shown, while still having the same number of leaves:
As we only remove edges to convert the tree into a set of paths, conditions 1 (valid topological sort) and 2 (outdegree of at most 1) will still be satisfied.
Each path has exactly one node with 0 indegree, so we want to minimize the number of paths.
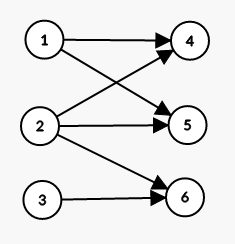
Let G contain the set of edges which don’t satisfy condition 1 (all edges except A_{k, j} to A_{k, i} for some k and i<j).
Observation 3. G is acyclic.
Proof
If we only have one permutation A_1, G contains all edges A_{1, i} to A_{1, j} such that i<j, which is acyclic. Adding more permutations only removes edges from G, so G will still be acyclic.
The problem reduces to finding the minimum number of paths to cover G, which is acyclic. This is a well-known problem (Solving Minimum Path Cover on a DAG | by Rıza Özçelik | Towards Data Science) which can be solved with maximum bipartite matching. The final complexity is O(N^3).
SOLUTIONS:
Setter's Solution
#pragma GCC optimze("Ofast")
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
#ifndef rd
#define trace(...)
#endif
#define endl '\n'
#define pb push_back
#define fi first
#define se second
#define int long long
typedef long long ll;
typedef long double f80;
#define double long double
#define pii pair<int,int>
#define pll pair<ll,ll>
#define sz(x) ((long long)x.size())
#define fr(a,b,c) for(int a=b; a<=c; a++)
#define rep(a,b,c) for(int a=b; a<c; a++)
#define trav(a,x) for(auto &a:x)
#define all(con) con.begin(),con.end()
const ll infl=0x3f3f3f3f3f3f3f3fLL;
const int infi=0x3f3f3f3f;
// const int mod=998244353;
int mod=1000000007;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef tree<pii, null_type, less<pii>, rb_tree_tag, tree_order_statistics_node_update> oset;
auto clk=clock();
mt19937_64 rang(10);
//mt19937_64 rang(chrono::high_resolution_clock::now().time_since_epoch().count());
int rng(int lim) {
uniform_int_distribution<int> uid(0,lim-1);
return uid(rang);
}
int powm(int a, int b) {
int res=1;
while(b) {
if(b&1)
res=(res*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return res;
}
struct BipartiteMatcher{
vector<vector<int>> G;
vector<int> L, R, Viz;
void init(int n, int m){
G.clear(), L.clear(), R.clear(), Viz.clear();
G.resize(n), L.resize(n, -1), R.resize(m, -1), Viz.resize(n, 0);
}
void AddEdge(int a, int b){ G[a].push_back(b); }
bool Match(int node){
if(Viz[node]) return 0;
Viz[node] = 1;
for(auto vec : G[node]){
if(R[vec] == -1 || Match(R[vec])) {
L[node] = vec;
R[vec] = node;
return 1;
}
}
return 0;
}
int Solve(){
bool ok = 1;
while(ok){
ok = 0;
fill(Viz.begin(), Viz.end(), 0);
fr(i, 0, L.size() - 1)
if(L[i] == -1)
ok |= Match(i);
}
int ret = 0;
fr(i, 0, L.size() - 1)
ret += (L[i] != -1);
return ret;
}
} bm;
bool adj[505][505];
int a[505];
void solve() {
int n,k;
cin>>n>>k;
//at-first any ordering is possible.
fr(i,1,n)
fr(j,1,n)
adj[i][j]=1;
fr(i,1,k) {
fr(j,1,n)
cin>>a[j];
//removing those edges which cannot be added.
fr(j,1,n)
fr(l,j,n)
adj[a[l]][a[j]]=0;
}
bm.init(n+1, n+1);
fr(i,1,n)
fr(j,1,n)
if(adj[i][j])
bm.AddEdge(i,j); //adding edges to the bipartite matcher.
cout<<n-bm.Solve()<<endl;
fr(i,1,n) {
if(~bm.L[i])
cout<<bm.L[i]<<" \n"[i==n];
else
cout<<0<<" \n"[i==n];
}
}
signed main() {
ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0);
srand(chrono::high_resolution_clock::now().time_since_epoch().count());
cout<<fixed<<setprecision(8);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
const int BUFFER_SIZE = int(1.1e5);
char _buf[BUFFER_SIZE + 10];
int _buf_pos, _buf_len;
char seekChar() {
if(_buf_pos >= _buf_len) {
_buf_len = fread(_buf, 1, BUFFER_SIZE, stdin);
_buf_pos = 0;
}
assert(_buf_pos < _buf_len);
return _buf[_buf_pos];
}
bool seekEof() {
if(_buf_pos >= _buf_len) {
_buf_len = fread(_buf, 1, BUFFER_SIZE, stdin);
_buf_pos = 0;
}
return _buf_pos >= _buf_len;
}
char readChar() {
char ret = seekChar();
_buf_pos++;
return ret;
}
int readInt(int lb, int rb) {
char c = readChar();
int mul = 1;
if(c == '-') {
c = readChar();
mul = -1;
}
assert(isdigit(c));
long long ret = c - '0';
int len = 0;
while(!seekEof() && isdigit(seekChar()) && ++len <= 19) {
ret = ret * 10 + readChar() - '0';
}
ret *= mul;
assert(len <= 18);
assert(lb <= ret && ret <= rb);
return (int)ret;
}
void readEoln() {
char c = readChar();
//assert(c == '\n');
assert(c == '\n' || (c == '\r' && readChar() == '\n'));
}
void readSpace() {
assert(readChar() == ' ');
}
namespace BipartiteMatching {
const int MAXN = 505, MAXM = 50005;
std::vector<int> gph[MAXN];
int dis[MAXN], l[MAXN], r[MAXM], vis[MAXN];
void clear(){ for(int i=0; i<MAXN; i++) gph[i].clear(); }
void add_edge(int l, int r){ gph[l].push_back(r); }
bool bfs(int n){
std::queue<int> que;
bool ok = 0;
memset(dis, 0, sizeof(dis));
for(int i=0; i<n; i++){
if(l[i] == -1 && !dis[i]){
que.push(i);
dis[i] = 1;
}
}
while(!que.empty()){
int x = que.front();
que.pop();
for(auto &i : gph[x]){
if(r[i] == -1) ok = 1;
else if(!dis[r[i]]){
dis[r[i]] = dis[x] + 1;
que.push(r[i]);
}
}
}
return ok;
}
bool dfs(int x){
if(vis[x]) return false;
vis[x] = 1;
for(auto &i : gph[x]){
if(r[i] == -1 || (!vis[r[i]] && dis[r[i]] == dis[x] + 1 && dfs(r[i]))){
l[x] = i; r[i] = x;
return true;
}
}
return false;
}
int match(int n){
memset(l, -1, sizeof(l));
memset(r, -1, sizeof(r));
int ret = 0;
while(bfs(n)){
memset(vis, 0, sizeof(vis));
for(int i=0; i<n; i++) if(l[i] == -1 && dfs(i)) ret++;
}
return ret;
}
}
int sumN = 0;
void run() {
int N = readInt(1, 500);
sumN += N;
assert(sumN <= 2000);
readSpace();
int K = readInt(1, 100);
readEoln();
std::vector<std::vector<int>> rev;
rev.reserve(K);
for(int k = 0; k < K; k++) {
std::vector<int> pos(N, -1);
for(int i = 0; i < N; i++) {
int j = readInt(1, N) - 1;
if(i+1 < N) readSpace(); else readEoln();
assert(pos[j] == -1);
pos[j] = i;
}
rev.push_back(pos);
}
BipartiteMatching::clear();
std::vector<std::vector<bool>> gph(N, std::vector<bool>(N));
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
bool good = true;
for(int k = 0; k < K && good; k++) good &= rev[k][i] < rev[k][j];
if(good) BipartiteMatching::add_edge(i, j);
}
}
int ans = N - BipartiteMatching::match(N);
printf("%d\n", ans);
for(int i = 0; i < N; i++) {
printf("%d%c", BipartiteMatching::l[i] + 1, i+1 < N ? ' ' : '\n');
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
#endif
int T = readInt(1, 100);
readEoln();
while(T--) {
run();
}
return 0;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
const int mxN=500;
int n, k, a[mxN], p[mxN], mt[mxN];
bool adj[mxN][mxN], vis[mxN];
bool dfs(int u) {
vis[u]=1;
for(int v=0; v<n; ++v) {
if(adj[u][v]&&(mt[v]<0||!vis[mt[v]]&&dfs(mt[v]))) {
mt[v]=u;
return 1;
}
}
return 0;
}
void solve() {
//input
cin >> n >> k;
//all edges are in G initially, except for i->i
memset(adj, 1, sizeof(adj));
for(int i=0; i<n; ++i)
adj[i][i]=0;
//go through permutations
while(k--) {
for(int i=0; i<n; ++i) {
cin >> a[i], --a[i];
//remove edges
for(int j=0; j<i; ++j)
adj[a[j]][a[i]]=0;
}
}
//the rest is standard "min path cover on DAG"
//max matching
memset(mt, -1, 4*n);
int flow=0;
for(int i=0; i<n; ++i) {
memset(vis, 0, n);
flow+=dfs(i);
}
//answer
cout << n-flow << "\n";
for(int i=0; i<n; ++i)
cout << mt[i]+1 << " \n"[i==n-1];
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()