PROBLEM LINK:
Practice
Contest
Video Editorial
Setter: Ritesh Gupta
Tester: Rahul Dugar
Editorialist: Ishmeet Singh Saggu
DIFFICULTY:
Medium
PREREQUISITES:
Ad-hoc, Sets, Searching and Maths
PROBLEM:
A sequence is good if the sequence has a length 2*L and it is possible to perform some number of left rotations (possibly zero) and divide the resulting sequence into two halves (containing the first L and last L elements respectively) such that the smallest value in one half is greater then the largest value in the other half. You are given a sequence of N integers. Find the number of its non-empty contiguous subsequences with even length which is good. Also elements of the sequence A are pair-wise distinct.
QUICK EXPLANATION:
- A good sequence can be represented as one of the following ways, here ’ # 'represents the largest L elements of the good sequence and ’ * ’ represents the smallest L elements.
Configuration 1.*********########
Configuration 2.########*********
Configuration 3.*****#########***
Configuration 4.#####*********### - As in good sequence of length L there are 2 halves. smallerHalf containing smallest L elements and LargerHalf containing largest L element. Try to count the number of ways where the smallest element of the LargerHalf is equal to X, where X is an element of the sequence A.
- Count the ways, where the smallest element of the LargerHalf is equal to X, where X is an element of the sequence A in increasing order of X.
- For each element X you can count the number of ways by maintaining 2 sets for ranges, One set will include non-overlapping ranges of the index with elements < X and the other set will include non-overlapping ranges of the index with elements \geq X, and As we iterate over X we will modify these sets by transferring X from bigElement set to smallElement set(after calculating ways for X) and considering various cases(5 to be exact) of making segments which contain X in LargerHalf and have configuration similar to one of the 4 defined above.
EXPLANATION:
Let’s try to rephrase, what a good sequence means :
- It’s length should be even i.e. 2*L.
- It is possible to form a sequence by applying Left Rotations such that smallest L elements are in one half and largest L elements are in the other half.
I will represent the smallest L elements as ’ * ’ and the largest L elements as ’ # '. So there are 4 possible configurations of a sequence that satisfy the condition of good sequence.
Configuration 1. *********########
Configuration 2. ########*********
Configuration 3. *****#########***
Configuration 4. #####*********###
Now let us propose a proper way to count it.
- As it is of length 2*L, so it has two halves, SmallerHalf = containing smallest L elements and LargerHalf = containing Largest L elements. Let us focus on LargerHalf
- What if we try to fix the smallest element of the LargerHalf, let it be X. Then I have to focus on counting the number of a contiguous subsequence of the sequence A which has the configuration similar to one of the 4 possible configuration define above and containing X as the smallest element in its LargerHalf, where X is an element of the sequence A. Also, note that the elements of the sequence A are distinct, So it will help us to prevent overcounting.
- So let’s try to visualize how these configurations will look in the sequence A. I will represent elements \geq X by ’ # ’ and elements < X by ’ * '. NOTE, when we represent the elements of A as defined we will get the structure similar to an alternate sequence of segments of #'s and *'s. Example -
######***############*****##********#####...-
Case 1, following Configuration 1, the ‘#’ in red color is X and it is in segment 5. We have to count all possible for all L considering segment 4 and 5 for which X is included, which poses a restriction that minimum length of L should be 3 as X is the third element and we have to include it. And the maximum L should be min(LengthOfSegment4, LengthOfSegment5).

-
Case 2, following Configuration 2, the minimum length of L should 4 as X is at 4th from the last. This case considers segment 5 and 6. And the maximum L should be min(LengthOfSegment5, LengthOfSegment6).

-
Case 3, following Configuration 3, this case considers segments 3, 4 and 5. Note here L should be exactly equal to the length of segment 4 as it is completely taken and length of segment 4 should be at least (1 + position of X in the segment from left), to make this case possible as it requires to take at least 3 elements(in this example) from the left of the segment 5 and at least one element from the right of segment 3. So after subtracting (1 + position of X in the segment from left) from L let it become L'. Now you have to take some elements(possibly zero) from segment 3 and some elements(possibly zero) from segment 5 such that there sum is equal to L', all those ways will be added to our answer. Similarly, we do the counting for the Case 4 and Case 5 below.
For exact way to count it you can refer to editorialist's code(I have commented it to make it easy to understand)

-
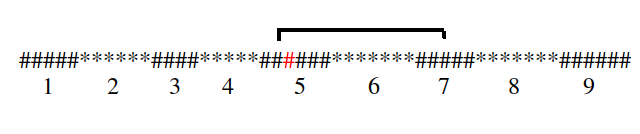
Case 4, following Configuration 3, this case considers segments 5, 6 and 7. L should be exactly equal to the length of segment 6 as it is completely taken and length of segment 6 should be at least (1 + position of X in the segment from right), to make this case possible as it requires to take at least 4 elements(in this example) from the right of the segment 5 and at least one element from the left of segment 7.
-
Case 5, following Configuration 4, this case consider segments 4, 5 and 6. L should be exactly equal to the length of segment 5 as it is completely taken and length of segment 5 should be at least 2, to make this case possible as it requires to take at least 1 element from the right of the segment 4 and at least one element from the left of segment 6.
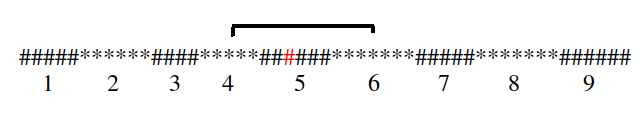
-
You will note something after going through all the cases that, If X is present in segment number Y then you only need segments Y-2, Y-1, Y, Y+1 and Y+2 and position of X in segment Y to compute all the good sequence containing X as the smallest element of the LargerHalf, so if we efficiently compute this we can do this process for all possible X and will get our final answer.
Now let’s go into implementation details.
- Let us iterate through X in increasing order as it will help us maintain elements < current X and elements \geq to current X efficiently.
- Maintain 2 sets for ranges, One set will include non-overlapping ranges of the index(think why?) with elements < X and the other set will include non-overlapping ranges of the index with elements \geq X, and As we iterate over X we will modify these sets by transferring X from bigElement set to smallElement set(after calculating ways for X). NOTE segments are stored as pairs in the set, where the first element is the right border and the second element is the left. Initially smallElement is empty and bigElement has one range equal to [1, N]
- Modification of bigElement set.
// here idx is the index of X.
pair<int, int> seg = *bigElement.lower_bound(make_pair(idx, -1)); // finding the segment which contains X.
bigElement.erase(seg); // deleting the current segment as it will be modified.
int L = seg.second, R = seg.first;
if(L < idx) bigElement.insert(make_pair(idx-1, L)); // if there is some big elements to the left of X.
if(R > idx) bigElement.insert(make_pair(R, idx+1)); // if there is some big elements to the right of X.
- Modification of smallElement set.
// here idx is the index of the X.
int L = idx, R = idx; // current segment to add (idx, idx)
// below I am checking if any range of type (l, idx-1) exist, and if it then
// I will merge it with (idx, idx).
pair<int, int> seg = *smallElement.lower_bound(make_pair(idx-1, -1));
if((seg.first == idx-1) && (seg.first != 0) && (seg.first != N+1)) {
smallElement.erase(seg);
L = seg.second;
}
// below I am checking if any range of type (idx+1, r) exist, and if it then
// I will merge it.
seg = *smallElement.lower_bound(make_pair(idx+1, -1));
if((seg.second == idx+1) && (seg.second != 0) && (seg.second != N+1)) {
smallElement.erase(seg);
R = seg.first;
}
smallElement.insert({R, L}); // adding to the set.
-
Now how to compute segment Y-2, Y-1, Y, Y+1 and Y+2. You can find the segment Y by applying lower bound(it is similar to intersection check trick) on the set bigElement for pair {index(X), -1}.
- You can find segment Y-1 by applying lower bound on the set smallElement for pair {leftBorderOf(Y)-1, -1}.
- You can find segment Y-2 by applying lower bound on the set bigElement for pair {leftBorderOf(Y-1)-1, -1}.
- You can find segment Y+1 by applying lower bound on the set smallElement for pair {rightBorderOf(Y)+1, -1}.
- You can find segment Y+2 by applying lower bound on the set bigElement for pair {rightBorderOf(Y+1)+1, -1}.
- Note we are able to compute these segments in this way because they are continuous.
-
Note there are X's where some segments might not exist(example if segment Y = [l, N] then both segment Y+1 and Y+2 will not exist) so you have to handle those too
 .
.
In case there are some doubts regarding implementation then you can refer to the editorialist’s code. I have commented it, so it might help.
TIME COMPLEXITY:
- For each test case, we are sorting the sequence requiring O(N*\log(N)). Now for each element, we are finding 5 segments, modifying smallElement set and bigElement set each requiring O(\log(N)) time and there are total N elements. So total time complexity per each test case is O(N*\log(N)).
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
#define int long long
#define p pair<int,int>
using namespace std;
char input[] = "input/input04.txt";
char output[] = "output/output04.txt";
int a[100010];
bool vis[100010];
int solve(p front, p curr, p back, int val, int n)
{
int ans = 0;
int x,y,z,u,v,temp;
x = curr.first - front.second - 1;
y = curr.second - curr.first + 1;
z = back.first - curr.second - 1;
if(front.first == 0)
u = 0;
else
u = front.second - front.first + 1;
if(back.second == n+1)
v = 0;
else
v = back.second - back.first + 1;
// cout << front.first << " " << front.second << endl;
// cout << curr.first << " " << curr.second << endl;
// cout << back.first << " " << back.second << endl;
// cout << val << endl;
// cout << x << " " << y << " " << z << " " << u << " " << v << endl;
if(y <= x+z)
{
if(y <= x && y <= z)
ans += (y+1);
else if(y > x && y <= z)
ans += (x+1);
else if(y <= x && y > z)
ans += (z+1);
else
ans += (x+z-y)+1;
}
// cout << "ans " << ans << endl;
temp = val - curr.first + 1;
if(val < curr.second && temp <= x)
{
temp = x - temp;
int temp1 = curr.second - val - 1;
ans += min(temp, temp1) + 1;
}
// cout << "ans " << ans << endl;
temp = curr.second - val + 1;
if(curr.first < val && temp <= z)
{
temp = z - temp;
int temp1 = val - curr.first - 1;
ans += min(temp, temp1) + 1;
}
// cout << "ans " << ans << endl;
temp = val - curr.first + 1;
if(u > 0 && x > temp && x <= u + y)
{
temp = x - temp - 1;
if(temp <= (u - 1) && temp <= (curr.second - val))
ans += (temp + 1);
else if(temp > (u - 1) && temp <= (curr.second - val))
ans += u;
else if(temp <= (u - 1) && temp > (curr.second - val))
ans += (curr.second - val + 1);
else
ans += (u + curr.second - val - temp);
}
// cout << "ans " << ans << endl;
temp = curr.second - val + 1;
if(v > 0 && z > temp && z <= v + y)
{
temp = z - temp - 1;
if(temp <= (v - 1) && temp <= (val - curr.first))
ans += (temp + 1);
else if(temp > (v - 1) && temp <= (val - curr.first))
ans += v;
else if(temp <= (v - 1) && temp > (val - curr.first))
ans += (val - curr.first + 1);
else
ans += (v + val - curr.first - temp);
}
// cout << "ans " << ans << endl;
return ans;
}
int32_t main()
{
// freopen(input, "r", stdin);
// freopen(output, "w", stdout);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
vector <p > v;
for(int i=1;i<=n;i++)
{
cin >> a[i];
v.push_back({a[i], i});
vis[i] = false;
}
sort(v.begin(), v.end());
set <p > s;
s.insert({0,0});
s.insert({n+1,n+1});
int ans = 0;
for(auto i:v)
{
vis[i.second] = true;
p front = {0, 0};
p back = {n+1, n+1};
p curr = {i.second, i.second};
if(i.second > 1)
{
if(vis[i.second-1])
{
auto temp = --s.lower_bound(curr);
front = *temp;
if(front.first >= 1)
{
curr.first = front.first;
s.erase(temp);
}
}
front = *(--s.lower_bound(curr));
}
if(i.second < n)
{
if(vis[i.second+1])
{
auto temp = s.lower_bound(curr);
back = *temp;
if(back.second <= n)
{
curr.second = back.second;
s.erase(temp);
}
}
// for(auto i:s)
// cout << i.first << " " << i.second << endl;
// cout << curr.first << " " << curr.second << endl;
back = *s.lower_bound(curr);
// cout << back.first << " " << back.second << endl;
}
s.insert(curr);
ans += solve(front, curr, back, i.second, n);
// cout << "ans " << ans << endl;
}
cout << ans << endl;
}
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#ifndef rd
#define trace(...)
#define endl '\n'
#endif
#define pb push_back
#define fi first
#define se second
// #define int long long
typedef long long ll;
typedef long double f80;
#define double long double
#define pii pair<int,int>
#define pll pair<ll,ll>
#define sz(x) ((long long)x.size())
#define fr(a,b,c) for(int a=b; a<=c; a++)
#define rep(a,b,c) for(int a=b; a<c; a++)
#define trav(a,x) for(auto &a:x)
#define all(con) con.begin(),con.end()
const ll infl=0x3f3f3f3f3f3f3f3fLL;
const int infi=0x3f3f3f3f;
const int mod=998244353;
//const int mod=1000000007;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef tree<pii, null_type, less<pii>, rb_tree_tag, tree_order_statistics_node_update> oset;
auto clk=clock();
mt19937_64 rang(chrono::high_resolution_clock::now().time_since_epoch().count());
int rng(int lim) {
uniform_int_distribution<int> uid(0,lim-1);
return uid(rang);
}
int powm(int a, int b) {
int res=1;
while(b) {
if(b&1)
res=(res*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return res;
}
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
int a[100005];
int sum_n=0;
void solve() {
int n=readIntLn(1,100000);
sum_n+=n;
set<int> lol1,lol2;
vector<pii> lol;
lol1.insert(0);
lol2.insert(0);
lol2.insert(n+1);
fr(i,1,n) {
if(i!=n)
a[i]=readIntSp(1,1000000000);
else
a[i]=readIntLn(1,1000000000);
lol.pb({a[i],i});
lol1.insert(lol1.end(),i);
}
lol1.insert(n+1);
sort(all(lol));
ll ans=0;
for(auto i:lol) {
int left,right;
int lefth,righth;
auto it=lol1.lower_bound(i.se);
it=lol1.erase(it);
right=(*it)-i.se-1;
if((*it)!=n+1)
righth=(*lol2.upper_bound(*it))-(*it);
else
righth=0;
it--;
left=i.se-(*it)-1;
if(*it)
lefth=(*it)-(*(--lol2.lower_bound(*it)));
else
lefth=0;
ans-=min(left,lefth)+min(right,righth);
int centre=left+right+1;
ans+=min(centre,lefth)+min(centre,righth);
ans+=max(0,min({lefth+righth+1-centre,lefth,righth,centre-1}));
lol2.insert(i.se);
}
reverse(all(lol));
lol1.swap(lol2);
for(auto i:lol) {
int left,right;
int lefth,righth;
auto it=lol1.lower_bound(i.se);
it=lol1.erase(it);
right=(*it)-i.se-1;
if((*it)!=n+1)
righth=(*lol2.upper_bound(*it))-(*it);
else
righth=0;
it--;
left=i.se-(*it)-1;
if(*it)
lefth=(*it)-(*(--lol2.lower_bound(*it)));
else
lefth=0;
int centre=left+right+1;
ans+=max(0,min({lefth+righth+1-centre,lefth,righth,centre-1}));
lol2.insert(i.se);
}
cout<<ans<<endl;
}
signed main() {
ios_base::sync_with_stdio(0),cin.tie(0),cout.tie(0);
srand(chrono::high_resolution_clock::now().time_since_epoch().count());
cout<<fixed<<setprecision(8);
int t=readIntLn(1,1000);
fr(i,1,t)
solve();
assert(1<=sum_n&&sum_n<=1000000);
assert(getchar()==EOF);
return 0;
}
Editorialist's Solution
// Please start reading the code from solveTestCase() function.
#include <bits/stdc++.h>
using namespace std;
int N;
set<pair<int, int>> smallElement, bigElement; // segments are stored as [Right Border, Left Border] to make the checking of intersection easier.
long long findWays(int idx) { // here idx is the index of current X
// let represent elements of greater than equal to idx by ******** and small by .........
long long ways = 0;
vector<pair<int, int>> seg(5, {-1, -1}); // the 5 segments are *******.......********.......******** where the segment 2(0-based indexing) contains idx.
// Note in the set the segments are stored as [Right Border, Left Border].
seg[2] = *bigElement.lower_bound(make_pair(idx, -1));
seg[1] = *smallElement.lower_bound(make_pair(seg[2].second-1, -1));
seg[3] = *smallElement.lower_bound(make_pair(seg[2].first+1, -1));
if((seg[1].first != seg[2].second-1) || (seg[1].first == 0) || (seg[1].first == N+1)) seg[1] = {-1, -1}; // segment not exist.
if((seg[3].second != seg[2].first+1) || (seg[3].second == N+1) || (seg[3].second == N+1)) seg[3] = {-1, -1}; // segment not exist.
if(seg[1].first != -1) {
seg[0] = *bigElement.lower_bound(make_pair(seg[1].second-1, -1));
}
if(seg[3].first != -1) {
seg[4] = *bigElement.lower_bound(make_pair(seg[3].first+1, -1));
}
if((seg[0].first != seg[1].second-1) || (seg[0].first == 0) || (seg[0].first == N+1)) seg[0] = {-1, -1}; // segment not exist.
if((seg[4].second != seg[3].first+1) || (seg[4].second == N+1) || (seg[4].second == N+1)) seg[4] = {-1, -1}; // segment not exist.
for(int i = 0; i < 5; i ++) swap(seg[i].first, seg[i].second);// [Right Border, Left Border] ---> [Left Border, Right Border]
// Case 1 - ********[.........*********]........*********
if(seg[1].first != -1) {
int seg2_size = seg[2].second-seg[2].first+1;
int seg1_size = seg[1].second-seg[1].first+1;
int forcedSize = idx-seg[2].first+1; // as we have to include the element at idx
ways += (long long)max(min(seg2_size-forcedSize+1, seg1_size-forcedSize+1), 0);
}
// Case 2 - ********.........[*********........]*********
if(seg[3].first != -1) {
int seg2_size = seg[2].second-seg[2].first+1;
int seg3_size = seg[3].second-seg[3].first+1;
int forcedSize = seg[2].second-idx+1; // as we have to include the element at idx
ways += (long long)max(min(seg2_size-forcedSize+1, seg3_size-forcedSize+1), 0);
}
// Case 3 - [********.........*********]........*********
if(seg[0].first != -1) {
int seg2_size = seg[2].second-seg[2].first+1;
int seg1_size = seg[1].second-seg[1].first+1;
int seg0_size = seg[0].second-seg[0].first+1;
int forcedSize = (idx-seg[2].first+1)+1; // as we have to include the element at idx and 1 element of seg[0].
if((seg1_size <= seg0_size + seg2_size) && (seg1_size >= forcedSize)) {
int remainEle = seg1_size-forcedSize; // these will be taken from seg[0] and seg[2]. and we force to take atleast one element from seg[0]
seg2_size -= (idx-seg[2].first+1);
seg0_size -= 1;
int minTake = max(remainEle-seg2_size, 0); // minimum number of elements you can take from seg[0].
int maxTake = min(remainEle, seg0_size); // maximum number of elements you can take from seg[0].
ways += (long long)(maxTake-minTake+1);
}
}
// Case 4 - ********.........[*********........*********]
if(seg[4].first != -1) {
int seg2_size = seg[2].second-seg[2].first+1;
int seg3_size = seg[3].second-seg[3].first+1;
int seg4_size = seg[4].second-seg[4].first+1;
int forcedSize = (seg[2].second-idx+1)+1; // as we have to include the element at idx and 1 element of seg[4].
if((seg3_size <= seg2_size + seg4_size) && (seg3_size >= forcedSize)) {
int remainEle = seg3_size-forcedSize; // these will be taken from seg[2] and seg[4]. and we force to take atleast one element from seg[4]
seg2_size -= (seg[2].second-idx+1);
seg4_size -= 1;
int minTake = max(remainEle-seg2_size, 0); // minimum number of elements you can take from seg[4].
int maxTake = min(remainEle, seg4_size); // maximum number of elements you can take from seg[4].
ways += (long long)(maxTake-minTake+1);
}
}
// Case 5 - ********[.........*********........]*********
if((seg[1].first != -1) && (seg[3].first != -1)) {
int seg1_size = seg[1].second-seg[1].first+1;
int seg2_size = seg[2].second-seg[2].first+1;
int seg3_size = seg[3].second-seg[3].first+1;
int forcedSize = 2; // as we have to take one element from seg[1] and seg[3].
if((seg2_size <= seg1_size + seg3_size) && (seg2_size >= forcedSize)) {
int remainEle = seg2_size-forcedSize;
seg1_size -= 1;
seg3_size -= 1;
int minTake = max(remainEle-seg1_size, 0); // minimum number of elements you can take from seg[3].
int maxTake = min(remainEle, seg3_size); // maximum number of elements you can take from seg[3].
ways += (long long)(maxTake-minTake+1);
}
}
return ways;
}
void modifySets(int idx) { // function now add the current idx from big elements to small elements and modify the ranges accordingly
// modifying bigElement set.
{
pair<int, int> seg = *bigElement.lower_bound(make_pair(idx, -1)); // finding the segment which contains X.
bigElement.erase(seg);
int L = seg.second, R = seg.first;
if(L < idx) bigElement.insert(make_pair(idx-1, L)); // if there is some big elements to the left of X.
if(R > idx) bigElement.insert(make_pair(R, idx+1)); // if there is some big elements to the right of X.
}
// modifying smallElement set.
{
// here idx is the index of the X.
int L = idx, R = idx; // current segment to add (idx, idx)
// below I am checking if any range of type (l, idx-1) exist, and if it then
// I will merge it with (idx, idx).
pair<int, int> seg = *smallElement.lower_bound(make_pair(idx-1, -1));
if((seg.first == idx-1) && (seg.first != 0) && (seg.first != N+1)) {
smallElement.erase(seg);
L = seg.second;
}
// below I am checking if any range of type (idx+1, r) exist, and if it then
// I will merge it.
seg = *smallElement.lower_bound(make_pair(idx+1, -1));
if((seg.second == idx+1) && (seg.second != 0) && (seg.second != N+1)) {
smallElement.erase(seg);
R = seg.first;
}
smallElement.insert({R, L}); // adding to set.
}
}
void solveTestCase() {
smallElement.clear();
bigElement.clear();
long long ans = 0;
cin >> N;
vector<pair<int, int>> a(N);
for(int i = 0; i < N; i ++) {
cin >> a[i].first;
a[i].second = i+1;
}
bigElement.insert({N, 1});
bigElement.insert({N+1, N+1}); // dummy segment is added to make implementation easy.
bigElement.insert({0, 0}); // dummy segment is added to make implementation easy.
smallElement.insert({N+1, N+1}); // dummy segment is added to make implementation easy.
smallElement.insert({0, 0}); // dummy segment is added to make implementation easy.
sort(a.begin(), a.end());
// Question basically ask us to find number of segment of length 2*L such that it is possible to divide the segment into two halfs such that
// one half contains smallest L elements and the other half contains the largest L element. So if we fix the smallest element of the larger half and
// L, and compute it for each element it will help us to prevent overcounting.
for(int X = 0; X < N; X ++) { // Trying to find all the segment of different length with the smallest element of the larger half a[i].first
ans += findWays(a[X].second); // a[X].second = index of current X.
modifySets(a[X].second);
}
cout << ans << '\n';
}
int main() {
ios_base::sync_with_stdio(0); // fast IO
cin.tie(0);
cout.tie(0);
int testCase;
cin >> testCase;
for(int i = 1; i <= testCase; i ++) {
solveTestCase();
}
return 0;
}
Video Editorial
Feel free to share your approach. In case of any doubt or anything is unclear please ask it in the comment section. Any suggestions are welcomed. ![]()