PROBLEM LINKS :
Contest : Division 1
Contest : Division 2
Practice
Setter : Harendra Chhekur
Tester : Istvan Nagy
Editorialist : Anand Jaisingh
DIFFICULTY :
Easy Medium
PREREQUISITES :
Properties of Regular Graphs
PROBLEM :
You need to minimize the maximum degree of any node, in a graph consisting of N nodes and M edges, given the condition that the graph has to be connected, can contain self loops but not multiple edges.
QUICK EXPLANATION :
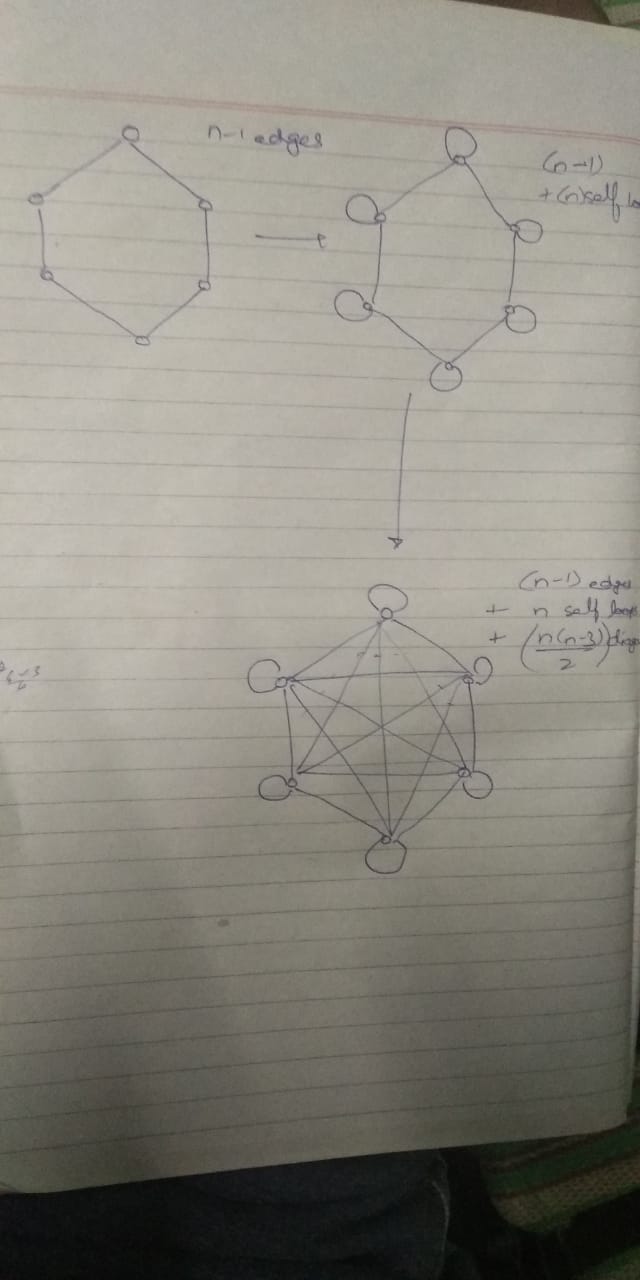
First, we consider a graph consisting of N nodes and 0 edges. Then, we can constructively incrementally build possible regular graphs on these N nodes. We can find a specific formula for finding the edge numbers where the maximum degrees grow, as we go from one possible regular graph to the next possible one.
EXPLANATION :
First of all, let’s try and resolve the case of when a valid graph exists, or does not. Some facts :
-
The minimum number of edges required to build a connected graph on n nodes is n-1, that will lead to a tree on these n nodes.
-
The maximum edges possible in a graph without multiple edges and self loops is \frac{n \cdot (n-1)}{2}, and if we add n self loops, the maximum number of edges transforms to \frac{n \cdot (n-1)}{2} + n = \frac{n \cdot (n+1)}{2} .
So, if M satisfies all these conditions in terms of n, then we’re good to go.
Definition :
Regular Graph : A k-regular graph on n nodes is a graph in which the degree of each node is the same and is k. A sufficient and necessary condition for the existence of a k-regular graph on n nodes is that n \cdot k \equiv 0 \mod 2
Now, we proceed as follows : We first consider that the graph cannot consist of self-loops, and for a given M and n, we build a graph with minimized maximum degree with Q=M-n edges, and in the end add n self loops to the graph.
Another fact of relevance is that the sum of degrees of all nodes in a graph consisting of Q edges is 2 \cdot Q . The strategy used to build an ideal graph is as follows : We select the largest k , such that n \cdot k \equiv 0 \mod 2 , and n \cdot k \le 2 \cdot Q
Then, we can build a k regular graph on these n nodes. Then, we proceed towards building a k+1 regular graph, but we don’t build it completely, we just keep on adding edges until the number of them remains \le Q .
To build a k regular graph on n nodes, we need to consider 2 special cases, these are :
Case 1 :
If k is even, we put all the vertices around a circle, and join each to its \frac{k}{2} nearest neighbors on each side.
Case 2 :
If k is odd, and n is even, we put the verties on a circle, join each to its \left\lfloor{\frac{k}{2}}\right\rfloor neighbors on each side, and also to the vertex directly opposite.
Before we move to some general formula, we should look out for some edge cases, like n=1 ,n=2 or n-1 \le M \le 2 \cdot n .
If n-1 \le M \le n+1 then we build a connected tree, with max degree 2 and since a tree always has at least 2 leaves, we add self loops to those leaves. So, the answer in this case remains 2.
If n+2 \le M \le 2 \cdot n -1 , then we first build a tree of max degree 2 , and then we keep on adding self-loops, and the answer in this case is 3.
Claim :
The answer for a graph consisting of n and M edges ( excluding the edge cases we handled above ) is always \left\lceil{ \frac{2 \cdot (M-n)}{n} }\right\rceil +1 .
Now, It’s better not to get into some rigorous proof here, and instead give you some intuition. For example consider the case n=9, M=31 .
We first build a 4-regular graph on these 9 vertices. This contributes 36 to the overall sum of degrees. Then, we can select 4 pairs, each of them disjoint, and then connect them. This is always possible. This contributes 8 to the overall degree. The sum of degrees is now 44, and the max degree is now 5 = \left\lceil{\frac{2 \cdot (M-n)}{n}}\right\rceil. Then we add 9 self loops, making the total number of edges 31, and the max degree 6.
Simulating more cases will help you more. For example, consider another one :
n=10, M=40 ,
We first build a 6 regular graph on these 10 vertices that contributes 60 to the overall degree, and 6 = \left\lceil{\frac{2 \cdot (M-n)}{n}}\right\rceil . The degree of each vertex is 6, and then we add 10 self loops, making the number of edges 40, and the max degree 7.
That’s it, thank you
Your Comments are Welcome !
COMPLEXITY ANALYSIS :
Time Complexity : O(T)
Space Complexity: O(1)
SOLUTION LINKS :
Setter
#include<iostream>
#include<cmath>
using namespace std;
int main(void){
int t;cin>>t;
while(t--){
long n,m;cin>>n>>m;
long max_poss_con = ((n * (n - 1)) / 2) + n;
if((m < n - 1) || (m > max_poss_con)) {
cout<<"-1\n";
continue;
}
if (n == 1 && m == 0){
cout <<"0\n";
continue;
}
if((n == 1) || (n == 2 && m == 1)){
cout<<"1\n";
continue;
}
long right = n / 2;
long left = n - right;
long d2 = n + 1;
long d3 = d2 + (n - 2) + 1;
if(m <= d2){
cout<<"2\n";
continue;
}else if(m <= d3){
cout<<"3\n";
continue;
}else{
if(n & 1){
long r = ceil(((m * 1.0) - d3) / (left + right));
long dl = (r * right) + ((r - 1) * left) + d3;
long du = (r * (left + right)) + d3;
if(m <= dl) cout<<r + r - 1 + 3<<"\n";
else cout<<r + r + 3<<"\n";
}else{
long d = ceil(((m - d3) / (left * 1.0) ) + 3);
cout<<d<<"\n";
}
}
}
}
Tester
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rall(x) (x).rbegin(), (x).rend()
#define forn(i, n) for (int i = 0; i < (int)(n); ++i)
#define for1(i, n) for (int i = 1; i <= (int)(n); ++i)
#define ford(i, n) for (int i = (int)(n) - 1; i >= 0; --i)
#define fore(i, a, b) for (int i = (int)(a); i <= (int)(b); ++i)
template<class T> bool umin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool umax(T &a, T b) { return a < b ? (a = b, true) : false; }
using namespace std;
int main(int argc, char** argv)
{
#ifdef HOME
if (IsDebuggerPresent())
{
freopen("../in.txt", "rb", stdin);
freopen("../out.txt", "wb", stdout);
}
#endif
int T, N, M;
scanf("%d", &T);
for (int tc = 0; tc < T; ++tc)
{
scanf("%d %d", &N, &M);
if (N == 1)
{
if(M < 2)
printf("%d\n",M);
else
printf("-1\n");
}
else if (N == 2)
{
if (M == 0 || M > 3)
printf("-1\n", M);
else if(M == 1)
printf("1\n");
else
printf("2\n");
}
else if (M + 1 < N || M > static_cast<int64_t>(N)*(N+1)/2)
{
printf("-1\n");
}
else
{
if (M <= N + 1)
M = 2;
else if (M <= N + N - 1)
M = 3;
else
M = (2 * M + N - 1) / N - 1;
printf("%d\n",M);
}
}
return 0;
}
Editorialist
//#pragma GCC optimize("Ofast,no-stack-protector")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx")
//#pragma GCC target("avx,tune=native")
// Anand Jaisingh
#include<bits/stdc++.h>
using namespace std;
typedef complex<double> base;
typedef long double ld;
typedef long long ll;
#define pb push_back
#define pii pair<int,int>
#define pll pair< ll , ll >
#define vi vector<int>
#define vvi vector< vi >
const int maxn=(int)(2e5+5);
const ll mod=(ll)(1e9+7);
int a[maxn];
int main()
{
//ios_base::sync_with_stdio(0);cin.tie(0);
int t;scanf("%d",&t);
while(t>0)
{
ll N,M;scanf("%lld %lld",&N,&M);
if (N == 1)
{
if(M < 2)
printf("%lld\n",M);
else
printf("-1\n");
}
else if (N == 2)
{
if (M == 0 || M > 3)
printf("-1\n");
else if(M == 1)
printf("1\n");
else
printf("2\n");
}
else if (M + 1 < N || M > static_cast<int64_t>(N)*(N+1)/2)
{
printf("-1\n");
}
else
{
if(M<=N+1)
{
printf("%d\n",2);
}
else if(M<=2*N-1)
{
printf("%d\n",3);
}
else
{
ll now=2ll*(M-N)+N-1,res=(now/N)+1;
printf("%lld\n",res);
}
}
t--;
}
return 0;
}