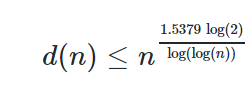Can you prove the time complexity of your solution?
Do you know the O(N\log N) solution which runs in 0.05s?
PROBLEM LINK:
Practice
Div-2 Contest
Div-1 Contest
Author: Ritesh Gupta
Tester: Radoslav Dimitrov
Editorialist: William Lin
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Math, Basic Geometry, Basic Number Theory
PROBLEM:
We are given several distinct points on the x-axis and the y-axis. Find the number of right triangles which can be formed from those points.
NOTE
Throughout this editorial, I will also use N to describe the maximum possible absolute value of the coordinates as well.
QUICK EXPLANATION
First, check if there is a point at (0, 0) and handle this case separately. The other triples which can form right triangles are of the form (-x_i, x_j, y_k) such that y_k^2=x_i x_j and (-y_i, y_j, x_k) such that x_k^2=y_i y_j. Consider the first type of triplet (-x_i, x_j, y_k), since the other type is similar.
QUICK EXPLANATION 1:
We will generate all factors of y_k^2 \le 10^5 and those will be our candidates for x_i to test. We can prove that this runs in O(N\sqrt{N}).
QUICK EXPLANATION 2:
Let g=\gcd(x_i, x_j), x_i=ga^2, and x_j=gb^2. Let’s iterate over all coprime pairs (a, b), then iterate over g. Then, we check if there exists x_i=ga^2, x_j=gb^2, and y_k=gab. We can prove that this runs in O(N\log N).
EXPLANATION:
First, check if there is a point at (0, 0). If there is, then that point cannot form a right triangle with two other points on the same axis (they would form a line). That point will only form a right triangle with another point on the x-axis and another point on the y-axis. There are N ways to choose the point on the x-axis and M ways to choose the point on the y-axis (N and M after removing (0, 0)), so we add N\cdot M to the answer.
Then, we somehow need to check if three points can form a right triangle. The three points cannot lie on the same axis, we either select two points from the x-axis or one point from the x-axis. Both cases are similar, so from now on, we will only consider the first case.
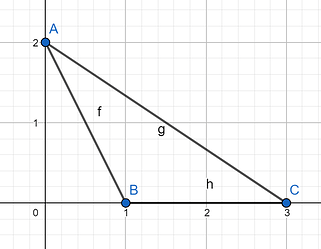
Observation 1. The two points cannot have the same sign.
Proof
Let’s draw a diagram:
The point on the x-axis closest to the origin will always have an obtuse angle, so forming a right triangle is impossible.
Thus, we know the triplets are of the form (-x_i, x_j, y_k).
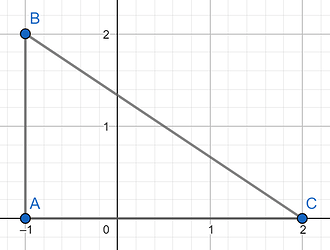
Observation 2. Only the point on the y-axis can have a right angle.
Proof
In order for a point on the x-axis to have a right angle, we need the points to be like this:
However, it’s impossible since we need a point to be on the y-axis.
Next, we will use a well-known theorem relating the altitude of a right triangle with the two parts of the hypotenuse.
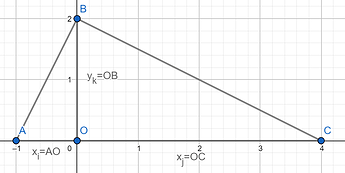
Observation 3. The condition for (-x_i, x_j, y_k) to form a right triangle is y_k^2=x_i x_j.
Proof
Triangles AOB and BOC are similar
Both of them share a right angle at O. Angles A and ABO are complementary, while angles ABO and OBC are complementary, so angle A is congruent to angle OBC. By Angle-Angle similarity, the two triangles are similar.
As the triangles are similar, the ratio of the sides will be the same, so \frac{AO}{OB}=\frac{OB}{OC}. Cross-multiplying and substituting, we get y_k^2=x_i x_j.
The rest of the solution is basically finding the number of triples which satisfy the condition. We should first calculate the frequency array of the coordinates, for each of positive x, negative x, positive y, and negative y. The rest of the solution can be done in several ways. Two of the simplest ways are listed below.
EXPLANATION 1:
We will iterate over all y_k. Notice that x_i must be a factor of y_k^2. Thus, to find all possible candidates of x_i, we should find the factors of y_k^2 less than 10^5. The detailed steps are listed below:
- Prime factorize y_k.
- Find the prime factorization of y_k^2 by multiplying all exponents in the factorization of y_k by 2.
- Use a recursive function to generate all of the factors. At the i-th level in the recursion, we consider multiplying the current number by a power of the i-th prime in y_k. Details can be found in my code below. You can also check out Generating all divisors of a number using its prime factorization - GeeksforGeeks.
- Test each factor f. Use our frequency array to check if there exists a negative x coordinate at f and a postive x coordinate at \frac{y_k^2}{f}.
The idea of this solution is simple, and it seems to run fast enough by testing. However, the time complexity of this solution is harder to prove. This is a long challenge, so it doesn’t hurt to try submitting ![]()
Observation 4. Solution 1 runs in O(N \sqrt N).
Proof
Note that this is similar to the proof that the number of pairs 1\le i, j \le n such that i divides j is O(N \log N).
Let’s calculate, for each factor f, the number of times it is a factor of y_k^2. We need to prove that this total sum is O(N \sqrt N).
Let the prime factorization of f be p_1^{e_1}p_2^{e_2}\ldots and the prime factorization of y_k be p_1^{g_1}p_2^{g_2}\ldots. In order for f to be a factor, the condition \frac{e_i}{2}\le g_i must be satisfied. Since g_i is an integer, we can rewrite this as \left\lceil \frac{e_i}{2} \right\rceil \le g_i.
Let’s create a function h(f) which transforms f into p_1^{\left\lceil \frac{e_1}{2} \right\rceil}p_2^{\left\lceil \frac{e_2}{2} \right\rceil}\ldots. From the condition above, in order for f to divide y_k^2, h(f) must divide y_k.
Note that y_k \le N and we can approximate the number of possible y_k for a given f with the expression \frac{N}{h(f)}. Thus, the total sum is \sum_{i = 1}^{N} \frac{N}{h(i)}.
h(f) \ge \sqrt f since \sqrt f = p_1^{\frac{e_1}{2}}p_2^{\frac{e_2}{2}}\ldots. Thus, \frac{N}{h(i)} \le \frac{N}{\sqrt i} and we can instead focus on the sum \sum_{i = 1}^{N} \frac{N}{\sqrt i}.
We can approximate the sum with the integral \int_{1}^{N} \frac{N}{\sqrt x} dx, which turns out to be O(N \sqrt N).
EXPLANATION 2:
Like other counting problems involving divisors, we can try iterating over the gcd.
Let g=\gcd(x_i, x_j), x_i=gc, and x_j=gd.
Observation 5. In order for x_i and x_j to form a triple, c and d must be perfect squares.
Proof
We know that x_i x_j = g^2cd = y_k^2, which is a perfect square. This also means that cd is a perfect square, meaning that each prime appears an even number of times. Note that c and d are relatively prime (we removed the gcd of x_i and x_j), so each prime also appears an even number of times in c or d. Thus, c and d are perfect squares.
Let’s rewrite c=a^2 and d=b^2. Now we have x_i=ga^2, x_j=gb^2, and y_k=gab. Now, we just have to iterate over all possible g, a, and b and check if all points in the triple exist with our frequency array. The details are below:
- Iterate over a from 1 to \sqrt N.
- Iterate over b from 1 to \sqrt N.
- If a and b are not coprime, then skip this pair as it contradicts our assumption.
- Iterate over g from 1 until g\cdot max(a, b)^2 reaches over N.
- Check that the points in the triple exist, using our frequency array.
This solution also seems to work fast, and its time complexity is interesting to prove.
Observation 6. Solution 2 runs in O(N \log N) time.
Proof
Let i=max(a, b). For a given pair (a, b), the innermost loop will run about \frac{N}{i^2} times.
The number of pairs such that max(a, b)=i is O(i).
Proof
We can consider the cases a\le b and a > b separately. When a\le b, b=i, so the pairs are of the form (a, i), and there are i possible choices for a.
When a>b, a=i, so the pairs are of the form (i, b), and there are i-1 possible choices for b.
In total, there are at most 2i-1 pairs.
For a single i, the number of iterations is O(i\cdot \frac{N}{i^2})=O(\frac{N}{i}).
The total time will just be the sum over all i, which is \sum_{i = 1}^{N} \frac{N}{i}.
This is well-known in Competitive Programming to be equal to O(N \log N).
Proof
We can approximate the sum with the integral \int_{1}^{N} \frac{N}{x} dx.
SOLUTIONS:
Setter's Solution
#include <bits/stdc++.h>
#define endl '\n'
#define SZ(x) ((int)x.size())
#define ALL(V) V.begin(), V.end()
#define L_B lower_bound
#define U_B upper_bound
#define pb push_back
char input[] = "input/input07.txt";
char output[] = "output00.txt";
using namespace std;
template<class T, class T1> int chkmin(T &x, const T1 &y) { return x > y ? x = y, 1 : 0; }
template<class T, class T1> int chkmax(T &x, const T1 &y) { return x < y ? x = y, 1 : 0; }
const int MAXN = (1 << 17);
int n, m;
int x[MAXN], y[MAXN];
int lp[MAXN];
bool zeroFlag;
void read() {
cin >> n >> m;
zeroFlag = false;
for(int i = 0; i < n; i++) {
cin >> x[i];
if(x[i] == 0) {
i--;
n--;
zeroFlag = true;
}
}
for(int i = 0; i < m; i++) {
cin >> y[i];
if(y[i] == 0) {
i--;
m--;
zeroFlag = true;
}
}
}
void gen(vector<pair<int, int> > &p, vector<int64_t> &li, int i = 0, int64_t X = 1) {
if(X >= MAXN) {
return;
}
if(i == SZ(p)) {
li.push_back(X);
return;
}
int64_t PASD = 1;
for(int l = 0; l <= p[i].second; l++) {
gen(p, li, i + 1, X * PASD);
PASD *= p[i].first;
}
}
int cnt[2 * MAXN + 42];
int64_t solve_one() {
for(int i = 0; i < 2 * MAXN + 42; i++) {
cnt[i] = 0;
}
for(int i = 0; i < m; i++) {
cnt[y[i] + MAXN]++;
}
int64_t answer = 0;
for(int i = 0; i < n; i++) {
int o = max(-x[i], x[i]);
vector<pair<int, int> > vec;
while(o > 1) {
int c = 0, d = lp[o];
while(o % d == 0) {
o /= d;
c++;
}
vec.pb({d, c << 1});
}
vector<int64_t> li;
gen(vec, li, 0, 1ll);
for(int64_t v: li) {
int64_t q = x[i] * 1ll * x[i] / v;
if(q < MAXN) {
answer += cnt[q + MAXN] * 1ll * cnt[MAXN - v];
}
}
}
return answer;
}
void solve() {
int64_t ans = 0;
if(zeroFlag)
ans += n * 1LL * m;
ans += solve_one();
swap(n, m);
for(int i = 0; i < max(n, m); i++) {
swap(x[i], y[i]);
}
ans += solve_one();
cout << ans << endl;
}
void prepare() {
for(int i = 2; i < MAXN; i++) {
for(int j = i; j < MAXN; j += i) {
if(lp[j] == 0) lp[j] = i;
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
// freopen(input, "r", stdin);
// freopen(output, "w", stdout);
prepare();
int T;
cin >> T;
while(T--) {
read();
solve();
// std::vector<int64_t> li;
// std::vector<pair <int,int> > vec;
// vec.push_back({2,3});
// vec.push_back({3,1});
// gen(vec, li, 0, 1ll);
// for(int i:li)
// cout << i << " ";
// cout << endl;
}
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
#define endl '\n'
#define SZ(x) ((int)x.size())
#define ALL(V) V.begin(), V.end()
#define L_B lower_bound
#define U_B upper_bound
#define pb push_back
using namespace std;
template<class T, class T1> int chkmin(T &x, const T1 &y) { return x > y ? x = y, 1 : 0; }
template<class T, class T1> int chkmax(T &x, const T1 &y) { return x < y ? x = y, 1 : 0; }
const int MAXN = (1 << 18);
int n, m;
int x[MAXN], y[MAXN];
int lp[MAXN];
int cnt_zeroes = 0;
void read() {
cin >> n >> m;
cnt_zeroes = 0;
for(int i = 0; i < n; i++) {
cin >> x[i];
if(x[i] == 0) {
i--;
n--;
cnt_zeroes++;
}
}
for(int i = 0; i < m; i++) {
cin >> y[i];
if(y[i] == 0) {
i--;
m--;
cnt_zeroes++;
}
}
}
void gen(vector<pair<int, int> > &p, vector<int64_t> &li, int i = 0, int64_t X = 1) {
if(X >= MAXN) {
return;
}
if(i == SZ(p)) {
li.push_back(X);
return;
}
int64_t PASD = 1;
for(int l = 0; l <= p[i].second; l++) {
gen(p, li, i + 1, X * PASD);
PASD *= p[i].first;
}
}
int cnt[2 * MAXN + 42];
int64_t solve_one() {
for(int i = 0; i < 2 * MAXN + 42; i++) {
cnt[i] = 0;
}
for(int i = 0; i < m; i++) {
cnt[y[i] + MAXN]++;
}
int64_t answer = 0;
for(int i = 0; i < n; i++) {
int o = max(-x[i], x[i]);
vector<pair<int, int> > vec;
while(o > 1) {
int c = 0, d = lp[o];
while(o % d == 0) {
o /= d;
c++;
}
vec.pb({d, c << 1});
}
vector<int64_t> li;
gen(vec, li, 0, 1ll);
for(int64_t v: li) {
int64_t q = x[i] * 1ll * x[i] / v;
if(q < MAXN) {
answer += cnt[q + MAXN] * 1ll * cnt[MAXN - v];
}
}
}
return answer;
}
void solve() {
int64_t ans = solve_one();
if(cnt_zeroes) {
ans += cnt_zeroes * 1ll * n * 1ll * m;
}
swap(n, m);
for(int i = 0; i < max(n, m); i++) {
swap(x[i], y[i]);
}
ans += solve_one();
cout << ans << endl;
}
void prepare() {
for(int i = 2; i < MAXN; i++) {
for(int j = i; j < MAXN; j += i) {
if(lp[j] == 0) lp[j] = i;
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
prepare();
int T;
cin >> T;
while(T--) {
read();
solve();
}
return 0;
}
Editorialist's Solution 1
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mxN=1e5;
//greatest prime factor
int gp[mxN+1];
int n, m, x[mxN], y[mxN];
int c[2][mxN+1];
ll ans;
void dfs(vector<array<int, 2>> &pf, vector<int> &f, int i=0, ll x=1) {
if(i>=pf.size()||x*pf[i][0]>mxN) {
f.push_back(x);
return;
}
//multiply x by p^j
for(int j=0; j<=2*pf[i][1]&&x<=mxN; x*=pf[i][0], ++j)
dfs(pf, f, i+1, x);
}
void solve2(int n, int x[mxN], int m, int y[mxN]) {
//store y in frequency array
memset(c, 0, sizeof(c));
for(int i=0; i<m; ++i)
++c[y[i]<0][abs(y[i])];
for(int i=0; i<n; ++i) {
//prime factorize x[i]
//stored as pairs (prime, exponent)
vector<array<int, 2>> pf;
int x2=abs(x[i]);
while(x2>1) {
int p=gp[x2], c=0;
while(x2%p==0) {
x2/=p;
++c;
}
pf.push_back({p, c});
}
//make pf in increasing order
reverse(pf.begin(), pf.end());
//generate all factors of x[i]^2 <= mxN
vector<int> f;
dfs(pf, f);
//test each factor
for(int j : f)
if((ll)x[i]*x[i]/j<=mxN)
ans+=c[0][j]*c[1][(ll)x[i]*x[i]/j];
}
}
void solve() {
//input
cin >> n >> m;
bool zero=0;
for(int i=0; i<n; ++i) {
cin >> x[i];
if(!x[i]) {
zero=1;
--i;
--n;
}
}
for(int i=0; i<m; ++i) {
cin >> y[i];
if(!y[i]) {
zero=1;
--i;
--m;
}
}
ans=(ll)zero*n*m;
//count triples (x, y, y)
solve2(n, x, m, y);
//count triples (y, x, x)
solve2(m, y, n, x);
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
//sieve
for(int i=2; i<=mxN; ++i)
if(!gp[i])
for(int j=0; (j+=i)<=mxN; )
gp[j]=i;
int t;
cin >> t;
while(t--)
solve();
}
Editorialist's Solution 2
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mxN=1e5;
int n, m, x[mxN], y[mxN];
int c1[mxN+1], c2[2][mxN+1];
ll ans;
void solve2(int n, int x[mxN], int m, int y[mxN]) {
//put x and y in frequency arrays
memset(c1, 0, sizeof(c1));
for(int i=0; i<n; ++i)
++c1[abs(x[i])];
memset(c2, 0, sizeof(c2));
for(int i=0; i<m; ++i)
++c2[y[i]<0][abs(y[i])];
for(int a=1; a*a<=mxN; ++a)
for(int b=1; b*b<=mxN; ++b)
if(__gcd(a, b)<2)
for(int g=1; max((ll)g*a*a, (ll)g*b*b)<=mxN; ++g)
ans+=c1[g*a*b]*c2[0][g*a*a]*c2[1][g*b*b];
}
void solve() {
//input
cin >> n >> m;
bool zero=0;
for(int i=0; i<n; ++i) {
cin >> x[i];
if(!x[i]) {
zero=1;
--i;
--n;
}
}
for(int i=0; i<m; ++i) {
cin >> y[i];
if(!y[i]) {
zero=1;
--i;
--m;
}
}
ans=(ll)zero*n*m;
//count triples (x, y, y)
solve2(n, x, m, y);
//count triples (y, x, x)
solve2(m, y, n, x);
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()