CHEFRAIL - Editorial

editorial
, , , , , ,
6

I used the fact that multiplication of prime factors of xi whose frequency is odd will pair with xj with same multiplication of prime factors whose frequency is odd.
Here is my solution: CodeChef: Practical coding for everyone

3 Likes
7

No, it says in the problem description that all stations are distinct.

1 Like
8

Another fun fact :
totalDivs = 0;
for( i = 1; i <= 100000; i++)
totalDivs += numberOfDivisors(i*i);

Now totalDivs <= 10^7

So without any complex mathematical prove, you can have an idea that you will need to perform number of operations proportional to 10^7 if you wish to find all the divisors using the prime factorizations of i^2.

1 Like
9

The number theoretic explanation is too good.

2 Likes
10

I find it helpful so sharing it here.

4 Likes
12

iterate g from 1 to g*max(a,b)^2 untill it reach N…I dont understand this constraint.

13

Thanks for sharing, I have included it.

1 Like
14

Something like

for(int g=1; g*max(a, b)*max(a, b)<=N; ++g) {
}
2 Likes
16

ok i got it, but also i think that the fact that a and b are relatively prime is not used in proving the time complexity…so i think it will be somewhat less then O(NlogN) as the entire inner loop will get skipped if gcd(a,b)>2. probably O(Nloglog(N))

17

The upper bound for number of divisors is generally taken as O(n^1/3).

See this…

Also, the approach can be optimised, if we prune the recursion if the factor is getting larger than 10^5.

My solution took 0.35s. CodeChef: Practical coding for everyone

2 Likes
18

If someone has patience to waste their 9 minutes, can watch this XD

2 Likes
19

already watched it man xD

1 Like
20

problem with O(nrootn) solution is many got AC and many did not and got 40 points…and TLE in rest of the cases…including me…so dont trust o(nrootn) hahaha, This O(Nlogn) solution is very good. Kudos to @tmwilliamlin :slight_smile:

1 Like
21

What will be the time complexity for this ? and at max how many factors can it have ?

23

let d(n) be number of divisors of n,
d(n) <= sqrt(n) or to be more precise,
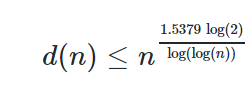
image

2 Likes
24

If someone can explain the time complexity, please do.

25

I used this Find all factors of a Natural Number - GeeksforGeeks
to generate divisors, it also takes O(NrootN)
My solution got TLE after 40 points, can someone suggest why?

26

Did you use fast io ?

27

Yes I did.
https://www.codechef.com/viewsolution/29664661

28

I think Quick Explanation 1 is enough to change 40 point solution to 100.
I was looping through all divisors.