CHEFRECT-Editorial

editorial
, , ,
1

PROBLEM LINK:

CHEFRECT

Author: aniket_111
Tester: sahoomirnalin
Editorialist: aniket_111

DIFFICULTY:

HARD

PREREQUISITES:

Basic mathematics, matrix, array.

PROBLEM:

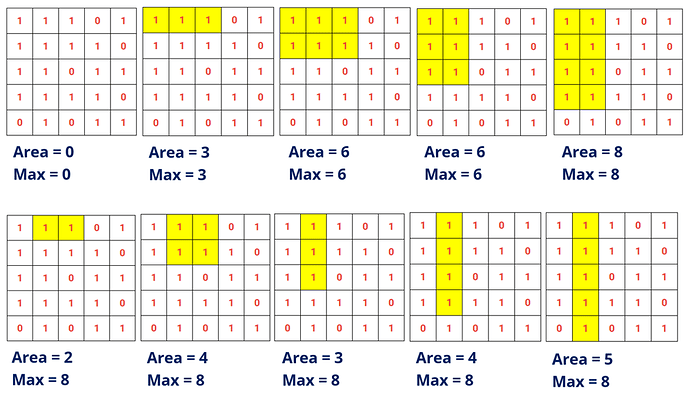
For a table in a restaurant which divided by n x m cells, the waiter has randomly placed Ice-cream and gulab jamun on each cell of the table. Find out the largest rectangle which can be formed by Ice-creams only such that there is no gulab jamun within the rectangle. Note: Ice-cream is represented by char values as ‘1’ and gulab jamun by ‘0’. The input is given in the form of n x m Matrix containing zeros and ones.

EXPLANATION

Instead of forming every rectangle, then checking validity of rectangle, we can optimize the brute-force by only considering valid rectangles. For this, we can start from every cell and consider valid rectangle starting from that cell.

  • Let the current cell be at (i, j).
  • We first consider ith row and find maximum column length of 1s starting from M[i][j].
  • Then move to i+1th row and find maximum column length of 1s starting from M[i+1][j]. Take minimum of all lengths and find the area and keep updating max area.
  • Continue similar process till you reach last row and then repeat the process for all other cells as well.
  • Finally return maximum area found from all valid rectangles.
    image
    image1000×572 99.8 KB

TIME COMPLEXITY

Time complexity is O((mn)^2)

SOLUTIONS:

#include <iostream>
#include<bits/stdc++.h>
using namespace std;

int maximalRectangle(vector<vector<char>>& M) {
        if(!size(M)) return 0;
        int ans = 0, m = size(M), n = size(M[0]);
        for(int i = 0; i < m; i++) 
            for(int j = 0; j < n; j++) 
                for(int row = i, colLen = n, col; row < m && M[row][j] == '1'; row++) {
                    for(col = j; col < n && M[row][col] == '1'; col++);
                    colLen = min(colLen, col-j);
                    ans = max(ans, (row-i+1) * colLen);
                }
            
        return ans;
    }
    
int main() {
	// your code goes here
	int n,m,ans=0;
	char val;
	    vector<vector<char>> v2;
	    vector<char> v1;
	    cin>>n>>m;
	    for(int i=0;i<n;i++){
	        v1={};
	        for(int j=0;j<m;j++){
	            cin>>val;
	            v1.push_back(val);
	        }
	        v2.push_back(v1);
	    }
	    ans=maximalRectangle(v2);
	    cout << ans <<endl;
	
	return 0;
}