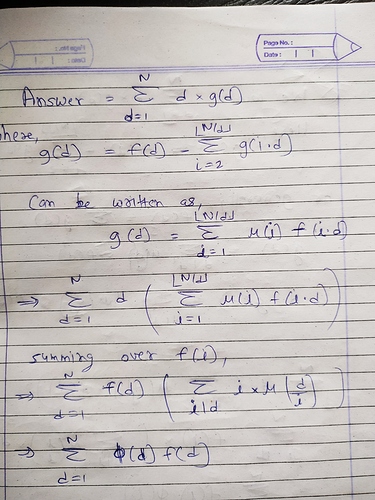PROBLEM LINK:
Author: Navneel Singhal
Tester: Suchan Park
Editorialist: Navneel Singhal
DIFFICULTY:
Hard
PREREQUISITES:
DP, sieve of Eratosthenes, modular exponentiation, prime compression, complexity analysis, constant optimization
PROBLEM:
You have a sequence of n numbers, a_1, a_2, \dots, a_n, all greater than 1. You are also given 3 integers k, m, x. Find the following value modulo 10^9 + 7.
\sum_{T \in \{1, 2, \dots, n\}^k} G(T) \cdot W(T) \cdot S_x(T) \cdot P_m(T)
The definitions of G, S_x, P_m, W are as follows:
G((i_1, \dots, i_k)) = \gcd(a_{i_1}, \dots, a_{i_k})
S_x((i_1, \dots, i_k)) = a_{i_1}^x + \dots + a_{i_k}^x
P_m((i_1, \dots, i_k)) = \left(a_{i_1} \cdots a_{i_k}\right)^m
W(T) = \mathrm{smallest\,\, prime\,\, divisor\,\, of\,\, } P_1(T)
QUICK EXPLANATION:
Iterate over possible values of G(T), and for each such value, compute the rest of the addend by considering it as a sum of polynomials. To improve upon the complexity, use a compressed way to store and loop over things, and perform some constant optimizations (fast IO, avoiding recomputing, reducing powers) to squeeze the solution into the time limit.
EXPLANATION:
Firstly we look at tuples with a common G value, say d. Then the summand becomes d \times g(d), where g(d) is the sum of W(T) \cdot S_x(T) \cdot P_m(T) over all tuples T which have G(T) = d.
Let f(d) be the sum of g(i \cdot d) over all positive integers i such that i\cdot d \le N (where N is the maximum value in the given sequence).
f(d) is basically the sum of g over all tuples whose G- values are divisible by d, so we will try to compute f(d), then use the values of g(i\cdot d) for i > 1 to compute g(d) = f(d) - \sum_{i = 2}^{\lfloor N/d\rfloor} g(i\cdot d). If we can find f(d), then the transition to g(d) can be done in N/d steps using a dp which stores the values of g, which starts from the largest value of d, and the total overhead would be \mathcal{O}(N \log N).
So our task is now to find f(d) efficiently. One thing we will do for this is making a frequency array \mathrm{freq}, where \mathrm{freq}_i tells us how many times the number i appears in the given sequence, and this can be done in O(n).
Now fix d. Suppose we have all elements which are divisible by d in an array with us, sorted in decreasing order of the smallest prime factor. Then we will have certain contiguous blocks of elements with each element in a given block having the same smallest prime factor (spf for short). Say the i^\mathrm{th} block is B_i with spf being s_i, and call its j^\mathrm{th} element h_{ij}. Let V_{i, \,e} denote the sum of the e^\mathrm{th} powers of elements in B_i.
Here’s the crucial observation: the sum of S_x(T) \cdot P_m(T) over all tuples T with G(T) being divisible by d and W(T) = s_i is exactly k \times ((V_{1,\, m} + \cdots + V_{i,\, m})^{k - 1}(V_{1,\, m+x} + \cdots + V_{i,\, m+x}) - (V_{1,\, m} + \cdots + V_{i-1,\, m})^{k - 1}(V_{1,\, m+x} + \cdots + V_{i-1,\, m+x}))
Let’s break the proof of this into small chunks. Firstly note that if you consider the value of o_1^{b+a}o_2^b\cdots o_k^b and rotate the associated tuple (o_1, o_2, \dots, o_k) k times and add this value for each rotated tuple, you get the sum (o_1^a + o_2^a + \cdots + o_k^a) \times (o_1^b \cdots o_k^b). Note that all our functions are invariant under this sort of a rotation, so if we replace S_x((i_1, \dots, i_k)) by a_{i_1}^x provided we multiply by k in the end, we are good to go.
Now if you look at the expression we claimed, it should be much clearer, because the first term generates the sum over all tuples whose spf is at least s_i, and the second term subtracts off the sum over all tuples whose spf is at least s_{i - 1}, proving our claim.
Now we can simply multiply this by s_i and add this over all the spfs to get f(d), from where our strategy is as outlined above.
Mathematically speaking, we are done, but let’s see how to implement this in a very efficient way.
Since we have already constructed the array \mathrm{freq}, we for every d, we should be able to get the elements that are divisible by d in \mathcal{O}(N/d) time. For the spf computation, we can precompute the spfs in \mathcal{O}(N \log \log N) using the sieve of Eratosthenes. Additionally, we will also be computing a vector containing all primes \le N in order, and the value of \pi(n) which denotes the number of primes \le n for all n \le N.
One nice property we will exploit is the following: if the G- value of some tuple T is divisible by d and d \ne 1, then the spf of the elements corresponding to that tuple will be the smaller of spf(d) and spf(element/d), if the element is not d itself. So we note that the number of spfs are at most \min(\pi(N/d), \pi(spf_d)) + 1, with the +1 being for the possibility that the spf is spf(d) (which arises in the case that the element itself is d).
We also note another cool thing: only the V- values of blocks are necessary, so if we precompute the values of \mathrm{freq}_i \cdot i^e for e = m, m + x, (which can be done in \mathcal{O}(N \log \mathrm{Mod}) by suitably reducing the exponent using x^p \equiv x \pmod p and using binary exponentiation), we can simply add them to the block values.
Hence, we can maintain \min(\pi(N/d), \pi(spf_d)) + 1 memory locations (as a couple of arrays of \min(\pi(N/d), \pi(spf_d)) members and O(1) more memory for the extra case, or just a global buffer) and for every multiple of d, add the precomputed values to each block in time O(N/d), we can get to the value of V_{i, e} (e = m, m + x) for each block, and the prefix sum computation along with the computation of f(d) will take time \mathcal{O}(\min(\pi(N/d), \pi(spf_d)) \log \mathrm{Mod}). (We do a similar thing in the case when d = 1).
So for a particular d, the time taken is \mathcal{O}(N/d + \min(\pi(N/d), \pi(spf_d)) \log \mathrm{Mod}). Using the fact that \pi(x) \sim \frac{x}{\log x} and using integration, we can show that the sum of all these turns out to be \mathcal{O}(N \log N + N \log \log N \log \mathrm{Mod}) if we ignore the \min in there. The memory overhead for the computation of f(d) is always o(N).
Now since the total time complexity for the input, precomputation of freq, powers, pi function, spf, and the dp transitions sums up to \mathcal{O}(n + N \log \mathrm{Mod} + N \log \log N + N \log N), the final time complexity is \mathcal{O}(n + N \log N + N \log \log N \log \mathrm{Mod}), with a good speedup due to the \min which we left out (I suspect that we can replace the \log \log N factor by 1; for an empirical discussion of this, see the last paragraph). The space complexity is \mathcal{O}(N).
Some of the following optimizations are necessary to get the solution to pass (you probably don’t need all of them)
-
Fast input-output (standard unsyncing of stdio and iostream works)
-
Precomputing the values as mentioned as well as minimizing multiplications/divisions in the two heavy phases that appear in the time complexity.
-
Reducing powers for exponentiation – this is quite important since it reduces the runtime by 3x
-
Using a vector of size \mathcal{O}(\pi(N/d)) and not \mathcal{O}(N/d) – this is needed otherwise the \log \log N factor is replaced by \log N which gives TLE. An analogous optimization needs to be done if you replace the vectors by storage in a global buffer as well.
-
Using old values to avoid computing the powers of the prefix sums of the V- values once again unnecessarily.
-
Taking the \min we left out in the complexity analysis into consideration by adjusting the solution suitably by checking for special cases as mentioned above.
Note: To do a slightly better complexity analysis, we can do the following:
Since we have spf_d \le d, we have \min(\pi(N/d), \pi(spf_d)) \le \min(\pi(N/d), \pi(d)) which is at most \pi(\sqrt{N}). Thus for each value of d which is less than \sqrt{N}, we get rid of at least about \pi(N/d) - \pi(\sqrt{N}) iterations, which roughly reduces to half the iterations right there. A more accurate analysis would take into account the distribution of each prime as the smallest prime factor, but this is enough to show the kind of speedup such an optimization gives us. (In fact, using a simulation, it was seen that the sum of \min(\pi(N/d), \pi(spf_d)) over d = 2 to N is practically N for values of N relevant for this problem (it might be different for general N), while the sum of \pi(N/d) is roughly N \ln \ln N). Thus a reasonable conjecture can be that the final complexity turns out to be \mathcal{O}(n + N \log N + N \log \mathrm{Mod}) (at least for such N).
Challenge
Is it possible to find a faster solution? Also, is it possible to prove the conjecture above or even just get a good bound mathematically? (It might not be true, because when N is increased, the graph is not that “linear”).
SOLUTIONS:
Setter's solution (C++)
/*
* @author Navneel Singhal
*/
#pragma GCC optimize("Ofast")
#include <iostream>
#include <vector>
#include <cassert>
#include <cstring>
using namespace std;
/*
* SOLUTION STARTS AT FUNCTION solve()
*/
/*
* Fast power function
*/
template <typename T>
T Power (T a, int n = 1, T id = 1) {
T ans = id;
while (n) {
if (n & 1) ans *= a;
a *= a;
n >>= 1;
}
return ans;
}
/*
* Struct for integers modulo a given prime modulus
*/
template <unsigned Mod = 998'244'353>
struct Modular {
using M = Modular;
unsigned v;
Modular(long long a = 0) : v((a %= Mod) < 0 ? a + Mod : a) {}
M operator-() const { return M() -= *this; }
M& operator+=(M r) { if ((v += r.v) >= Mod) v -= Mod; return *this; }
M& operator-=(M r) { if ((v += Mod - r.v) >= Mod) v -= Mod; return *this; }
M& operator*=(M r) { v = (uint64_t)v * r.v % Mod; return *this; }
M& operator/=(M r) { return *this *= power(r, Mod - 2); }
friend M operator+(M l, M r) { return l += r; }
friend M operator-(M l, M r) { return l -= r; }
friend M operator*(M l, M r) { return l *= r; }
friend M operator/(M l, M r) { return l /= r; }
friend bool operator==(M l, M r) { return l.v == r.v; }
friend bool operator!=(M l, M r) { return l.v != r.v; }
friend ostream& operator<<(ostream& os, M &a) { return os << a.v; }
friend istream& operator>>(istream& is, M &a) { int64_t w; is >> w; a = M(w); return is; }
};
const int mod = 1e9 + 7;
using mint = Modular<mod>;
const int maxa = 1e6 + 6;
/*
* spf[n] is the smallest prime factor of n, defined for n > 1
* pi[n] is the number of primes not exceeding n, defined for n >= 0
* primes[i] is the (i+1)th prime
*/
int spf[maxa], pi[maxa];
vector<int> primes;
/*
* precomputes the arrays spf and pi
*/
void precompute() {
memset(spf, -1, sizeof spf);
int pi_cur = 0;
pi[0] = pi[1] = 0;
for (int i = 2; i < maxa; i++) {
if (spf[i] == -1) { //i is prime
spf[i] = i;
pi_cur++;
primes.push_back(i);
if ((long long) i * i >= maxa) { //to prevent overflow in the next loop, as maxa is int
pi[i] = pi_cur;
continue;
}
//if x < i, then x * i's smallest prime factor is spf[x], which has already been computed, so we only need to update those multiples of i which are >= i * i
for (int j = i * i; j < maxa; j += i) {
if(spf[j] == -1) spf[j] = i;
}
}
pi[i] = pi_cur;
}
}
/*
* freq[i] = number of occurences of i in the input array
* Powm[i] = Power(i, m) * freq[i]
* Powx[i] = Power(i, m + x) * freq[i]
* dp[i] = g(d), if the answer to the problem is the sum of d * g(d) over all possible gcds d of tuples
*/
int freq[maxa];
mint dp[maxa], Powm[maxa], Powx[maxa];
vector<mint> vm, vx;
int reducePower (long long Power) {
int reducedPower = Power % (mod - 1);
if (reducedPower == 0 && Power != 0) {
reducedPower = mod - 1;
}
return reducedPower;
}
//overall time complexity : O(n + maxa * log(log(maxa)) * log(mod) + maxa * log(maxa))
//overall space complexity : O(maxa)
void solve (int case_no) {
//complexity : O(maxa * log(log(maxa)))
precompute();
vm.resize(pi[maxa - 1]);
vx.resize(pi[maxa - 1]);
long long k, M, X;
int n, y;
cin >> n >> k >> M >> X;
int k2 = reducePower(k - 1);
int m = reducePower(M);
int x = reducePower(X + m);
mint finans = 0;
//complexity : O(n)
for (int i = 0; i < n; ++i) {
cin >> y;
assert(y > 1); //spf is not defined for 0, 1
freq[y]++;
}
//complexity : O(maxa * log(mod))
for (int i = 0; i < maxa; ++i) {
Powm[i] = freq[i] * Power(mint(i), m);
Powx[i] = freq[i] * Power(mint(i), x);
}
//complexity : sum of pi(maxa/g) log(mod) + maxa/g = (maxa/g)/(log(maxa/g)) log(mod) + maxa/g, which turns out to be O(maxa * log(log(maxa)) * log(mod) + maxa * log(maxa))
for (int g = maxa - 1; g > 1; --g) { //handle g = 1 later on
int siz = pi[(maxa - 1) / g];
/*
* vm[i] contains the sum of Power(r, m) where r is divisible by g, and spf[r] is the ith prime, and vx[i] contains the sum of the corresponding (m + x)th Powers
* vgm is used to handle the case of r = g if spf[g] does not fit in this vector; this needs to be handled separately because spf[1] is not well defined
*/
mint vgm, vgx;
int spfg = spf[g];
//handled r = g here
bool extra = false;
int idx;
if (pi[spfg] > siz) {
if (freq[g] > 0) {
extra = true;
vgm = Powm[g];
vgx = Powx[g];
}
}
else {
if (freq[g] > 0) {
idx = pi[spfg] - 1;
//assert (idx >= 0 && idx < siz && true);
vm[idx] += Powm[g];
vx[idx] += Powx[g];
}
}
//handled r = any multiple of g more than g
//complexity : O(maxa/g)
for (int r = g << 1, w = 2; r < maxa; r += g, ++w) {
if (freq[r] == 0) continue;
idx = pi[min(spf[w], spfg)] - 1;
/*
* idx fits in the size of the array because siz = pi[(maxa - 1)/g] >= pi[r/g] = pi[w] >= pi[spf[w]]
*/
vm[idx] += Powm[r];
vx[idx] += Powx[r];
}
mint curm = 0, curx = 0, ans = 0, pold = 0, pcur = 0;
if (extra) { //this means spfg is larger than all the primes below (maxa - 1) / g, so we need to process spfg first
curm += vgm;
curx += vgx;
pold = pcur;
pcur = Power(curm, k2) * curx;
ans += spfg * (pcur - pold);
}
//complexity : O(pi(maxa/g) * log(mod)) - actually O(min(pi(maxa/g), pi(spfg)) * log(mod))
for (int i = min(pi[spfg], siz) - 1; i >= 0; --i) {
curm += vm[i];
curx += vx[i];
vm[i] = 0;
vx[i] = 0;
pold = pcur;
pcur = Power(curm, k2) * curx;
ans += primes[i] * (pcur - pold);
}
//complexity : O(maxa/g)
for (int d = g << 1; d < maxa; d += g) {
ans -= dp[d];
}
dp[g] = ans;
finans += g * ans;
}
/*
* handle g = 1 here
* here we note that spfg does not exist, and instead of min(spfg, spf[r]) we need spf[r]
*/
{
int g = 1, idx;
int siz = pi[(maxa - 1) / g];
//handled r = any multiple of g more than g
for (int r = g << 1, w = 2; r < maxa; r += g, ++w) { //how to handle r = g
idx = pi[spf[w]] - 1;
vm[idx] += Powm[r];
vx[idx] += Powx[r];
}
mint curm = 0, curx = 0, ans = 0, pold = 0, pcur = 0;
for (int i = siz - 1; i >= 0; --i) {
curm += vm[i];
curx += vx[i];
vm[i] = 0;
vx[i] = 0;
pold = pcur;
pcur = Power(curm, k2) * curx;
ans += primes[i] * (pcur - pold);
}
for (int d = g << 1; d < maxa; d += g) {
ans -= dp[d];
}
dp[g] = ans;
finans += g * ans;
}
finans *= k;
cout << finans.v << '\n';
return;
}
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
solve(1);
return 0;
}
Setter's solution (PyPy2, PyPy3)
# @author Navneel Singhal
import os
from io import BytesIO
from array import array
input = BytesIO(os.read(0, os.fstat(0).st_size)).readline
def Power(a, n):
ans = 1
while n:
if n & 1:
ans = (ans * a) % 1000000007
a = (a * a) % 1000000007
n >>= 1
return ans
def reducePower(n):
r = n % (1000000007 - 1)
if r == 0 and n != 0:
r = 1000000007 - 1
return r
maxa = int(1e6) + 6
spf, pi, freq, dp, Powerm, Powerx = array('l', [-1] * maxa), array('l', [-1] * maxa), array('l', [0] * maxa), array('l', [0] * maxa), array('l', [0] * maxa), array('l', [0] * maxa)
primes, vm, vx = [], [], []
def main():
picur, pi[0], pi[1] = 0, 0, 0
for i in range(2, maxa):
if spf[i] == -1:
spf[i] = i
picur += 1
primes.append(i)
for j in range(i * i, maxa, i):
if spf[j] == -1:
spf[j] = i
pi[i] = picur
vm, vx = [0] * pi[maxa - 1], [0] * pi[maxa - 1]
n, k, M, X = map(int, input().split())
k2, m, x, finans = reducePower(k - 1), reducePower(M), reducePower(X + M), 0
a = [int(b) for b in input().split()]
for y in a:
freq[y] += 1
for i in range(maxa):
Powerm[i] = (freq[i] * Power(i, m)) % 1000000007
Powerx[i] = (freq[i] * Power(i, x)) % 1000000007
for g in range(maxa - 1, 1, -1):
siz, vgm, vgx, spfg, extra, idx = pi[(maxa - 1) // g], 0, 0, spf[g], False, -1
if pi[spfg] > siz:
if freq[g]:
extra, vgm, vgx = True, Powerm[g], Powerx[g]
else:
if freq[g]:
idx = pi[spfg] - 1
vm[idx], vx[idx] = (vm[idx] + Powerm[g]) % 1000000007, (vx[idx] + Powerx[g]) % 1000000007
r, w = g << 1, 2
while r < maxa:
if freq[r] == 0:
r += g
w += 1
continue
idx = pi[min(spf[w], spfg)] - 1
vm[idx], vx[idx] = (vm[idx] + Powerm[r]) % 1000000007, (vx[idx] + Powerx[r]) % 1000000007
r += g
w += 1
curm, curx, ans, pold, pcur = 0, 0, 0, 0, 0
if extra:
curm, curx, pold = (curm + vgm) % 1000000007, (curx + vgx) % 1000000007, pcur
pcur = (Power(curm, k2) * curx) % 1000000007
ans = (ans + spfg * (pcur - pold)) % 1000000007
for i in range(min(pi[spfg], siz) - 1, -1, -1):
curm, curx = (curm + vm[i]) % 1000000007, (curx + vx[i]) % 1000000007
vm[i], vx[i], pold = 0, 0, pcur
pcur = (Power(curm, k2) * curx) % 1000000007
ans = (ans + primes[i] * (pcur - pold)) % 1000000007
for d in range(g << 1, maxa, g):
ans -= dp[d]
if ans < 0:
ans += 1000000007
dp[g] = ans
finans += g * ans
finans %= 1000000007
idx, siz, w = -1, pi[maxa - 1], 2
while w < maxa:
if freq[w] == 0:
w += 1
continue
idx = pi[spf[w]] - 1
vm[idx], vx[idx] = (vm[idx] + Powerm[w]) % 1000000007, (vx[idx] + Powerx[w]) % 1000000007
w += 1
curm, curx, ans, pold, pcur = 0, 0, 0, 0, 0
for i in range(siz - 1, -1, -1):
curm, curx = (curm + vm[i]) % 1000000007, (curx + vx[i]) % 1000000007
vm[i], vx[i], pold = 0, 0, pcur
pcur = (Power(curm, k2) * curx) % 1000000007
ans = (ans + primes[i] * (pcur - pold)) % 1000000007
for d in range(2, maxa):
ans -= dp[d]
if ans < 0:
ans += 1000000007
finans = ((finans + ans) * (k % 1000000007)) % 1000000007
print(finans)
if __name__ == '__main__':
main()
Setter's solution (Java)
// @author Navneel Singhal
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
PrintWriter out = new PrintWriter(outputStream);
ChefSums solver = new ChefSums();
solver.solve(1, in, out);
out.close();
}
}
class ChefSums {
final int mod = 1000000007;
final int maxa = 1000006;
final int maxpi = 78499;
int[] spf = new int[maxa];
int[] pi = new int[maxa];
int[] freq = new int[maxa];
int[] dp = new int[maxa];
int[] Powm = new int[maxa];
int[] Powx = new int[maxa];
int[] primes = new int[maxpi];
int[] vm = new int[maxpi];
int[] vx = new int[maxpi];
int Power(long a, int n) {
long ans = 1;
while (n > 0) {
if ((n & 1) == 1) {
ans = (ans * a) % mod;
}
a = (a * a) % mod;
n >>= 1;
}
return (int) ans;
}
int min(int a, int b) {
if (a < b) return a;
return b;
}
int reducePower(long P) {
int reducedPower = (int) (P % (mod - 1));
if (reducedPower == 0 && P != 0) {
reducedPower = mod - 1;
}
return reducedPower;
}
void precompute() {
for (int i = 0; i < spf.length; ++i) {
spf[i] = -1;
}
int pi_cur = 0;
pi[0] = pi[1] = 0;
for (int i = 2; i < maxa; i++) {
if (spf[i] == -1) {
spf[i] = i;
primes[pi_cur] = i;
pi_cur++;
if ((long) i * i >= maxa) {
pi[i] = pi_cur;
continue;
}
for (int j = i * i; j < maxa; j += i) {
if (spf[j] == -1) spf[j] = i;
}
}
pi[i] = pi_cur;
}
}
public void solve(int testNumber, InputReader in, PrintWriter out) {
for (int i = 0; i < maxpi; ++i) {
dp[i] = 0;
freq[i] = 0;
vm[i] = 0;
vx[i] = 0;
}
for (int i = maxpi; i < maxa; ++i) {
dp[i] = 0;
freq[i] = 0;
}
precompute();
long k, M, X;
int n, m, x, k2, y, finans = 0;
n = in.nextInt();
k = in.nextLong();
M = in.nextLong();
X = in.nextLong();
k2 = reducePower(k - 1);
m = reducePower(M);
x = reducePower(X + m);
for (int i = 0; i < n; ++i) {
y = in.nextInt();
freq[y]++;
}
for (int i = 0; i < maxa; ++i) {
Powm[i] = (int) (((long) freq[i] * Power((long) i, m)) % mod);
Powx[i] = (int) (((long) freq[i] * Power((long) i, x)) % mod);
if (i >= 7) continue;
}
for (int g = maxa - 1; g > 1; --g) {
int siz = pi[(maxa - 1) / g];
int vgm = 0, vgx = 0;
int spfg = spf[g];
boolean extra = false;
int idx;
if (pi[spfg] > siz) {
if (freq[g] > 0) {
extra = true;
vgm = Powm[g];
vgx = Powx[g];
}
}
else {
if (freq[g] > 0) {
idx = pi[spfg] - 1;
vm[idx] += Powm[g];
if (vm[idx] >= mod) vm[idx] -= mod;
vx[idx] += Powx[g];
if (vx[idx] >= mod) vx[idx] -= mod;
}
}
for (int r = g << 1, w = 2; r < maxa; r += g, ++w) {
if (freq[r] == 0) continue;
idx = pi[min(spf[w], spfg)] - 1;
vm[idx] += Powm[r];
if (vm[idx] >= mod) vm[idx] -= mod;
vx[idx] += Powx[r];
if (vx[idx] >= mod) vx[idx] -= mod;
}
int curm = 0, curx = 0, ans = 0, pold = 0, pcur = 0;
if (extra) {
curm += vgm;
if (curm >= mod) curm -= mod;
curx += vgx;
if (curx >= mod) curx -= mod;
pold = pcur;
pcur = (int) (((long) Power((long) curm, k2) * (long) curx) % mod);
ans += (int) (((long) spfg * (pcur - pold)) % mod);
if (ans < 0) ans += mod;
else if (ans >= mod) ans -= mod;
}
for (int i = min(pi[spfg], siz) - 1; i >= 0; --i) {
curm += vm[i];
if (curm >= mod) curm -= mod;
curx += vx[i];
if (curx >= mod) curx -= mod;
vm[i] = 0;
vx[i] = 0;
pold = pcur;
pcur = (int) (((long) Power((long) curm, k2) * (long) curx) % mod);
ans += (int) (((long) primes[i] * (pcur - pold)) % mod);
if (ans < 0) ans += mod;
else if (ans >= mod) ans -= mod;
}
for (int d = g << 1; d < maxa; d += g) {
ans -= dp[d];
if (ans < 0) ans += mod;
}
// assert(ans >= 0 && ans < mod);
dp[g] = ans;
finans = (int) ((finans + (long) g * (long) ans) % mod);
// assert(finans >= 0 && finans < mod);
}
int idx;
int siz = pi[(maxa - 1)];
assert(siz == maxpi);
for (int w = 2; w < maxa; ++w) {
idx = pi[spf[w]] - 1;
vm[idx] += Powm[w];
if (vm[idx] >= mod) vm[idx] -= mod;
vx[idx] += Powx[w];
if (vx[idx] >= mod) vx[idx] -= mod;
}
int curm = 0, curx = 0, ans = 0, pold = 0, pcur = 0;
for (int i = siz - 1; i >= 0; --i) {
curm += vm[i];
if (curm >= mod) curm -= mod;
curx += vx[i];
if (curx >= mod) curx -= mod;
vm[i] = 0;
vx[i] = 0;
pold = pcur;
pcur = (int) (((long) Power((long) curm, k2) * curx) % mod);
ans += (int) (((long) primes[i] * (pcur - pold)) % mod);
if (ans < 0) ans += mod;
else if (ans >= mod) ans -= mod;
}
for (int d = 2; d < maxa; ++d) {
ans -= dp[d];
if (ans < 0) ans += mod;
}
dp[1] = ans;
finans = (int) ((finans + ans) % mod);
finans = (int) (((long) (k % mod) * finans) % mod);
out.println(finans);
}
}
class InputReader {
public BufferedReader reader;
public StringTokenizer tokenizer;
public InputReader(InputStream stream) {
reader = new BufferedReader(new InputStreamReader(stream), 32768);
tokenizer = null;
}
public String next() {
while (tokenizer == null || !tokenizer.hasMoreTokens()) {
try {
tokenizer = new StringTokenizer(reader.readLine());
} catch (IOException e) {
throw new RuntimeException(e);
}
}
return tokenizer.nextToken();
}
public int nextInt() {
return Integer.parseInt(next());
}
public long nextLong() {
return Long.parseLong(next());
}
}
Setter's solution (Kotlin)
// @author Navneel Singhal
import java.io.*
import java.util.*
fun main(args:Array<String>) {
solve()
}
val mod = 1000000007
val maxa = 1000006
val maxpi = 78499
var spf = IntArray(maxa)
var pi = IntArray(maxa)
var freq = IntArray(maxa)
var dp = IntArray(maxa)
var Powm = IntArray(maxa)
var Powx = IntArray(maxa)
var primes = IntArray(maxpi)
var vm = IntArray(maxpi)
var vx = IntArray(maxpi)
fun Power(aa:Long, nn:Int):Int {
var ans:Long = 1
var n = nn
var a = aa
while (n > 0) {
if ((n and 1) == 1) {
ans = (ans * a) % mod
}
a = (a * a) % mod
n = n shr 1
}
return ans.toInt()
}
fun reducePower(P:Long):Int {
var reducedPower = (P % (mod - 1)).toInt()
if (reducedPower == 0 && P != 0L) {
reducedPower = mod - 1
}
return reducedPower
}
fun precompute() {
for (i in spf.indices) {
spf[i] = -1
}
var pi_cur = 0
pi[1] = 0
pi[0] = pi[1]
for (i in 2 until maxa) {
if (spf[i] == -1) {
spf[i] = i
primes[pi_cur] = i
pi_cur++
if (i.toLong() * i >= maxa) {
pi[i] = pi_cur
continue
}
var j = i * i
while (j < maxa) {
if (spf[j] == -1) spf[j] = i
j += i
}
}
pi[i] = pi_cur
}
}
fun solve() {
for (i in 0 until maxpi) {
freq[i] = 0
vm[i] = 0
vx[i] = 0
}
for (i in maxpi until maxa) {
freq[i] = 0
}
precompute()
var k:Long
var M:Long
var X:Long
var n:Int
var m:Int
var x:Int
var k2:Int
var y:Int
var finans = 0
n = nextInt()
k = nextLong()
M = nextLong()
X = nextLong()
k2 = reducePower(k - 1)
m = reducePower(M)
x = reducePower(X + m)
for (i in 0 until n) {
y = nextInt()
freq[y]++
}
for (i in 0 until maxa) {
Powm[i] = ((freq[i].toLong() * Power(i.toLong(), m)) % mod).toInt()
Powx[i] = ((freq[i].toLong() * Power(i.toLong(), x)) % mod).toInt()
}
for (g in maxa - 1 downTo 2) {
var siz = pi[(maxa - 1) / g]
var vgm = 0
var vgx = 0
var spfg = spf[g]
var extra = false
var idx:Int
if (freq[g] > 0) {
if (pi[spfg] > siz) {
extra = true
vgm = Powm[g]
vgx = Powx[g]
}
else {
idx = pi[spfg] - 1
vm[idx] = (vm[idx] + Powm[g]) % mod
vx[idx] = (vx[idx] + Powx[g]) % mod
}
}
var r = g shl 1
var w = 2
while (r < maxa) {
if (freq[r] == 0) {
r += g
++w
continue
}
idx = pi[minOf(spf[w], spfg)] - 1
vm[idx] = (vm[idx] + Powm[r]) % mod
vx[idx] = (vx[idx] + Powx[r]) % mod
r += g
++w
}
var curm = 0
var curx = 0
var ans = 0
var pold = 0
var pcur = 0
if (extra) {
curm = (curm + vgm) % mod
curx = (curx + vgx) % mod
pold = pcur
pcur = ((Power(curm.toLong(), k2).toLong() * curx.toLong()) % mod).toInt()
ans += ((spfg.toLong() * (pcur - pold)) % mod).toInt()
ans = (ans % mod + mod) % mod
}
for (i in minOf(pi[spfg], siz) - 1 downTo 0) {
curm = (curm + vm[i]) % mod
curx = (curx + vx[i]) % mod
vm[i] = 0
vx[i] = 0
pold = pcur
pcur = ((Power(curm.toLong(), k2).toLong() * curx.toLong()) % mod).toInt()
ans += ((primes[i].toLong() * (pcur - pold)) % mod).toInt()
ans = (ans % mod + mod) % mod
}
var d = g shl 1
while (d < maxa) {
ans = (ans + mod - dp[d]) % mod
d += g
}
dp[g] = ans
finans = ((finans + g.toLong() * ans.toLong()) % mod).toInt()
}
var idx:Int
var siz = pi[(maxa - 1)]
assert((siz == maxpi))
for (w in 2 until maxa) {
idx = pi[spf[w]] - 1
vm[idx] = (vm[idx] + Powm[w]) % mod
vx[idx] = (vx[idx] + Powx[w]) % mod
}
var curm = 0
var curx = 0
var ans = 0
var pold = 0
var pcur = 0
for (i in siz - 1 downTo 0) {
curm = (curm + vm[i]) % mod
curx = (curx + vx[i]) % mod
vm[i] = 0
vx[i] = 0
pold = pcur
pcur = ((Power(curm.toLong(), k2).toLong() * curx) % mod).toInt()
ans += ((primes[i].toLong() * (pcur - pold)) % mod).toInt()
ans = (ans % mod + mod) % mod
}
for (d in 2 until maxa) {
ans = (ans + mod - dp[d]) % mod
}
dp[1] = ans
finans = ((finans + ans) % mod).toInt()
finans = (((k % mod).toLong() * finans) % mod).toInt()
System.out.println(finans)
}
@JvmField val INPUT = System.`in`
@JvmField val OUTPUT = System.out
@JvmField val _reader = INPUT.bufferedReader()
fun readLine(): String? = _reader.readLine()
fun readLn() = _reader.readLine()!!
@JvmField var _tokenizer: StringTokenizer = StringTokenizer("")
fun read(): String {
while (_tokenizer.hasMoreTokens().not()) _tokenizer = StringTokenizer(_reader.readLine() ?: return "", " ")
return _tokenizer.nextToken()
}
fun nextInt() = read().toInt()
fun nextLong() = read().toLong()
@JvmField val _writer = PrintWriter(OUTPUT, false)
inline fun output(block: PrintWriter.() -> Unit) { _writer.apply(block).flush() }
Tester's solution (Kotlin)
package CHEFSUMS
const val MAX_A = 1000003
const val MOD = 1000000007
fun pow (a: Long, b: Long): Long {
if (b > MOD-1) {
val nextB = b % (MOD-1)
return pow(a, if(nextB == 0L) MOD.toLong()-1 else nextB)
}
var x = a
var ret = 1L
var y = b
while (y > 0) {
if (y and 1 == 1L) ret = (ret * x) % MOD
x = (x * x) % MOD
y = y shr 1
}
return ret
}
fun main (args: Array<String>) {
val br = java.io.BufferedReader(java.io.InputStreamReader(System.`in`))
val bw = java.io.BufferedWriter(java.io.OutputStreamWriter(System.`out`))
val smallestPrimeFactor = IntArray(MAX_A+1) { -1 }
val primes = mutableListOf<Int>()
val numPrimesLe = IntArray(MAX_A+3) { 0 }
smallestPrimeFactor[1] = MAX_A + 1
for(p in 2..MAX_A) {
numPrimesLe[p] = numPrimesLe[p-1]
if (smallestPrimeFactor[p] >= 0) {
continue
}
numPrimesLe[p]++
smallestPrimeFactor[p] = p
primes.add(p)
if (p > MAX_A / p) {
continue
}
for (i in p*p .. MAX_A step p) {
if(smallestPrimeFactor[i] == -1) {
smallestPrimeFactor[i] = p
}
}
}
for(i in MAX_A+1..MAX_A+2) numPrimesLe[i] = numPrimesLe[i-1]
val (N, K, M, X) = br.readLine()!!.split(' ').map(String::toLong)
require(N in 1..1000000)
require(K in 1..1000000000000000000L)
require(M in 1..1000000000000000000L)
require(X in 1..1000000000000000000L)
val A = br.readLine()!!.split(' ').map(String::toInt)
require(A.size.toLong() == N)
require(A.all { it in 2..1000000 })
val freq = IntArray(MAX_A+1)
for(v in A) freq[v]++
val `freq_i*i^M` = freq.mapIndexed { i, v -> v * pow(i.toLong(), M) % MOD }
val `freq_i*i^(M+X)` = freq.mapIndexed { i, v -> v * pow(i.toLong(), M+X) % MOD }
val f = LongArray(MAX_A+1)
val `sum^M` = LongArray(MAX_A+2)
val `sum^(M+X)` = LongArray(MAX_A+2)
for (d in MAX_A downTo 1) {
val spfD = smallestPrimeFactor[d]
val sz = numPrimesLe[minOf(MAX_A / d, spfD)]
val jis = (1 .. MAX_A / d).zip((1*d .. MAX_A step d))
for ((j, i) in jis) {
val w = numPrimesLe[minOf(smallestPrimeFactor[j], spfD)] - 1
`sum^M`[minOf(w, sz)] += `freq_i*i^M`[i]
`sum^(M+X)`[minOf(w, sz)] += `freq_i*i^(M+X)`[i]
}
var last = 0L
var `suffix_sum^M` = 0L
var `suffix_sum^(M+X)` = 0L
for (w in sz downTo 0) {
`suffix_sum^M` = (`sum^M`[w] + `suffix_sum^M`) % MOD
`suffix_sum^(M+X)` = (`sum^(M+X)`[w] + `suffix_sum^(M+X)`) % MOD
`sum^M`[w] = 0
`sum^(M+X)`[w] = 0
val cur = pow(`suffix_sum^M`, K-1) * `suffix_sum^(M+X)` % MOD
f[d] += (if(w == sz) spfD else primes[w]) * (cur - last + MOD) % MOD
last = cur
}
for (i in 2*d .. MAX_A step d) f[d] += MOD - f[i]
f[d] = f[d] % MOD
}
val ans = (f.foldIndexed(0L, { index, acc, value -> (acc + index * value) % MOD })) * (K % MOD) % MOD
bw.write("${ans}\n")
bw.flush()
require(br.readLine() == null)
}
Note: after the checkers were updated, the solution that originally ran in ~0.7s now runs in ~0.5s, and thus some suboptimal solutions whose complexity is \mathcal{O}(N \log^2 N) with a small constant factor, with constant optimizations passed in ~0.9s (for example, solutions that sorted the numbers according to spf instead of using the variation of counting sort used above; this works since std::sort is very fast).