Problem :
Pre-Requsite :
The Josephus Problem - Numberphile
Helps a bit with the intution.
Explanation :
Okay so I had a slightly different approach which was not as complicated as the official editorial
So, in the original Josephus problem, you eliminate people until the number of people left is a power of 2. Then that person whose turn it is when there are only 2^k for any k > 0 people remaining is the winner. It’s almost like the circle starts with him and comes back to him.
So after seeing this, I wondered if there can be a similar pattern in this problem. So if you think about it, because Josh never attacks, the soldier to the right of Josh never dies. It’s like he starts the circle and the turn always comes back to him.
I did the same thing as the official editorial describes. Place Josh at all positions and compute the damage he takes at each position in O(log(N)) time. The damage computation part is what is easier.
Algorithm to execute at each position :
For each i, (1 \leq i \leq N) place Josh at position i and kill all the even numbered people between 1 and i (uising 1 index here).
Now starting from soldier i+1 (the soldier to the right of Josh) keep going right and add all the soldiers alive into a new array B. This is an O(N) operaton we will optimize it later. Stop at Josh and do not add him into this array.
Case 1: Even number of soldiers in array B (No Damge)
So if there are even number of soldiers in the array (remember Josh is not included in this array),
1 kills 2
3 kills 4,
…
\text{largest odd} kills \text{largest even}.
So since the soldier before Josh is killed Josh takes no damage. The number of soldiers has reduced to \frac{|B|}{2} . Where, |B| = \text{Number of soldiers in array B}
Case 2: Odd number of soldiers in array B (Some Damage)
So if there are odd number of soldiers in the array,
1 kills 2
3 kills 4
…
\text{2nd largest odd} kills \text{largest even}.
\text{largest odd} damages \text{Josh}.
So now Josh takes damage from the largest odd numbered soldier. The number of soldiers has reduced to \frac{|B|+1}{2}.
This is one single pass over the array. Keep repeating this until there is only 1 soldier left.
Optimization 1 : Using the original Index of B
As you can see you will have to re-index after every pass i.e. after one pass all the odd indices survive, (1,3,5,7,...) So for the next pass we have to re-assgn them to index 1,2,3,4,... respectively. But what if I tell you we can avoid doing that. We can use the indices that were given when B was originally created.
Lets say there are 11 people in our array B originally.
Pass 0 : 1 2 3 4 5 6 7 8 9 10 11 (Initial)
Pass 1 : 1 . 3 . 5 . 7 . 9 .. 11 ( 11 Attacks Josh)
Pass 2 : 1 . . . 5 . . . 9 .. .. ( Nobody Attacks Josh)
Pass 3 : 1 . . . . . . . 9 .. .. ( 9 Attacks Josh)
Pass 4 : 1 . . . . . . . . .. .. ( Nobody Attacks Josh)
So we can get the index of the attacking person with this equation
Basically, we are finding the highest multiple of 2^P that is less than the size of the initial array B.
So combining all of these concepts I implemented this algo and here is my code :
https://www.codechef.com/viewsolution/25262443
This is correct but unable to pass Sub-task 2.
Optimization 2 : Getting rid of B
If you have come so far you have understood the core concept. This part is quite simple. Basically, you will have to map the indicies of the original array B to the array A.
Let bi be the index of the attacking soilder in B
Let ai be the index of the soilder B[bi] in A
All using 1 index
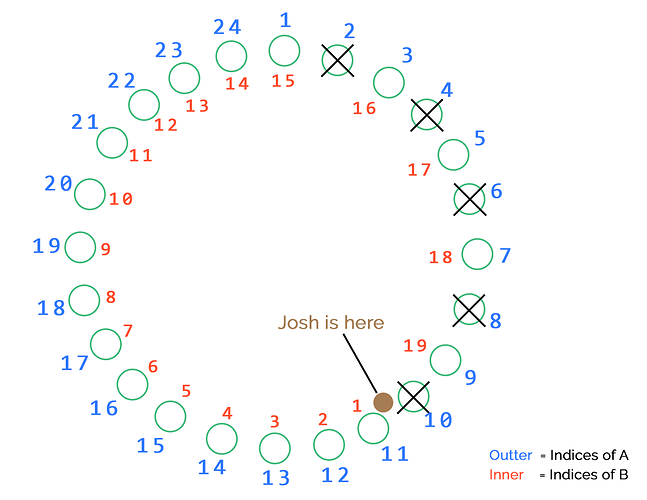
Here is a visualization :
With this we can compute the index of the attacking soldier in B and map that index to an index in A. Please not that here A is the array of all the soldiers without placing Josh anywhere.
Please be aware that I have used 0 indexing in my solution.
Link to Code : CodeChef: Practical coding for everyone
Complexity Analysis :
Time Complexity : O(N * log(N))
SpaceComplexity : O(N)