#PROBLEM LINK:
Author: Tamal Mondal
Tester: Tamal Mondal
Editorialist: Tamal Mondal
#DIFFICULTY:
EASY-MEDIUM
#PREREQUISITES:
Game Theory
#PROBLEM:
In a stack there is N no. of disks. Chef decides how many disks will be there initially and who will make the first move. In each move, a player can remove X (>0) numbers of disks such that X divides K where K in the number of disks present at that time. The player who removes the last disk loses the game. Simply we have to find who will pick up the last disk.
#EXPLANATION:
In each test case who will make the first move and how many disks are there initially, are mentioned. We just have to find the optimal strategy to play this game. It is very easy to find if we create a state diagram having different states. Here a state can be a losing state or a winning state. A state shows how many disks are there in the stack. Definitely state 1 is losing state and if there is a move that leads from the current state to a losing state, the current state is a winning state, and otherwise, the current state is a losing state. In this way, we can classify winning and losing states. See the following diagram.
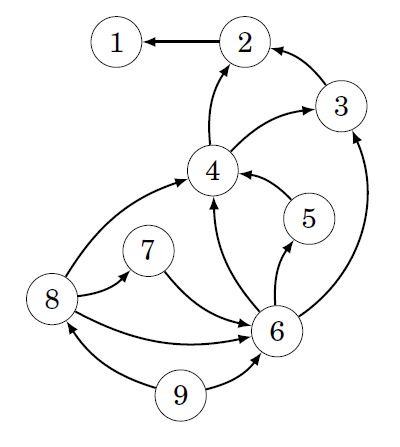
Surprisingly, in this game, all even-numbered states are winning states, and all odd-numbered states are losing states. So if initially no. of disks is even then the player who starts the game will win and if initially, no. of disks is odd then the player who starts the game will lose.
#AUTHOR’S AND EDITORIALIST’S SOLUTIONS:
Author’s and editorialist’s solution can be found here.