Can you prove the time complexity of your solution?
If you prefer a video explanation: CHGORAM Video Solution - February Long Challenge 2020
PROBLEM LINK:
Author: Simon St James
Tester: Radoslav Dimitrov
Editorialist: William Lin
DIFFICULTY:
Medium-Hard
PREREQUISITES:
Trees, Observations, Dynamic Programming
PROBLEM:
We are given a tree and some of the nodes are marked. Find the number of triples of distinct nodes such that all three nodes are marked and all three pairs of nodes within the triple have the same distance.
QUICK EXPLANATION:
For any such triple, there exists a center c such that the distance from c to all three nodes of the triple are equal.
For each node u, count the number triples such that the LCA of the triple is u. There are two cases: when u=c and when u \ne c.
We can calculate dp1_{u,i}, the number of nodes in u's subtree with distance i, and dp2_{u, i}, the number of pairs of nodes (a, b) with the same depth in u's subtree which satisfy (depth(a)-depth(lca(a, b)))-(depth(lca(a, b))-depth(u))=i.
If we process the DP for node u in O(k), where k is the depth of the second deepest subtree of u, then the time complexity is guaranteed to be O(N).
EXPLANATION:
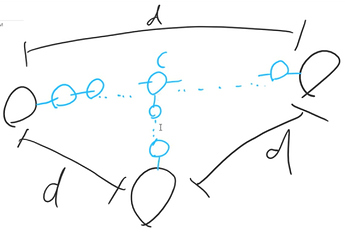
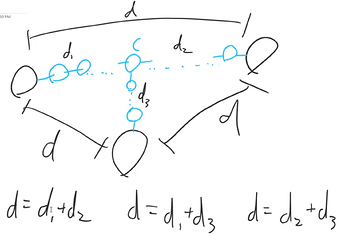
Observation 1. There exists a node c such that c is equidistant to all nodes in the triple.
Proof
On the path between two of the nodes, we know that there is a node c which branches out to the third node:
We can set variables for the distances from c to each of the three nodes and write a system of linear equations:
Solving the system of linear equations shows that c is equidistant to all three nodes.
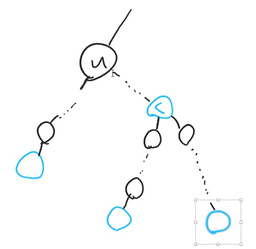
Let’s perform a DFS on the tree, and for each node u that we visit, let’s find the number of triples which have their lowest common ancestor equal to u. For example, this is one such triple:
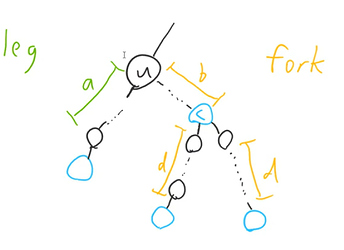
Notice that we can split the component containing the triple into a leg and a fork, as shown below:
Note that in order for a leg to be able to pair with a fork, a=d-b must be satisfied. It seems like if we can somehow find the number of legs and forks coming out of u, we can find the answer for u!
This suggests that we use the following DP: dp1_{u, i} will be the number of legs with a=i which start at node u and dp2_{u, i} will be the number of forks with d-b=i which start at node u.
We need to consider how we can perform the transitions to find dp1_u and dp2_u. The following procedure will be useful for this problem:
- We start with dp1_u and dp2_u representing the single node u.
- Let v_1, v_2, \dots, v_k be the children of u. Let’s merge dp1_{v_1} and dp2_{v_1} to dp1_u and dp2_u somehow, so that 1. the answer will be updated with new triples which form from the union of u and subtree v_1 and 2. dp1_u and dp2_u will represent the union of the node u and the subtree v_1.
- For each i, let’s merge dp1_{v_i} and dp2_{v_i} to dp1_u and dp2_u somehow, so that 1. the answer will be updated with new triples which form from the union of the current processed subtree of u and the subtree v_i and 2. dp1_u and dp2_u will represent the union of the node u and the first i subtrees.
- At the end, dp1_u and dp2_u will represent the entire subtree u.
So now, we need to focus on how we can merge dp1_v and dp2_v with dp1_u and dp2_u.
A. First, because v is deeper than u by 1, we need to change dp1_v and dp2_v. More specifically, all legs from v have a increased by 1, so dp1_{v, j+1}=dp1_{v, j} (and dp1_{v, 0} will be 0), and all forks from v have b increased by 1 and d-b decreased by 1, so dp2_{v, j-1}=dp2_{v, j} (we should just delete dp2_{v, 0} since negative indexes are useless).
B. Next, we need to calculate the triples which form from merging v to u for our total answer. Each triple consists of a leg from v and a fork from u and vice versa. So, for each j, we will add dp1_{v, j}\cdot dp2_{u, j}+dp2_{v, j}\cdot dp1_{u, j} to the total answer.
C. Next, we might have some forks which form from merging v to u. Each fork consists of a leg from v and a leg from u. So, for each j, we will add dp1_{v, j}\cdot dp1_{u, j} to dp2_{u, j}.
D. Lastly, when v becomes part of subtree u, all legs and forks from v should be added to u. So, for each j, we will add dp1_{v, j} to dp1_{u, j} and dp2_{v, j} to dp2_{u, j}.
This DP solution works in O(n^2) time. Let’s try to optimize it.
Let d be the smallest depth of both v_i (the depth including the parent edge) and current processed subtree of u (the union of u with its first i-1 children subtrees).
For step A, let’s view dp1_v and dp2_v both as lists. The transition on dp1_v is equivalent to adding a 0 to the front of the list and the transition on dp2_v is equivalent to removing the first element of the list. These are both linear time operations - unless we store the list in reverse, as operations on the end of the list are constant time. So that’s what we’ll do.
For steps B and C, when we iterate j, we only have to iterate from 0 to d. Why don’t we need to iterate over d? d+1 is greater than the depth of one of the subtrees, so one of dp_{v, d+1} and dp_{u, d+1} is guaranteed to be 0. In steps B and C, all terms are a product dp_{v, d+1} and dp_{u, d+1}, so all j>d will cause these terms to evaluate to 0. This makes steps B and C run in O(d) time.
For step D, if v has the smallest depth, then we don’t need to do anything. Otherwise, we will add dp_u to dp_v instead, and let dp_v replace dp_u. In both cases, we only iterate j up to d, which makes step D run in O(d) time.
In steps B, C, and D, we applied what’s known as the merge-small-to-large on depths - we find the smallest depth d of both subtrees before merging them. Then, we merge the small subtree to the large subtree to take O(d) time for the merge.
Observation 2. The merge-small-to-large trick on depths optimizes the solution to O(n) time.
Proof
Whenever we merge v to u, find the subtree with minimum depth (remember, we consider the parent edge for v, and for u, we only consider the union of u with the first i children subtrees). If both subtrees have the same depth, choose the deepest path with the greatest id for the leaf node. Then, in that subtree, color the deepest path, and if there are multiple, color the one with smallest id for the leaf node. Note that we color O(d) edges, so the total number of edges that we color is the time complexity of our solution.
Below are some examples:
In the example above, subtree u has the minimum depth, so we color the deepest path of u (which is nothing).
In the example above, we merge another child subtree v to u. v has the minimum depth, so we color its deepest path.
In the example above, we finish processing u, and now it becomes a child subtree v to be merged with its parent u. We can see that v has the minimum depth, so we color its deepest path.
We can work with more cases, but it seems like no edge can ever be colored twice!
What can we say about a path when we color it? It’s part of the subtree with minimum depth, so when we merge the two subtrees, that colored path can’t be the deepest path anymore. Since we only color deepest paths, that means we never color a colored path again!
There are O(n) edges in a tree, so if no edge is colored twice, we color at most O(n) edges. Since this is equivalent to the time complexity of our solution, our solution works in O(n) time.
RELATED PROBLEMS:
Merge-small-to-large:
SOLUTIONS:
Setter's Solution
// Simon St James (ssjgz) - Setter's solution for "Equilateral Treeangles" - 2019-07-17.
// Problem was later renamed to "Chef and Gordon Ramsay 2" when I saw CHGORAM in AUG19
// and noticed how my Problem could be turned into a sequel to it :)
#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
#include <cassert>
using namespace std;
const int numTripletPermutations = 1 * 2 * 3; // i.e. == factorial(3).
struct DescendantWithHeightInfo
{
// The number of suitable pairs of descendants of Node with the given height
// that have Node as their Lowest Common Ancestor.
int64_t numPairsWithHeightWithNodeAsLCA = 0;
// The name "number" is not strictly correct: if numPairsWithHeightWithNodeAsLCA > 0, then this
// will indeed be the number of suitable descendants of this Node which have this height,
// but if numPairsWithHeightWithNodeAsLCA == 0, "number" will also be 0.
//
// The "number" count is used to avoid the overcount when performing completeTripletsOfTypeA
// (Centroid Decomposition has no notion of our parent-child relationship, so
// will count "descendants" of a Node alongside "non-descendants" of a Node.)
int number = 0;
};
struct Node
{
vector<Node*> neighbours;
bool isSuitable = false;
int height = 0;
// The total number of entries into descendantWithHeightInfo, summed across *all* nodes,
// will be O(n log n).
map<int, DescendantWithHeightInfo> descendantWithHeightInfo;
};
struct HeightInfo
{
int numWithHeight = 0;
// Make a note of which Node this info has been incorporated into (i.e. which Node's
// descendantWithHeightInfo it has been used to update) so we don't accidentally
// incorporate it into the same Node twice!
Node* lastIncorporatedIntoNode = nullptr;
};
class DistTracker
{
public:
// O(maxDist).
DistTracker(int maxDist)
: m_numWithDist(2 * maxDist + 1),
m_maxDist(maxDist)
{
}
// O(1).
void insertDist(const int newDist)
{
numWithDistValue(newDist)++;
m_largestDist = max(m_largestDist, newDist);
};
// O(1).
int numWithDist(int dist)
{
return numWithDistValue(dist);
}
// O(1).
void adjustAllDists(int distDiff)
{
m_cumulativeDistAdjustment += distDiff;
assert(m_cumulativeDistAdjustment >= 0);
if (m_largestDist != -1)
m_largestDist += distDiff;
}
// O(1).
int largestDist() const
{
return m_largestDist;
}
private:
int m_cumulativeDistAdjustment = 0;
vector<int> m_numWithDist;
int m_maxDist = -1;
int m_largestDist = -1;
int& numWithDistValue(int dist)
{
return m_numWithDist[dist - m_cumulativeDistAdjustment + m_maxDist];
}
};
enum DistTrackerAdjustment {DoNotAdjust, AdjustWithDepth};
template <typename NodeProcessor>
void doDfs(Node* node, Node* parentNode, int depth, DistTracker& distTracker, DistTrackerAdjustment distTrackerAdjustment, NodeProcessor& processNode)
{
if (distTrackerAdjustment == AdjustWithDepth)
distTracker.adjustAllDists(1);
processNode(node, depth, distTracker);
for (auto child : node->neighbours)
{
if (child == parentNode)
continue;
doDfs(child, node, depth + 1, distTracker, distTrackerAdjustment, processNode);
}
if (distTrackerAdjustment == AdjustWithDepth)
distTracker.adjustAllDists(-1);
}
int countDescendants(Node* node, Node* parentNode)
{
auto numDescendants = 1; // Current node.
for (const auto& child : node->neighbours)
{
if (child == parentNode)
continue;
numDescendants += countDescendants(child, node);
}
return numDescendants;
}
int findCentroidAux(Node* currentNode, Node* parentNode, const int totalNodes, Node** centroid)
{
auto numDescendants = 1;
auto childHasTooManyDescendants = false;
for (const auto& child : currentNode->neighbours)
{
if (child == parentNode)
continue;
const auto numChildDescendants = findCentroidAux(child, currentNode, totalNodes, centroid);
if (numChildDescendants > totalNodes / 2)
{
// Not the centroid, but can't break here - must continue processing children.
childHasTooManyDescendants = true;
}
numDescendants += numChildDescendants;
}
if (!childHasTooManyDescendants)
{
// No child has more than totalNodes/2 descendants, but what about the remainder of the graph?
const auto nonChildDescendants = totalNodes - numDescendants;
if (nonChildDescendants <= totalNodes / 2)
{
assert(centroid);
*centroid = currentNode;
}
}
return numDescendants;
}
Node* findCentroid(Node* startNode)
{
const auto totalNumNodes = countDescendants(startNode, nullptr);
Node* centroid = nullptr;
findCentroidAux(startNode, nullptr, totalNumNodes, ¢roid);
assert(centroid);
return centroid;
}
void doCentroidDecomposition(Node* startNode, int64_t& numTriplets)
{
Node* centroid = findCentroid(startNode);
auto addSomeTypeATripletsForNode = [&numTriplets](Node* node, DistTracker& distTracker)
{
// This will be called O(log2 n) times for each node before that node's
// Type A Triplets are fully completed.
for (const auto& heightPair : node->descendantWithHeightInfo)
{
const auto descendantHeight = heightPair.first;
const auto requiredNonDescendantDist = (descendantHeight - node->height);
if (requiredNonDescendantDist > distTracker.largestDist())
break; // Optimisation - no point continuing with larger descendantHeights.
const auto numPairsWithHeightWithNodeAsLCA = heightPair.second.numPairsWithHeightWithNodeAsLCA;
const auto numNewTriplets = numPairsWithHeightWithNodeAsLCA * distTracker.numWithDist(requiredNonDescendantDist) * numTripletPermutations;
assert(numNewTriplets >= 0);
numTriplets += numNewTriplets;
}
};
auto propagateDists = [&addSomeTypeATripletsForNode](Node* node, int depth, DistTracker& distTracker)
{
addSomeTypeATripletsForNode(node, distTracker);
};
auto collectDists = [](Node* node, int depth, DistTracker& distTracker)
{
if (node->isSuitable)
distTracker.insertDist(depth);
};
const auto numNodesInComponent = countDescendants(startNode, nullptr);
{
DistTracker distTracker(numNodesInComponent);
for (auto& child : centroid->neighbours)
{
doDfs(child, centroid, 1, distTracker, AdjustWithDepth, propagateDists );
doDfs(child, centroid, 1, distTracker, DoNotAdjust, collectDists );
}
}
{
DistTracker distTracker(numNodesInComponent);
// Do it again, this time backwards ...
reverse(centroid->neighbours.begin(), centroid->neighbours.end());
// ... and also include the centre, this time.
if (centroid->isSuitable)
distTracker.insertDist(0);
for (auto& child : centroid->neighbours)
{
doDfs(child, centroid, 1, distTracker, AdjustWithDepth, propagateDists );
doDfs(child, centroid, 1, distTracker, DoNotAdjust, collectDists );
}
addSomeTypeATripletsForNode(centroid, distTracker);
}
for (auto& neighbour : centroid->neighbours)
{
assert(std::find(neighbour->neighbours.begin(), neighbour->neighbours.end(), centroid) != neighbour->neighbours.end());
// Erase the edge from the centroid's neighbour to the centroid, essentially "chopping off" each child into its own
// component ...
neighbour->neighbours.erase(std::find(neighbour->neighbours.begin(), neighbour->neighbours.end(), centroid));
// ... and recurse.
doCentroidDecomposition(neighbour, numTriplets);
}
}
void completeTripletsOfTypeACentroidDecomposition(vector<Node>& nodes, Node* rootNode, int64_t& numTriplets)
{
doCentroidDecomposition(rootNode, numTriplets);
// Fix the overcount caused by Centroid Decomposition (over-)counting descendants of a node as non-descendants
// of a node!
for (auto& node : nodes)
{
for (const auto descendantHeightPair : node.descendantWithHeightInfo)
{
const auto height = descendantHeightPair.first;
const auto numPairsWithHeightWithNodeAsLCA = descendantHeightPair.second.numPairsWithHeightWithNodeAsLCA;
// Centroid decomposition would have (wrongly) added numPairsWithHeightWithNodeAsLCA[height] * numTripletPermutations
// for each suitable descendant of node with height "height" - correct for this.
numTriplets -= numPairsWithHeightWithNodeAsLCA * node.descendantWithHeightInfo[height].number * numTripletPermutations;
}
}
}
map<int, HeightInfo> buildDescendantHeightInfo(Node* currentNode, Node* parentNode, int height, int64_t& numTriplets)
{
currentNode->height = height;
map<int, HeightInfo> persistentInfoForDescendantHeight;
for (auto child : currentNode->neighbours)
{
if (child == parentNode)
continue;
// Quick C++ performance note: in C++11 onwards, capturing a returned std::map
// in a local variable is O(1), due to Move Semantics. Prior to this, though,
// it could have been O(size of std::map) (if the Return Value Optimisation ended up
// not being used), which would (silently!) lead to asymptotically worse performance!
//
// Luckily, this code uses C++11 features so we can't accidentally fall into this trap.
auto transientInfoForDescendantHeight = buildDescendantHeightInfo(child, currentNode, height + 1, numTriplets);
if (transientInfoForDescendantHeight.size() > persistentInfoForDescendantHeight.size())
{
// We'll be copying transientInfoForDescendantHeight into persistentInfoForDescendantHeight.
// Ensure that the former is smaller than the latter so that we can make use of the Small-to-Large
// trick. NB: std::swap'ing is O(1).
swap(persistentInfoForDescendantHeight, transientInfoForDescendantHeight);
}
for (auto transientDescendantHeightPair : transientInfoForDescendantHeight)
{
// This block of code (i.e. the body of the containing for... loop)
// is executed O(n log2 n) times over the whole run.
// It is guaranteed to be executed with descendantHeight if the current
// child has a descendant with height descendantHeight that isSuitable and a previous child of this
// node also has a descendant with height descendantHeight that isSuitable, but may also
// be executed under different circumstances.
//
// Since this block of code adds at most one entry into currentNode's descendantWithHeightInfo member,
// the sum of node->descendantWithHeightInfo.size() over all nodes is O(n log2 n).
const auto descendantHeight = transientDescendantHeightPair.first;
const auto& transientHeightInfo = transientDescendantHeightPair.second;
auto& heightInfoForNode = persistentInfoForDescendantHeight[descendantHeight];
assert (descendantHeight > currentNode->height);
auto numUnprocessedDescendantsWithHeight = -1;
auto numKnownDescendantsWithHeight = -1;
assert(transientHeightInfo.lastIncorporatedIntoNode != nullptr);
if (transientHeightInfo.lastIncorporatedIntoNode == currentNode)
{
assert(heightInfoForNode.lastIncorporatedIntoNode != currentNode);
numUnprocessedDescendantsWithHeight = heightInfoForNode.numWithHeight;
numKnownDescendantsWithHeight = transientHeightInfo.numWithHeight;
}
else
{
assert(transientHeightInfo.lastIncorporatedIntoNode != currentNode);
numUnprocessedDescendantsWithHeight = transientHeightInfo.numWithHeight;
numKnownDescendantsWithHeight = heightInfoForNode.numWithHeight;
}
const auto earlierChildHasThisHeight = (numKnownDescendantsWithHeight > 0);
if (earlierChildHasThisHeight)
{
// Incorporate any un-incorporated HeightInfo into this Node's descendantWithHeightInfo.
auto& descendantHeightInfo = currentNode->descendantWithHeightInfo[descendantHeight];
auto& numPairsWithHeightWithNodeAsLCA = descendantHeightInfo.numPairsWithHeightWithNodeAsLCA;
auto& numberDescendantsWithThisHeight = descendantHeightInfo.number;
if (numUnprocessedDescendantsWithHeight * numPairsWithHeightWithNodeAsLCA > 0)
{
// Found a triple where all three nodes have currentNode as their LCA: a "Type B" triple.
const auto numNewTriplets = numPairsWithHeightWithNodeAsLCA * numUnprocessedDescendantsWithHeight * numTripletPermutations;
assert(numNewTriplets >= 0);
numTriplets += numNewTriplets;
}
// These numPairsWithHeightWithNodeAsLCA would, when combined with a non-ancestor of currentNode that isSuitable and is
// (descendantHeight - currentNode->height) distance away from currentNode, form a "Type A" triple.
// We store numPairsWithHeightWithNodeAsLCA for this descendantHeight inside currentNode: the required non-ancestors of
// currentNode will be found by completeTripletsOfTypeA() later on.
numPairsWithHeightWithNodeAsLCA += numUnprocessedDescendantsWithHeight * numKnownDescendantsWithHeight;
if (numberDescendantsWithThisHeight == 0)
{
// This hasn't been updated yet, so has missed the numKnownDescendantsWithHeight; incorporate it now.
numberDescendantsWithThisHeight += numKnownDescendantsWithHeight;
}
numberDescendantsWithThisHeight += numUnprocessedDescendantsWithHeight;
}
// "Copy" the transient info into persistent info, and make a note that this HeightInfo has been incorporated
// into currentNode.
heightInfoForNode.numWithHeight += transientHeightInfo.numWithHeight;
heightInfoForNode.lastIncorporatedIntoNode = currentNode;
}
}
if (currentNode->isSuitable)
{
persistentInfoForDescendantHeight[currentNode->height].numWithHeight++;
persistentInfoForDescendantHeight[currentNode->height].lastIncorporatedIntoNode = currentNode;
}
return persistentInfoForDescendantHeight;
}
int64_t findNumTriplets(vector<Node>& nodes)
{
int64_t numTriplets = 0;
auto rootNode = &(nodes.front());
// Fills in numPairsWithHeightWithNodeAsLCA for each node, and
// additionally counts all "Type B" triples and adds them to results.
buildDescendantHeightInfo(rootNode, nullptr, 0, numTriplets);
// Finishes off the computation of the number of "Type A" triples
// that we began in buildDescendantHeightInfo.
completeTripletsOfTypeACentroidDecomposition(nodes, rootNode, numTriplets);
return numTriplets;
}
template <typename T>
T read()
{
T toRead;
cin >> toRead;
assert(cin);
return toRead;
}
int main(int argc, char* argv[])
{
// This solution is the first one that occurred to me (well, ish - the first one
// didn't use Centroid Decomposition but a technique with similar capabilities
// based around Heavy-Light Decomposition which seems a little faster in practice,
// and was a little simpler for this Problem). Based on the solutions of the Tester
// (and basically everyone who got 100pts on this Problem during the Contest :)),
// it's become clear that this is an unsually clunky and fiddly way of doing things,
// so I'm only going to give a brief overview of it, here - the official Editorial
// solution will doubtless be better to learn from :) This explanation is adapted from
// the "Brief (ha!) Description" that is required when submitting a new Problem Idea.
//
// Anyway, if you're still reading (which you shouldn't be :p), here goes:
//
// Imagine we pick some arbitrary node (I pick node number 1) as the root R of the tree
// and do a DFS from there. Then it can be shown that any triple (p, q, r) will be
// of one of the following two types:
//
//
// Type A - p, q, r have the same lca, from which they are equidistant e.g.
//
// R
// /|\
// ...
// X = lca(p, q, r)
// / | \
// .......
// / | \
// p q r <-- dist(p, x) = dist(q, x) = dist(r, x);
// p, q and r all have same distance from X,
// and so the same distance from R (aka "height").
//
// Type B - the two "lowest" nodes - say q and r wlog, are equidistant from their lca = X.
// p is *not* a descendent of X, but dist(p, X) = dist(q, X) (= dist(r, X)) e.g.
//
// R
// /|\
// ...
// /\
// ... ...
// / \
// p ...
// |
// X = lca(q, r)
// / \
// .......
// / \
// q r <-- dist(p, X) = dist(r, X); p, q have the same distance from R.
//
// Type A is the easiest to compute; Type B is harder and is computed in two phases: the
// first phase is shared with the computation of the number of Type A triplets; the
// second is separate and uses Centroid Decomposition.
//
// There's a reasonably well known algorithm for calculating, for each node v, the set of
// all descendents of v in O(N log N):
//
// findDescendents(root)
// set_of_descendents = empty-set
// for each child c of root:
// set_of_descendents_of_child = findDescendents(c)
// if |set_of_descendents_of_child| > |set_of_descendents|:
// swap set_of_descendents with set_of_descendents_of_child (O(1)).
//
// for each node in set_of_descendents_of_child:
// add node to set_of_descendents
//
// return set_of_descendents
//
// The algorithm looks like it's O(N^2) worst case, but the fact that we always "copy"
// the smaller set into the larger actually makes it asymptotically better (O(N log N)),
// for the same reason as disjoint-union-by-size is O(N log N):
// https://en.wikipedia.org/wiki/Disjoint-set_data_structure#by_size
// I've also seen this technique referred to as the "Small-To-Large Trick".
//
// For a node v, let height(v) = dist(R, v). We adapt the algorithm to compute not the
// set of descendents of each node v, but a count (map) of *heights of descendents of
// suitable nodes of v* i.e. a map where the keys are heights and the values are the
// number of descendents of v which are suitable and have that height; it can be shown
// that this also is achievable in worst case O(N log N).
//
// With some more book-keeping, it can be shown that we can extract, in O(N log N) time
// and space, for all nodes v, for all heights h [NB: obviously such heights are stored
// sparsely, else the space requirements would be O(N^2)]:
//
// the number of pairs of descendents (u', v') of v such that:
// * u' and v' are both suitable;
// * lca(u', v') = v; and
// * height(u') = height(v') = h (and so: dist(u', v) = dist(v', v))
//
// (this is stored as descendantWithHeightInfo.numPairsWithHeightWithNodeAsLCA) and also
//
// the number of triples (u', v', w') of v such that
// * u', v' and w' are all suitable;
// * lca(u', v') = lca(u', w') = lca(v', w') = v; and
// * height(u') = height(v') = height(w') = h (and so:
// dist(u', v) = dist(v', v) = dist(w', v))
//
// This completes Phase one of two.
//
// We see that the latter count of triples is the number of triples of Type A (more
// precisely - it is the number of such triples divided by the number of permutations
// of a triple, 3! - see later).
//
// The former is a step towards the computation of the number of Type B triples -
// referring to the definition of Type B, we've found, for each X, the number of q's
// and r's with a given height h (which equates to a distance d from X: height(q) - height(x))
// and lca X, and now we just need to find for each X and h the number of p's such that
// dist(p, X) = height(q) - height(X). We do this latter step via Centroid Decomposition.
//
// More precisely, Phase one gives us, for each node v, a map from heights to number
// of pairs of descendents called v.numPairsWithHeightWithNodeAsLCA - all in O(N log N)
// time and space.
//
// We then perform Centroid Decomposition with an efficient DistTracker class that
// implements the following API:
//
// * addDistance(newDistance) - adds the distance to the list of tracked distances
// in O(1).
// * addToAllDistances(distanceIncrease) - adds distanceIncrease to each of the
// tracked distances in O(1).
// * getNumWithDistance(distance) - return the number of tracked distances whos
// current value is precisely distance in O(1).
//
// A simple combination of CD and DistTracker allows us to finally "complete" the "q's"
// and "r's" found in Phase one with the "p's" necessary to form a complete, Type B-triplet
// in O(N x (log N) x (log N)).
//
// It can be further shown that if a triplet (p, q, r) of either type A or B is
// counted by the algorithm, then none of its (3! - 1) other permutations - (p, r, q);
// (r, p, q) etc - will be counted, so simply multiplying the count of Type A and
// Type B triplets by 3! gives us the final result.
//
// Well - not quite :) The Centroid Decomposition step doesn't know about parent and
// children in our original DFS from R, so it will overcount triples. For example,
// consider the simple example:
//
// R
// |
// X
// / \
// Y Z
//
// Imagine that Y and Z are the only suitable nodes, so there are no valid triples in
// this example.
//
// Note that X's descendantWithHeightInfo[2].numPairsWithHeightWithNodeAsLCA will be 1.
// The Centroid Decomposition step will then, unfortunately, treat Y as a "completer"
// of this pair (Y, Z) (and will treat Z the same way), resulting in it reporting *2*
// triples, instead of the correct answer of 0. Luckily, it's easy (though clunky) to
// remove this overcount: see DescendantWithHeightInfo::number for more information.
// The proper Editorial solution, and the original HLD-based solution, don't have this
// clunky "overcount correction" step, which is another reason why they are superior :)
//
// The whole algorithm runs in O(N x (log N) x (log N)) time with O(N log N) space.
ios::sync_with_stdio(false);
const auto numTestcases = read<int>();
for (auto t = 0; t < numTestcases; t++)
{
const auto numNodes = read<int>();
assert(1 <= numNodes && numNodes <= 200'000);
vector<Node> nodes(numNodes);
for (auto i = 0; i < numNodes - 1; i++)
{
const auto u = read<int>();
const auto v = read<int>();
assert(1 <= u && u <= numNodes);
assert(1 <= v && v <= numNodes);
nodes[u - 1].neighbours.push_back(&(nodes[v - 1]));
nodes[v - 1].neighbours.push_back(&(nodes[u - 1]));
}
for (auto i = 0; i < numNodes; i++)
{
const auto isSuitable = read<int>();
assert(isSuitable == 0 || isSuitable == 1);
nodes[i].isSuitable = (isSuitable == 1);
}
const auto numTriplets = findNumTriplets(nodes);
cout << numTriplets << endl;
}
assert(cin);
}
Tester's Solution
#include <bits/stdc++.h>
#define endl '\n'
#define SZ(x) ((int)x.size())
#define ALL(V) V.begin(), V.end()
#define L_B lower_bound
#define U_B upper_bound
#define pb push_back
using namespace std;
template<class T, class T1> int chkmin(T &x, const T1 &y) { return x > y ? x = y, 1 : 0; }
template<class T, class T1> int chkmax(T &x, const T1 &y) { return x < y ? x = y, 1 : 0; }
const int MAXN = (1 << 18);
struct mydeque {
vector<int> vec;
int& operator[](const unsigned &pos) { return vec[vec.size() - pos - 1]; }
unsigned size() { return vec.size(); }
void push_front(int x) { vec.pb(x); }
};
void merge(mydeque &a, mydeque &b) {
if(SZ(a) < SZ(b)) swap(a, b);
for(int i = 0; i < SZ(b); i++) {
a[i] += b[i];
}
}
int n, s[MAXN];
vector<int> adj[MAXN];
int read_int();
void read() {
n = read_int();
for(int i = 1; i <= n; i++) {
adj[i].clear();
}
for(int i = 0; i < n - 1; i++) {
int u, v;
u = read_int();
v = read_int();
adj[u].pb(v);
adj[v].pb(u);
}
for(int i = 1; i <= n; i++) {
s[i] = read_int();
}
}
int tr_sz[MAXN], cnt_vers;
bool used[MAXN];
void pre_dfs(int u, int pr)
{
cnt_vers++;
tr_sz[u] = 1;
for(int v: adj[u])
if(!used[v] && v != pr)
{
pre_dfs(v, u);
tr_sz[u] += tr_sz[v];
}
}
int centroid(int u, int pr)
{
for(int v: adj[u])
if(!used[v] && v != pr && tr_sz[v] > cnt_vers / 2)
return centroid(v, u);
return u;
}
int64_t answer = 0;
int dep[MAXN];
int curr_cnt[MAXN], gen_cnt[MAXN];
int64_t cnt[MAXN][2];
void fill_curr_cnt(int u, int pr, int d = 1) {
curr_cnt[d] += s[u];
for(int v: adj[u]) {
if(v != pr && !used[v]) {
fill_curr_cnt(v, u, d + 1);
}
}
}
void dfs1(int u, int pr) {
dep[u] = 0;
for(int v: adj[u]) {
if(v != pr && !used[v]) {
dfs1(v, u);
chkmax(dep[u], dep[v] + 1);
}
}
}
mydeque dp[MAXN];
void add(pair<int, int> &mx, int x) {
if(chkmax(mx.second, x)) {
if(mx.first < mx.second) {
swap(mx.first, mx.second);
}
}
}
int64_t two[MAXN];
int tmp[MAXN];
void dfs2(int u, int pr, int curr_d = 1) {
dp[u].vec.clear();
dp[u].push_front(s[u]);
pair<int, int> mx = {0, 0};
for(int v: adj[u]) {
if(v != pr && !used[v]) {
dfs2(v, u, curr_d + 1);
dp[v].push_front(0);
add(mx, dep[v] + 1);
}
}
int d = mx.second;
for(int i = 0; i <= d; i++) {
tmp[i] = 0;
two[i] = 0;
}
for(int v: adj[u]) {
if(v == pr || used[v]) continue;
int cd = min(d, dep[v] + 1);
for(int i = 1; i <= cd; i++) {
two[i] += tmp[i] * 1ll * dp[v][i];
tmp[i] += dp[v][i];
}
}
for(int i = 1; i <= d; i++) {
int od = i - curr_d;
if(od < 0) continue;
answer += (gen_cnt[od] - curr_cnt[od]) * 1ll * two[i];
}
for(int v: adj[u]) {
if(v != pr && !used[v]) {
merge(dp[u], dp[v]);
}
}
}
void decompose(int u)
{
cnt_vers = 0;
pre_dfs(u, u);
int cen = centroid(u, u);
used[cen] = true;
for(int v: adj[cen])
if(!used[v])
decompose(v);
used[cen] = false;
dfs1(cen, -1);
for(int i = 0; i <= dep[cen] + 1; i++) {
cnt[i][0] = cnt[i][1] = 0;
curr_cnt[i] = 0;
}
fill_curr_cnt(cen, -1, 0);
for(int i = 0; i <= dep[cen] + 1; i++) {
gen_cnt[i] = curr_cnt[i];
curr_cnt[i] = 0;
}
cnt[0][0] = 1;
for(int v: adj[cen]) {
if(!used[v]) {
for(int i = 0; i <= dep[v] + 1; i++) {
curr_cnt[i] = 0;
tmp[i] = 0;
}
fill_curr_cnt(v, cen);
for(int i = 1; i <= dep[v] + 1; i++) {
if(curr_cnt[i]) {
answer += curr_cnt[i] * 1ll * cnt[i][1];
cnt[i][1] += curr_cnt[i] * 1ll * cnt[i][0];
cnt[i][0] += curr_cnt[i];
}
}
dfs2(v, cen);
for(int i = 1; i <= dep[v] + 1; i++) {
curr_cnt[i] = 0;
}
}
}
}
void solve() {
answer = 0;
decompose(1);
cout << answer * 6ll << endl;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int T;
T = read_int();
while(T--) {
read();
solve();
}
return 0;
}
const int maxl = 100000;
char buff[maxl];
int ret_int, pos_buff = 0;
void next_char() { if(++pos_buff == maxl) fread(buff, 1, maxl, stdin), pos_buff = 0; }
int read_int()
{
ret_int = 0;
for(; buff[pos_buff] < '0' || buff[pos_buff] > '9'; next_char());
for(; buff[pos_buff] >= '0' && buff[pos_buff] <= '9'; next_char())
ret_int = ret_int * 10 + buff[pos_buff] - '0';
return ret_int;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mxN=2e5;
int n, s[mxN];
vector<int> adj[mxN];
vector<ll> dp1[mxN], dp2[mxN];
ll ans;
void dfs(int u=0, int p=-1) {
dp1[u]={s[u]};
dp2[u]={0};
for(int v : adj[u]) {
if(v==p)
continue;
dfs(v, u);
//now merge the dp for v to u and update ans
//increase the depths by 1
dp1[v].push_back(0);
dp2[v].pop_back();
//if v is deeper, switch the dp to make it faster
if(dp1[v].size()>dp1[u].size()) {
swap(dp1[u], dp1[v]);
swap(dp2[u], dp2[v]);
}
//make sure dp2[u] is big enough
if(dp2[u].size()<dp1[v].size()) {
//pad dp2[u] with 0s
vector<int> p(dp1[v].size()-dp2[u].size(), 0);
dp2[u].insert(dp2[u].begin(), p.begin(), p.end());
}
//update ans
//leg from v, fork from u
for(int i=1; i<=dp1[v].size(); ++i)
ans+=dp1[v][dp1[v].size()-i]*dp2[u][dp2[u].size()-i];
//fork from v, leg from u
for(int i=1; i<=dp2[v].size(); ++i)
ans+=dp2[v][dp2[v].size()-i]*dp1[u][dp1[u].size()-i];
//combine the dp
//new forks by combining 2 legs
for(int i=1; i<=dp1[v].size(); ++i)
dp2[u][dp2[u].size()-i]+=dp1[u][dp1[u].size()-i]*dp1[v][dp1[v].size()-i];
//just add the rest together
for(int i=1; i<=dp1[v].size(); ++i)
dp1[u][dp1[u].size()-i]+=dp1[v][dp1[v].size()-i];
for(int i=1; i<=dp2[v].size(); ++i)
dp2[u][dp2[u].size()-i]+=dp2[v][dp2[v].size()-i];
}
adj[u].clear();
}
void solve() {
//input
cin >> n;
for(int i=1, u, v; i<n; ++i) {
cin >> u >> v, --u, --v;
adj[u].push_back(v);
adj[v].push_back(u);
}
for(int i=0; i<n; ++i)
cin >> s[i];
//dfs to calculate the answer
ans=0;
dfs();
cout << 6*ans << "\n";
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while(t--)
solve();
}