PROBLEM LINK:
Author: Arjun Arul
Tester: Kevin Atienza
Editorialist: Kevin Atienza
DIFFICULTY:
Medium
PREREQUISITES:
Binary search, bisection method, inversion counting
PROBLEM:
You are given N distinct lines in a plane, and a number K. None of the lines are horizontal or vertical. What is the y-coordinate of the K th intersection from the bottom?
Note that if m lines intersect at a particular point, then that point is counted m(m-1)/2 times. Also, it is guaranteed that there are at least K intersection points.
QUICK EXPLANATION:
The number of intersection points (x,y) with y \le V is the number of pairs of lines whose intercepts in the lines y = V and y = -\infty are in inverted order. For a fixed V, this can be computed in O(N \log N) time using a Fenwick tree or modified merge sort. To find the answer, just binary search the value V to find the lowest one whose number of intersections is \le K.
To get upper and lower bounds for V, you may choose a really large positive number, and a really large negative number. Alternatively, you can try to find the bound dynamically by starting with 1 and doubling until you find an appropriate bound.
EXPLANATION:
Binary search
We want the K th smallest y-coordinate among all intersections of the lines. Many problems involving finding the “K th smallest something” usually can be solved with binary search / bisection method, but for this to be efficient you usually must be able to solve the counting problem counterpart quickly. We’ll describe this in more detail below.
For the current problem, here’s roughly how we can apply the bisection method to solve our problem:
- Let L = -X and R = +X, where X some large positive number.
- While R - L > 10^{-3}, do the following. Let M = \frac{L+R}{2}. Count the number of intersections below the horizontal line y = M. If there are at least K, set R := M, otherwise, set L := M.
- Output R (or L).
The idea here is to maintain a range [L,R] which we’re sure contains the answer, and successively shrink the size of this range by half per step. This proceeds until the range we have is small enough that we already have the answer to the desired precision. The convergence rate of this algorithm is proportional to the precision we want of the answer, which means this will probably take just a few iterations. But for this to actually work, we need to answer the following question quickly:
Given M, count the number of intersections below the horizontal line y = M.
We also need to describe how to select the value X. Roughly, X has to be some value such that all intersections line below the line y = +X and above the line y = -X.
Number of intersections below a horizontal line
Given M, how many intersections are there below the horizontal line y = M?
A naïve way to answer this would be to simply compute all \Theta(N^2) intersections and count those lying below the line. However, this runs in \Theta(N^2) which is very slow, so we must be able to find a way to count them quicker.
Note that every pair of lines intersect at most once. Given a pair of lines L_1 and L_2, when exactly does their intersection lie below y = M (if it exists)? The following image shows some possibilities:
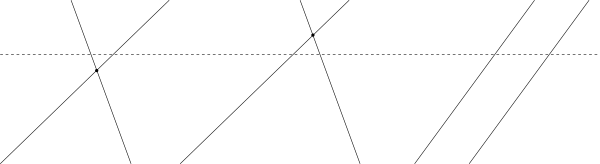
The dashed line represents the line y = M. The first example shows when the intersection lies below the line. The second example shows when it is above. Finally, the third example shows when there is no intersection at all, i.e. the lines are parallel. Note that we didn’t include cases where some lines are horizontal, but luckily such cases are excluded in the problem constraints.
But how do we know when the intersection of L_1 and L_2 lies below? We can imagine it like this. Let P_1 be the intersection of L_1 and y = M, and P_2 be the intersection of L_2 and y = M. Suppose Alice is at P_1 and Bob is at P_2, and then they start walking along the line downwards, while maintaining that their y coordinates are the same. As they walk, the only time that they switch places horizontally is if they pass through the intersection of L_1 and L_2. This means that L_1 and L_2 intersect if and only if Alice and Bob switch places at some point. Now, it can take a very long time before they finally switch places, but we know that they will switch before they reach the line y = -X, due to the way we chose the value X (in the previous section).
This alone doesn’t help much, but there is a much more useful corollary: The number of intersections below y = M is the number of pairs of lines whose intercepts with the lines y = M and y = -X are in different orders relative to each other. In more detail:
- Sort the lines according to the x coordinate of their intersections with y = M. Let’s say the sorted order is L_1, L_2, \ldots, L_N.
- Sort the lines according to the x coordinate of their intersections with y = -X. Let’s say the sorted order is L_{\pi_1}, L_{\pi_2}, \ldots, L_{\pi_N}, where \pi_1, \pi_2 \ldots \pi_N is a permutation of 1, 2 \ldots N.
- Then the number of intersections below the line y = M is simply the number of inversions in the array [\pi_1, \pi_2 \ldots \pi_N]!
This is great, because computing the number of inversions is a standard problem can be done in O(N \log N) time! Also, computing the intersections of each line with a horizontal line can all be done in O(N) time, which means we now have an overall O(N \log N) time to compute the number of intersections below the line y = M!
Choosing X
Finally we must discuss the value X. As mentioned above, X has to be some value such that all intersections line between the lines y = +X and y = -X.
First, we can simply choose X as some fixed, large value that we guess will be large enough for our purposes. While this is the simplest to implement, there are a few drawbacks:
- X has to be really large, because even though the coefficients of the lines are within [-20000,20000], if the lines are very nearly parallel, it’s very possible that the intersection has really large values!
- If X is really large, then the algorithm above might fail if you use floating point values due to rounding errors, so be careful!
It’s also possible to dynamically compute X based on the given input by using successive doubling:
- Start at X = 1.
- Check if all intersections lie between the lines y = +X and y = -X. (using the algorithm above) If so, we stop here, because we already have the desired X.
- Otherwise, double the value of X, i.e. set X := X \cdot 2, and then go back to the previous step.
The advantage is that the X value we choose is guaranteed to be at most twice the minimum possible X value, which means it’s not much larger than necessary. The drawback is that we now have to perform the “inversion count” algorithm above a few more times just for computing X.
Finally, we can simply choose the value X = \infty. However, care must be taken of interpreting the “line” y = -\infty. Strictly speaking, it’s not a line, but we can imagine it as the limit of the line y = -X as X approaches infinity.
Let’s consider what happens to y = -X when X is really, really, really large. What can you say about the order of the intercepts of lines L_1 and L_2 with y = -X? Well, if X is indeed really large, then the line y = -X is so far away from these lines that essentially only the slopes of L_1 and L_2 matter!
This means that if we want to order the lines according to their “intercepts” with the line y = -\infty, we can simply order them according to their slopes (in a certain way: more specifically, in decreasing value of the reciprocals of their slopes).
But there’s another issue with selecting the value X = \infty, namely that we cannot perform the bisection method properly any more. In this case, we can simply find a different value of X that is finite and that we’ll use solely for the upper and lower bounds in our bisection method. Such a value of X can be found for example by “successive doubling” which we discussed earlier.
Time Complexity:
O(B N \log N), where B is the number of iterations in the bisection method