PROBLEM LINKS
DIFFICULTY
HARD
EXPLANATION
Let the matrix P satisfy Pi,j = the probability that Ciel is in j-th node at time 1 if Ciel is in i-th node at time 0. Then, (Pt)i,j is equal to the probability that Ciel is in j-th node at time t if Ciel is in i-th node at time 0.
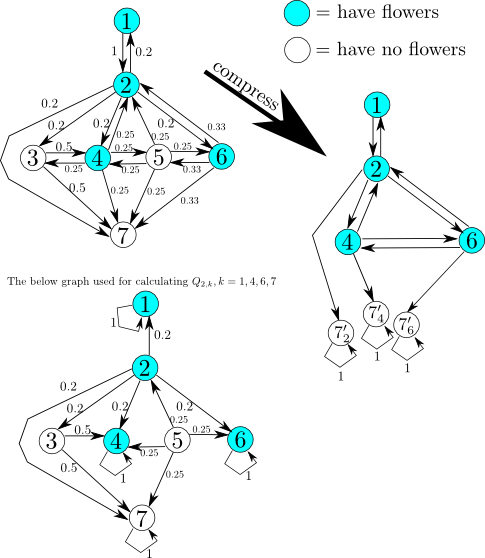
At first, we need to compress the graph as the below figure. The compressed graph contains only the nodes having beautiful flowers, start node, and end node. And the weight of edges Qi,j is the probability that Ciel goes from i-th node to j-th node, without visiting other nodes having beautiful flowers. Qi,j can be calculated as (P∞)i,j, where Pi,j is the weight of the lower left of the below figure. Then we obtain the answers by calculating Q∞ corresponding the right graph of the below graph.
We may calculate PM instead of P∞, where M is an enough large integer. The expectation of the number of Ciel’s move can be around 30! (2108 < 30! < 2109) for some graphs. (Think the graph that the edge from node i to node j exists iff i+1 ≥ j.) Therefore, M must be greater than 30!. For instance, 2110 is enough.
One important thing for calculating PM is thinking about a numerical error. The sums of Pi,k for all k should be 1. But in the computer, this may be slight different from 1.
Therefore, the elements of PM will be 0 or inf. To avoid this trouble, a normalization is needed, that is, the sums of probabilities should be keep 1.
The total complexity for this algorithm is O(N4*log N!).
Note that P∞ may be calculated by solving linear equations with Gaussian elimination. However, because Gaussian elimination is not good algorithm in terms of a numerical error, this method may get WrongAnswer. If a bignum arithmetic is used, this method also can be accepted.
SETTER’S SOLUTION
Can be found here.
TESTER’S SOLUTION
Can be found here.