PROBLEM LINK:
Setter: Rami
Tester: Teja Vardhan Reddy
Editorialist: Taranpreet Singh
DIFFICULTY:
Easy
PREREQUISITES:
Geometry, Trigonometry.
PROBLEM:
Given two circles P1 with centre A(x1, y1) and radius r1 and P2 with centre B(x2, y2) and radius r2. Determine whether there exists a point P which lies inside, or at border of P1, but strictly outside P2, and find such point.
EXPLANATION
By definition of circle, we want to find a point P such that distance between P and A(x1, y1) is less than or equal to r1 and distance from B(x2, y2) is greater than r2.
Thus, we need to point within first circle, which is farthest from centre of second circle. We can see, if that point lies within second circle, first circle lies within second circle, and there doesn’t exist any such point. Let’s call this best point.
We can see, that since the best point need to be as far as possible from B, it’s best to move directly in opposite direction starting from A till we reach the permieter of circle P1. Let’s Call this point C(x3, y3).
People say a picture is worth 1000 words, so, attaching one. ![]()
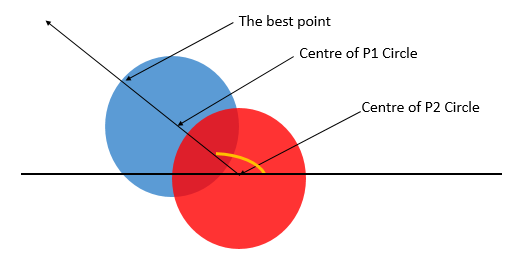
Proof this point is optimal, is below.
Suppose point D(x4, y4) is the optimal point, which is not same as C and lies on perimeter. We can see, that a non-degenerate triangle formed by points A, point B and point D. Using triangle inequality, we can see that dist(D, B) < dist(D, A)+dist(A, B). But for point C, we have dist(C, B) = dist(C, A)+dist(A, B) which proves that point C is more distant from B than any other point D.
Now, let’s calculate point C. We know, it lies on line formed by points A and B. So, we can find the slope as well as equation of line using two point form. We also have equation of first circle, solving them gives us this point (and one other point, we need to be careful). But there’s a simpler way.
Let’s consider θ being the angle formed by line AB as shown by yellow arc in image. Consider a right triangle whose base and perpendicular are parallel to x-axis and y-axis respectively and whose hypotenuse is AC. Length of AC is r1. It can be seen, that we can find the length of base and perpendicular using trigonometry (base is r1*cos(θ) and perpendicular is r1*sin(θ)). This allows us to calculate coordinates of C.
Final check, if the distance between B and C is strictly greater than r2, C is our required point, otherwise no such point exists.
If the centres of both circles coincide, It is easy to see, that answer exists, if r1 > r2 and any point C can also be easily calculated.
Bonus:
Is there any simpler method, if we were to answer only YES/NO and not the point (without calculating the point)?
There may be many related problems, try using geometry tag on problems at SPOJ, Codeforces.
TIME COMPLEXITY
Time complexity is O(1) per test case.
SOLUTIONS:
Tester's Solution
//teja349
#include <bits/stdc++.h>
#include <vector>
#include <set>
#include <map>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <climits>
#include <utility>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <iomanip>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
//setbase - cout << setbase (16); cout << 100 << endl; Prints 64
//setfill - cout << setfill ('x') << setw (5); cout << 77 << endl; prints xxx77
//setprecision - cout << setprecision (14) << f << endl; Prints x.xxxx
//cout.precision(x) cout<<fixed<<val; // prints x digits after decimal in val
using namespace std;
using namespace __gnu_pbds;
#define f(i,a,b) for(i=a;i<b;i++)
#define rep(i,n) f(i,0,n)
#define fd(i,a,b) for(i=a;i>=b;i--)
#define pb push_back
#define mp make_pair
#define vi vector< int >
#define vl vector< ll >
#define ss second
#define ff first
#define ll long long
#define pii pair< int,int >
#define pll pair< ll,ll >
#define sz(a) a.size()
#define inf (1000*1000*1000+5)
#define all(a) a.begin(),a.end()
#define tri pair<int,pii>
#define vii vector<pii>
#define vll vector<pll>
#define viii vector<tri>
#define mod (1000*1000*1000+7)
#define pqueue priority_queue< int >
#define pdqueue priority_queue< int,vi ,greater< int > >
#define flush fflush(stdout)
#define primeDEN 727999983
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
// find_by_order() // order_of_key
typedef tree<
int,
null_type,
less<int>,
rb_tree_tag,
tree_order_statistics_node_update>
ordered_set;
#define int ll
main(){
std::ios::sync_with_stdio(false); cin.tie(NULL);
int t;
cin>>t;
while(t--){
int x1,y1,x2,y2,r1,r2;
cin>>x1>>y1>>r1>>x2>>y2>>r2;
int dist2=(x2-x1)*(x2-x1)+(y2-y1)*(y2-y1);
if(r1>r2 || (dist2>(r2-r1)*(r2-r1))){
cout<<"YES"<<endl;
}
else{
cout<<"NO"<<endl;
continue;
}
long double dist=sqrt((double)dist2);
if(dist2==0){
cout<<x1+r1<<" "<<y1<<endl;
}
else{
cout<<setprecision(30)<<(x1*(dist+r1)-r1*x2)/dist;
cout<<" ";
cout<<setprecision(30)<<(y1*(dist+r1)-r1*y2)/dist<<endl;
}
}
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
import java.text.*;
class CIRCLES2{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
double x1 = nd(), y1 = nd(), r1 = nd(), x2 = nd(), y2 = nd(), r2 = nd();
if(x1 == x2){
if(y1 == y2){
//Same centres
if(r1 <= r2)pn("NO");
else {
//Any point on perimeter of first circle is valid
pn("YES");
print(x1+r1, y1);
}
}else{
if(y1 < y2){
if(y1-r1 < y2-r2){
pn("YES");
print(x1, y1-r1);
}else pn("NO");
}else{
if(y1+r1 > y2+r2){
pn("YES");
print(x1, y1+r1);
}else pn("NO");
}
}
}else{
double theta = Math.atan2(y2-y1, x2-x1);
double x3 = x1-r1*Math.cos(theta), y3 = y1-r1*Math.sin(theta);
if(dist(x3, y3, x2, y2) - r2 > eps){
pn("YES");
print(x3, y3);
}else pn("NO");
}
}
double dist(double x1, double y1, double x2, double y2){
return Math.sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
void print(double x, double y){
pn(df.format(x)+" "+df.format(y));
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
DecimalFormat df = new DecimalFormat("0.00000000000");
static boolean multipleTC = true;
double eps = 1e-7;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new CIRCLES2().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to Share your approach, if you want to. (even if its same ![]() ) . Suggestions are welcomed as always had been.
) . Suggestions are welcomed as always had been. ![]()