PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Vitaly Demidenko
Tester & Editorialist: Taranpreet Singh
DIFFICULTY
Medium-Hard
PREREQUISITES
Union-disjoint sets, Euler Tour and Fenwick Tree
PROBLEM
You are given a tree with N vertices (numbered 1 through N).
A simple path between two different vertices a and b (a \lt b) is called a clamp path if it does not contain any vertices with numbers smaller than a or greater than b.
Calculate the number of clamp paths in the given tree.
QUICK EXPLANATION
- From the given two trees, build two rooted trees T_1 and T_2
- T_1 is constructed such that if node u is an ancestor of node v, then the path from node u to node v doesn’t have any node with a value smaller than u
- T_2 is constructed such that if node u is an ancestor of node v, then the path from node u to node v doesn’t have any node with a value greater than u
- The problem reduces to counting the number of pairs (u, v) such that node u is an ancestor of node v in T_1 and node v is an ancestor of node u in T_2, which can be done by doing Euler tour over T_1 tree and then performing DFS on T_2.
- T_1 (and T_2) can be constructed by processing the nodes in descending (ascending) order of values, and maintaining the disjoint set union, making the new node the parent of roots reachable from the current node.
EXPLANATION
Let’s consider counting the number of pairs (a, b) such that path from a to b does not contains a node with value smaller than a. For this, we shall build a rooted tree where node u is ancestor of node v if and only if on path from node u to node v, there is no node with value smaller than u
Construction of Rooted Tree
Let’s start with all the nodes being marked as inactive and considering the nodes in descending order of value one by one.
The set of active nodes make a forest. Let’s maintain an invariant that each component is maintained as a rooted tree, where root of the tree is the node with smallest value.
Let’s see how we can maintain the same invariant while adding the next node u. This node must have value smaller than existing nodes. So, we just need to consider all components reachable from node u, find their roots (say node v), and make node u the parent of node v. For this, we can maintain disjoint set union maintaining the connected components, and iterate over active neighbours of node u and finding their roots.
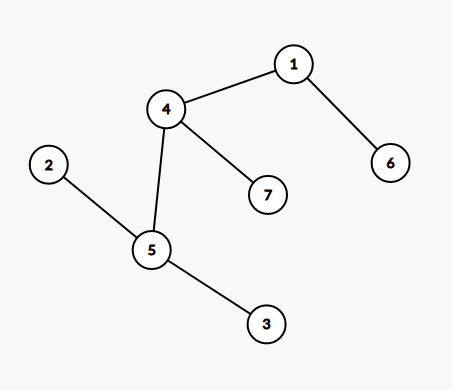
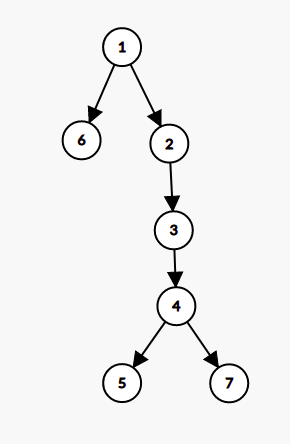
First image denotes the tree given in problem sample. Second image denotes the tree generated when considering nodes in descending order. For example, We can see that from node 3, we can reach node 4, node 5 and node 7 while visiting node with value \geq 3, but we cannot visit nodes 1, node 2 and node 6
Construction Steps
This text will be hidden
The construction first considered nodes 7, node 6 and then node 5 in this order, and added no edges. Then node 4 is processed and directed edges are added to node 5 and node 7. Node 3 is processed and edge to root of component containing node 4, which is node 4 itself, so edge is added from 3 to 4 and 3 becomes root of component. Then edge 2 to 3 is added when processing node 2, node 2 is root. Finally, node 1 is processed and directed edges are added from 1 to 2 and 1 to 6.
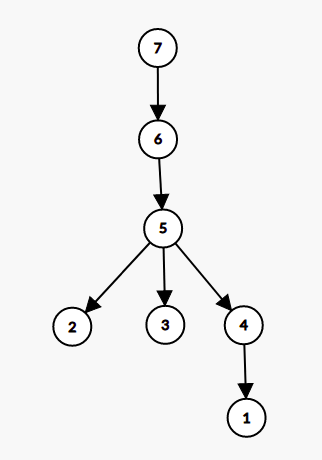
Similarly, we can construct a tree T_2, where node u is ancestor of node v if and only if simple path from node u to node v doesn’t contain any node with value greater than u. Following image depict this tree generated for sample.
Reduction
With these two trees, can we rewrite the condition of clamp paths? yes, we can.
A pair (u, v) forms a clamp path, if and only if node u is ancestor of node v in T_1, and node v is ancestor of node u in T_2.
Reduced Problem and Implementation
Given two rooted trees T_1 and T_2, find the number of pairs (u, v) such that u is ancestor of v in T_1 and v is ancestor of node u in T_2.
Rewriting conditions, Node v is in subtree of node u in T_1 and node v is ancestor of node u in T_2. We shall try all u, and try to count the number of valid v for each u.
Let’s do a DFS on T_2, adding node u to a special structure when we enter node u, and removing node u from the structure when DFS exit the node u. This way, when DFS reaches node u, all nodes present in our structure shall be ancestors of node u.
So we need to count the number of nodes present in our structure, which are in subtree of node u in T_1. When concerned with subtree queries on tree, Euler Tour of Tree is the natural choice.
Our structure must support following operation
- Add a node into structure
- Remove a node from structure
- Count the number of nodes present in structure, which are in subtree of node x in T_1
So, Let’s do Euler tour on T_1, storing the enter and exit times T_{in} and T_{out}. Whenever we add a node u, we mark the position T_{in}(u) with 1, and when we remove node u, we mark the position T_{in} with 0. So the number of nodes in subtree of node x is the number of ones in range T_{in}(x) and T_{out}(x).
These operations are easily supported by fenwick tree of segment tree, though fenwick tree is faster, therefore recommended, since the TL of this problem was tight.
Alternate interpretation of reduced problem
Let’s find euler order in both trees, and let’s draw on plane where one axis is t_{in} in the first tree (let’s call it t1_v), and the other axis is t_{in} in the second tree (t2_v). Locus of points (t1_u, t2_v) such that v is fixed and ancestor of u in the first tree is a horizontal segment, locus of points (t1_u, t2_v) such that u is fixed and ancestor of v in the second tree is a vertical segment. Pair (v, u) is good if these segments intersect.
Now the problem is “given N horizontal and N vertical segments on a plane, calculate the number of intersections”. It is solvable in O(N*log(N)) via scanline with Fenwick tree.
Why Centroid Decomposition approaches got TLE?
There also exist a seemingly very promising solution using centroid decomposition, which consider each path from u to v as the concatenation of two path u to C to v, and make pairs (mn_1, mx_1) and (mn_2, mx_2) for paths u to C and path C to v such that a path is a clamp, if and only if mn_1 \leq mn_2 and mx_1 \leq mx_2 holds. This subproblem can be solved offline using sorting and fenwick tree.
The time complexity of this approach is O(N*log^2(N)) which we intended to TLE, which is why N = 2^{20} = 1048576 was chosen, quite high for a O(N*log^2(N)) \sim 4*10^8 operations, with some constant factor.
TIME COMPLEXITY
The time complexity is O(N*log(N))
SOLUTIONS
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
auto operator<<(ostream&o,const auto&v)->enable_if_t<!is_constructible_v<string,decltype(v)>,decltype(o<<*end(v))>{int f=0,u=&o==&cerr&&o<<"[";for(auto&&x:v)(f++?o<<(u?", ":" "):o)<<x;return u?o<<"]":o;}
auto operator<<(ostream&o,const auto&t)->enable_if_t<__is_tuple_like<decltype(t)>::value,ostream&>{o<<"<";apply([&o](auto&...x){int f=0;(((f++?o<<", ":o)<<x),...);},t);return o<<">";}
#ifdef BIZON
#define rr(...) [](const auto&...x){ cerr << boolalpha << "\e[1;38;5;68m" << #__VA_ARGS__ << " "; int f=0; ((cerr<<"\e[0;38;5;61m"<<",="[!f++]<<"\e[0m "<<x),...)<<endl; }(__VA_ARGS__);
#else
#define rr(...) 0;
#define endl '\n'
#endif
#define ALL(c) begin(c), end(c)
#define II(T, ...) T __VA_ARGS__; [](auto&...x){(cin>>...>>x);}(__VA_ARGS__);
#define ii(...) II(int, __VA_ARGS__)
inline bool umin(auto&x, const auto&y){ return y<x && (x=y, 1); }
inline bool umax(auto&x, const auto&y){ return y>x && (x=y, 1); }
using ll = int64_t;
template<typename T>
struct rsq {
rsq(size_t sz = 0): f(sz) {}
rsq(const vector<auto> &vals): f(size(vals)) {
for(auto i = size(vals); i--;) {
f[i]+=vals[i];
if(auto j = i&(i+1); j) f[j-1]+=f[i];
}
}
T sum_suf(size_t i) const {
T s = T();
for(;i<size(f);i|=i+1) s+=f[i];
return s;
}
T operator()(size_t l, size_t r) const {
if(l>=r) return T();
return sum_suf(l) - sum_suf(r);
}
void add(size_t i, const T &val) {
for(++i; i; i&=i+1) f[--i]+=val;
}
private: vector<T> f;
};
struct dsu {
dsu(size_t n = 0): sz(n,1), p(n) {
iota(begin(p),end(p),0);
}
size_t get(size_t i){
size_t v = i;
while(v!=p[v]) v = p[v];
while(i!=p[i]) i = exchange(p[i],v);
return v;
}
bool unite(size_t i, size_t j){
i = get(i);
j = get(j);
if(i==j) return false;
if(sz[i]<sz[j]) swap(i,j);
p[j] = i;
sz[i]+=sz[j];
return true;
}
size_t size(size_t i){
return sz[get(i)];
}
private:
vector<size_t> p, sz;
};
template<typename ...T>
struct graph {
using E = conditional_t<sizeof...(T), tuple<size_t,T...>, size_t>;
graph(size_t n = 0): g(n) {}
void add_dir_edge(size_t from, size_t to, const T&... args) {
assert(from<size() && to<size());
g[from].emplace_back(to, args...);
}
void add_edge(size_t x, size_t y, const T&... args) {
add_dir_edge(x, y, args...);
add_dir_edge(y, x, args...);
}
const vector<E>& operator[](size_t i) const { return g[i]; }
size_t size() const { return g.size(); }
private: vector<vector<E>> g;
};
auto tree_stuff(const auto &g, size_t root) {
size_t n = size(g), tn = 0;
vector<size_t> par(n,-1), tin(n), tout(n);
function<void(size_t)> go = [&](size_t v) {
tin[v] = tn++;
for(size_t i : g[v]) if(i!=par[v]) {
par[i] = v;
go(i);
}
tout[v] = tn;
};
go(root);
return tuple(tin, tout);
}
int main(){
if(auto f="in.txt"; fopen(f,"r") && freopen(f,"r",stdin));
cin.tie(0)->sync_with_stdio(0);
ii(n)
graph g(n);
for(int i=0;i<n;++i) {
ii(j)
if(j--) g.add_edge(i, j);
}
auto make_tree = [&](auto cmp) {
graph t(n);
dsu u(n);
vector<int> root(n), ids(n);
iota(ALL(ids),0); sort(ALL(ids),cmp);
for(int x : ids) {
for(int i : g[x]) if(cmp(i,x)) {
int y = root[u.get(i)];
t.add_dir_edge(x, y);
u.unite(x, i);
}
root[u.get(x)] = x;
}
return t;
};
auto g1 = make_tree(std::less<int>{});
auto g2 = make_tree(std::greater<int>{});
auto [t1in, t1out] = tree_stuff(g1,n-1);
auto [t2in, t2out] = tree_stuff(g2,0);
vector<pair<int,pair<int,int>>> segs;
vector<pair<int,pair<int,int>>> points;
for(int i=0;i<n;++i) {
segs.emplace_back(t2in[i], pair(t1in[i],t1out[i]));
points.emplace_back(t2in[i], pair(t1in[i], +1));
points.emplace_back(t2out[i], pair(t1in[i], -1));
}
sort(ALL(segs));
sort(ALL(points));
ll ans = -n;
rsq<int> f(n);
auto it = begin(points);
for(auto [y,seg] : segs) {
while(it!=end(points) && it->first <= y) {
auto [x, a] = it->second;
f.add(x, a);
++it;
}
ans+=f(seg.first, seg.second);
}
cout<<ans<<endl;
return 0;
}
Tester's Solution
import java.util.*;
import java.io.*;
class CLAMPWAY{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni();
int[] P = new int[N];
for(int i = 0; i< N; i++)P[i] = ni()-1;
int[][] g = graph(N, P, true);
int[] par1 = new int[N], par2 = new int[N];
Arrays.fill(par1, -1);
Arrays.fill(par2, -1);
int[] order = java.util.stream.IntStream.range(0, N).toArray();
{
int[] set = java.util.stream.IntStream.range(0, N).toArray();
for(int x:order){
for(int v:g[x]){
if(v < x){
int y = find(set, v);
par1[y] = x;
set[y] = x;
}
}
}
}
for(int i = 0, j = N-1; i< j; i++, j--){
int tmp = order[i];
order[i] = order[j];
order[j] = tmp;
}
{
int[] set = java.util.stream.IntStream.range(0, N).toArray();
for(int x:order){
for(int v:g[x]){
if(v > x){
int y = find(set, v);
par2[y] = x;
set[y] = x;
}
}
}
}
int[][] T1 = graph(N, par1, false);
int[][] T2 = graph(N, par2, false);
int R1 = N-1, R2 = 0;
FenwickTree ft = new FenwickTree(N);
int[] st = new int[N], en = new int[N];
euler(T1, st, en, R1);
pn(dfs(T2, ft, st, en, R2));
}
long dfs(int[][] tree, FenwickTree ft, int[] st, int[] en, int u){
long ans = ft.sum(st[u], en[u]);
ft.add(st[u], 1);
for(int v:tree[u])ans += dfs(tree, ft, st, en, v);
ft.add(st[u], -1);
return ans;
}
void euler(int[][] tree, int[] st, int[] en, int u){
st[u] = ++time;
for(int v:tree[u])euler(tree, st, en, v);
en[u] = time;
}
int time = -1;
int find(int[] set, int u){return set[u] = (set[u] == u?u:find(set, set[u]));}
int[][] graph(int N, int[] P, boolean undirected){
int[] cnt = new int[N];
for(int i = 0; i< N; i++){
if(P[i] == -1)continue;
cnt[P[i]]++;
if(undirected)cnt[i]++;
}
int[][] g = new int[N][];
for(int i = 0; i< N; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< N; i++){
if(P[i] == -1)continue;
g[P[i]][--cnt[P[i]]] = i;
if(undirected)g[i][--cnt[i]] = P[i];
}
return g;
}
class FenwickTree {
long[] bit;
int N;
//uses 0-based indexing
public FenwickTree(int N){
this.N = N;
bit = new long[N];
}
void add(int idx, long delta){
for (; idx < N; idx = idx | (idx + 1))
bit[idx] += delta;
}
long sum(int r){
int ret = 0;
for (; r >= 0; r = (r & (r + 1)) - 1)
ret += bit[r];
return ret;
}
long sum(int l, int r){return sum(r)-sum(l-1);}
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = false;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new Thread(null, new Runnable() {public void run(){try{new CLAMPWAY().run();}catch(Exception e){e.printStackTrace();System.exit(1);}}}, "1", 1 << 28).start();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()