PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3
Author: Daanish Mahajan
Tester: Rahul Dugar
Editorialist: Nandini Kapoor
DIFFICULTY:
Easy
PREREQUISITES:
Graph, BFS/Level Order Traversal, Multiset
(Alternatively Dijkstra’s Shortest Path Algorithm)
PROBLEM:
Chef’s college is starting next week. There are S subjects in total represented using an array A, and he needs to choose K of them to attend each day, to fulfill the required number of credits to pass the semester. There are N+1 buildings. His hostel is in building number 0. Subject i is taught in building S[i]. After each subject, there is a break, during which he goes back to his hostel. There are M bidirectional paths of size 1 which connects building u to building v. Find the minimum possible total distance Chef needs to travel each day if he chooses his subjects wisely.
Note that further in the editorial, the term level of a node x with respect to a fixed node in a graph has been used to describe the number of edges in the smallest path from the fixed node to node x.
QUICK EXPLANATION:
As the hostel and other buildings form a graph with unit weights of all paths, we only need to know the levels of this graph in which each of the considered buildings lie (considered buildings being the ones teaching one of the subjects from 1 to S inclusive).
Considering the hostel to be the lone source at level 0, the one way journey to any building will be x units from the hostel, where x represents the level in which the target building lies. Selecting the K subjects which have the nearest buildings assigned to their teaching will result in the minimum possible distance Chef needs to travel.
EXPLANATION:
The college has been given to have a hostel building and N remaining buildings where subjects are taught. Which of these buildings are connected by paths of 1 unit length is also given. This data given can be represented as a graph with buildings as nodes and paths as edges. Since all the paths are of unit length, the weight of each edge will be assigned as 1. An implication of unit long paths is that the distance traveled from the hostel to building B will be equal to the level of B with respect to the hostel in the graph.
Proof
Consider the hostel (node 0) to be at level 0, all nodes that can be reached from node 0 by means of a single edge are at level 1 with respect to node 0. Similarly any building reachable from the hostel by means of x bidirectional paths each connecting a unique pair of buildings will be at level x with respect to the hostel.
We establish the relation between the number of edges e (needed to be crossed from hostel to reach any other building) and level L (of a building with respect to the hostel):
e=L
If we need to travel from 0 to x in this graph and e number of edges E_1 to E_{e} constitute the path from 0 to x, then the total distance D of our path will be given by:
D = \sum_{i=1}^{e} d(E_i)
where d(E_i) represents the length of edge E_i. In this case, the lengths of individual paths are given to be 1 each, thus we obtain:
D = \sum_{i=1}^{e} 1
D = e
which from the earlier established relation can be written as:
D = L
Where L is the level of node x with respect to node 0.
As the graph is not acyclic, a single node x can have multiple ways of reaching from 0 through different sets of edges. It may seem to belong to different levels due to this, in this case we will consider that it belongs to the smallest of these levels (closest one to level 0) because we are required to find the minimum distance traveled by Chef implying if more than a single path exist to a node from 0 we shall follow the smallest weighted one.
Example
If there exist 2 paths from node 0 to x consisting of e and f edges respectively (e\lt f). Let the paths be constituted by edges E_1 to E_{e} and F_1 to F_{f} respectively. In such a case, our level L of node x with respect to node 0 will be e enabling us to have smaller path covered from hostel to building x by Chef.
In case e = f, both paths will result in the same level of x, thus no conflict arises.
To implement this assignment of levels to nodes, we can use breadth first traversal (level order traversal) of the graph we have converted the input into. More about this algorithm can be found here and here.
Starting the level order traversal from node 0 and level 0, as we encounter that one whole level has been popped out of the queue and their children (the next level) have been pushed into it, we increment the level and continue the traversal.
Once all the buildings in which 1 to S subjects are taught have been given a level with respect to the hostel, we need to select K from among these such that they hold the minimum levels. The buildings can appear more than once i.e. there can exist cases whereby more than 1 subject is being taught in a single building, thus while selecting the K buildings with minimum levels we need to make sure the same building can be selected as many times as the number of different subjects being taught in it.
To establish this we utilize a multiset. Traverse all buildings in which 1 to S subjects are being taught and insert their corresponding levels into a multiset. The sum of first K elements of this multiset will give us the distance traveled by Chef from the hostel to those buildings in which the subjects he chose are being taught, thus we multiply this by 2 to obtain the final answer (as he returns to his hostel after each subject, thus needing to travel the same distance he had to while coming from hostel to the building).
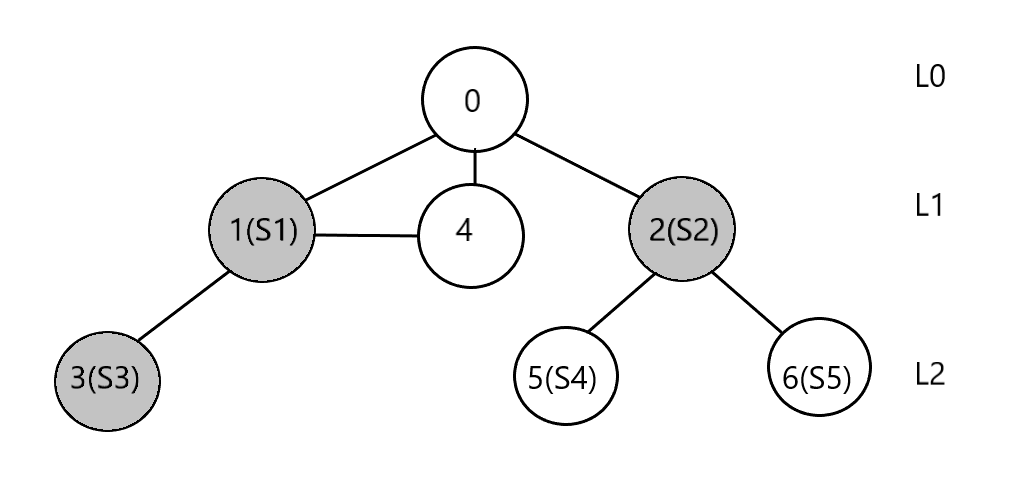
The sample input provided with the problem statement would have a graph as represented below:
6 7 5 3
0 1
0 2
0 4
1 3
1 4
2 5
2 6
1 2 3 5 6
Where L_i represents the i_{th} level, S_i represents the i_{th} subject, and the numbers written in the nodes represent the building numbers, 0 being the hostel. The colored nodes are selected for obtaining minimum traveled distance.
Alternatively, the buildings 5 or 6 could also have been chosen instead of 3, i.e. subject S4 or S5 instead of S3 would also have given the minimum distance (8 in this case). This is because all the alternatives suggested lie in the same level as the selected node and thus if selected in place of the selected node will not hinder the minimum distance.
TIME COMPLEXITY:
O(max(N, log(S)\times S)) per test case.
Because the level order traversal takes O(N) time and the multiset construction takes O(log(S)\times S) i.e. S insert operations of O(s_i) each, for all s_i from 0 to S-1.
Complexities for operations on used containers can be found - for multiset and for queue.
SOLUTIONS:
Setter
#include <bits/stdc++.h>
#define pb push_back
#define ll long long int
#define pii pair<int, int>
using namespace std;
const int maxn = 1e5;
const int maxm = 2e5;
const int maxs = 1e5;
const int maxt = 6;
int main()
{
int t; cin >> t;
while(t--){
int n, m, s, k; cin >> n >> m >> s >> k;
vector<int>g[n + 1];
for(int i = 0; i <= n; i++)g[i].clear();
int u, v;
for(int i = 0; i < m; i++){
cin >> u >> v;
assert(u != v);
g[u].pb(v); g[v].pb(u);
}
int a[n + 1], d[n + 1];
bool visit[n + 1];
memset(a, 0, sizeof(a)); memset(d, 0, sizeof(d)); memset(visit, false, sizeof(visit));
int now = 0, end = 0; d[0] = 0; a[0] = 0; visit[0] = true;
while(now <= end){
for(int v : g[a[now]]){
if(visit[v])continue;
a[++end] = v; d[v] = d[a[now]] + 1;
visit[v] = true;
}
++now;
}
multiset<int> mset; mset.clear();
int id;
for(int i = 0; i < s; i++){
cin >> id;
mset.insert(d[id]);
}
ll ans = 0;
for(auto it = mset.begin(); it != mset.end() && --k >= 0; it++){
ans += *it;
}
ans = 2 * ans;
cout << ans << endl;
}
}
Tester
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#ifndef rd
#define trace(...)
#define endl '\n'
#endif
#define pb push_back
#define fi first
#define se second
#define int long long
typedef long long ll;
typedef double f80;
typedef pair<int, int> pii;
typedef pair<double, double> pdd;
#define double long double
#define pll pair<ll,ll>
#define sz(x) ((long long)x.size())
#define fr(a,b,c) for(int a=b; a<=c; a++)
#define rep(a,b,c) for(int a=b; a<c; a++)
#define trav(a,x) for(auto &a:x)
#define all(con) con.begin(),con.end()
const int infi=0x3f3f3f3f;
const ll infl=0x3f3f3f3f3f3f3f3fLL;
const int mod=998244353;
//const int mod=1000000007;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update> oset;
auto clk=clock();
mt19937_64 rang(chrono::high_resolution_clock::now().time_since_epoch().count());
int rng(int lim) {
uniform_int_distribution<int> uid(0,lim-1);
return uid(rang);
}
int powm(int a, int b) {
int res=1;
while(b>0) {
if(b&1)
res=(res*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return res;
}
long long readInt(long long l,long long r,char endd){
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true){
char g=getchar();
if(g=='-'){
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g && g<='9'){
x*=10;
x+=g-'0';
if(cnt==0){
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd){
if(is_neg){
x= -x;
}
assert(l<=x && x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l,int r,char endd){
string ret="";
int cnt=0;
while(true){
char g=getchar();
assert(g!=-1);
if(g==endd){
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt && cnt<=r);
return ret;
}
long long readIntSp(long long l,long long r){
return readInt(l,r,' ');
}
long long readIntLn(long long l,long long r){
return readInt(l,r,'\n');
}
string readStringLn(int l,int r){
return readString(l,r,'\n');
}
string readStringSp(int l,int r){
return readString(l,r,' ');
}
vi gra[100005];
int dist[100005];
int A[100005];
int cnt[100005];
void solve() {
int n=readIntSp(1,100000),m=readIntSp(1,200000),s=readIntSp(1,100000),k=readIntLn(1,s);
fr(i,0,n) {
gra[i].clear();
cnt[i]=0;
dist[i]=-1;
}
dist[0]=0;
fr(i,1,m) {
int u=readIntSp(0,n),v=readIntLn(0,n);
assert(u!=v);
gra[u].pb(v);
gra[v].pb(u);
}
fr(i,1,s) {
if(i!=s)
A[i]=readIntSp(1,n);
else
A[i]=readIntLn(1,n);
cnt[A[i]]++;
}
queue<int> bfs;
vi order;
bfs.push(0);
while(bfs.size()) {
int at=bfs.front();
order.pb(at);
bfs.pop();
for(int j:gra[at])
if(!(~dist[j])) {
dist[j]=dist[at]+1;
bfs.push(j);
}
}
fr(i,1,n)
assert(~dist[i]);
int ans=0;
for(int i=1; k; i++) {
int te=min(cnt[order[i]],k);
k-=te;
ans+=2*te*dist[order[i]];
}
cout<<ans<<endl;
}
signed main() {
ios_base::sync_with_stdio(0),cin.tie(0);
srand(chrono::high_resolution_clock::now().time_since_epoch().count());
cout<<fixed<<setprecision(1);
int t=readIntLn(1,3);
// cin>>t;
fr(i,1,t)
solve();
assert(getchar()==EOF);
#ifdef rd
cerr<<endl<<endl<<endl<<"Time Elapsed: "<<((double)(clock()-clk))/CLOCKS_PER_SEC<<endl;
#endif
}
Editorialist
#include<bits/stdc++.h>
using namespace std;
#define _z ios_base::sync_with_stdio(false); cin.tie(NULL);
#define int long long int
#define endl "\n"
#define mod 1000000007
#define pb_ push_back
#define mp_ make_pair
//____z___
int n, m, s, k;
void bfs(vector<int> paths[], int vis[], int level[]) {
queue<int>q;
int lev=0;
q.push(0);
q.push(-1);
while(q.size()!=1) {
if(q.front()==-1) {
lev++;
q.pop();
q.push(-1);
continue;
}
int curr=q.front();
q.pop();
level[curr]=lev;
for(int i=0; i<paths[curr].size(); i++) {
if(vis[paths[curr][i]]==0) {
q.push(paths[curr][i]);
vis[paths[curr][i]]=1;
}
}
}
}
void solve()
{
cin>>n>>m>>s>>k;
vector<int> paths[n+1];
int vis[n+1]={1}, dist=0;
for(int i=0; i<m; i++) {
int u, v;
cin>>u>>v;
paths[u].pb_(v);
paths[v].pb_(u);
}
int sub[s], level[n+1]={0};
for(int i=0; i<s; i++) cin>>sub[i];
bfs(paths, vis, level);
multiset<int>ans;
for(int i=0; i<s; i++) {
ans.insert(level[sub[i]]);
}
auto it=ans.begin();
for(int i=0; i<k; i++) {
dist+=*it;
it++;
}
cout<<dist*2<<endl;
}
int32_t main()
{
_z;
int t=1;
cin>>t;
while(t--)
{
solve();
}
}