PROBLEM LINK
Author and Editorialist: Soumik Sarkar
Tester: Avijit Agarwal
DIFFICULTY
Easy-Medium… or so we thought.
PREREQUISITES
Some maths, geometry
PROBLEM
A ball moves in an n-dimensional space with fixed velocity. Given starting position of both ball and Chef, find the minimum velocity required by Chef to intercept the ball before it leaves a given region.
EXPLANATION
Using a straight path is better than a curved path. Using a fixed speed is better than changing speeds. So it is always optimal for Chef to move with constant velocity (speed and direction) starting at t = 0 until he meets the ball at some point.
First, if the position of Chef and the ball already coincide, output should be 0.
If not, we proceed to calculate t_{exit}, the time when the ball moves out of Chef’s court. This is can be done by iterating over each dimension i and checking when the ball moves out the bounds (0 or l_i) of this dimension. The minimum over all dimensions gives t_{exit}.
Beyond this, there can be multiple solutions for this problem. Tester’s solution is easier and requires a bit of geometry and the right perspective. Author’s solution is more analytical and does not require geometry.
Tester’s solution
The problem has only three points of interest: the ball’s position at t = 0, Chef’s position at t = 0, and the ball’s position at t = t_{exit}. So, these points can transferred to a plane where their relative positions are preserved, reducing the problem from n dimensions to 2 dimensions.
Let us denote the ball’s initial position as A, Chef’s initial position as B and the ball’s position at t_{exit} as C. The ball’s velocity is v and Chef’s is u.
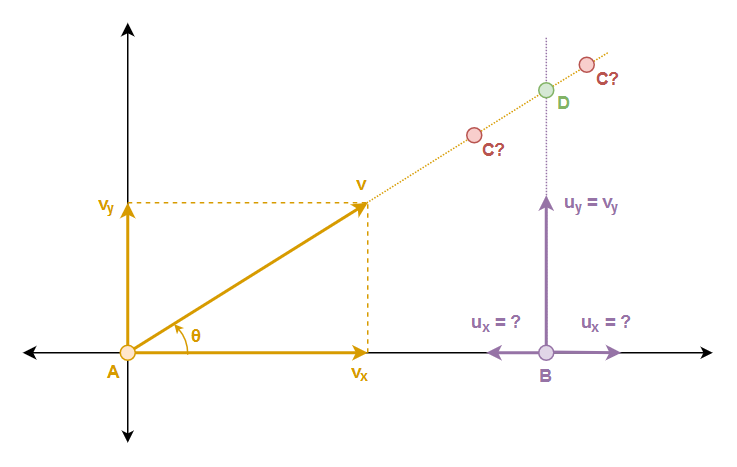
Consider the illustration above. When placed as such with both A and B on the X-axis, it is clear that in order to meet sometime at t > 0 it is necessary that u_y = v_y. But what value of u_x should be chosen? Any value in (-\infty, v_x) will allow them to meet eventually. But to minimize the speed, of course we should choose u_x = 0. Thus Chef’s minimum speed is given by v_y = v \sin \theta.
But, this is the answer only when the point D is encountered by the ball before C since the ball has left the court after position C. If C appears before D, Chef must meet the ball at C instead.
A third case arises when the ball is not moving towards Chef, which means v_x \le 0. In this case too, it can be shown that it is best to meet the ball at the exit point C.
Author’s solution
Consider each dimension separately. In the dimension i, the position of the ball after time t is given by b_i + v_i \cdot t. Let the component of Chef’s chosen velocity along dimesnion i be u_i. Then, if Chef’s position coincides with the ball at time t,
Speed of Chef is given by the magnitude of Chef’s velocity, which is
Here p, r > 0. So, Chef’s required speed can be expressed as a function of time. This function gives a curve for t \ge 0 which is monotonic decreasing when q \ge 0 and unimodal with a single minima for q < 0. So, ternary search can be applied to find the minima in the range [0, t_{exit}]. Alternately, the derivative of the function can also be analyzed to get the minima, which is at -2 \frac{p}{q}.
You can play with the function on Desmos.
Time complexity is \mathcal{O}(n) using geometric approach or getting minima of the cost function directly. Using ternary search it is \mathcal{O}(n + \log \frac{t_{exit}}{ \varepsilon}) where \varepsilon is the desired precision in time (around 10^{-8} will work) and t_{exit} \le 50.
AUTHOR’S AND TESTER’S SOLUTIONS
Author’s solution can be found here
Tester’s solution can be found here.
