PROBLEM LINK
Author and Editorialist: Soumik Sarkar
Tester: Sarthak Manna
DIFFICULTY
Medium-hard
PREREQUISITES
Dynamic programming, centroid decomposition
PROBLEM
Given a tree with n vertices and 3 values x, y, z find the number of ordered triplets i, j, k such that \text{dist}(i, j) = x, \text{dist}(j, k) = y and \text{dist}(i, k) = z.
EXPLANATION
Assume without loss of generality x \le y \le z.
Any triplet can be in one of 2 forms:
All 3 vertices are on one path, this happens when x + y = z.

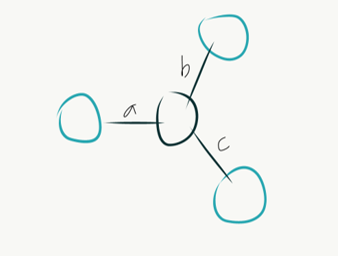
All 3 vertices must form a Y shape, this happens when x + y > z.
For x + y < z, neither of those is the case and the answer is 0.
Let us focus on the Y case, the path case can easily be handled later.
If the triplet forms a Y, the length of each arm is denoted by a, b, c. Clearly, x, y, z are a + b, b + c, a + c. It is trivial to obtain a, b, c from x, y, z. Note that this is impossible when x + y + z is odd, so in this case too the answer is 0.
Let us call the meeting point of the 3 arms as the center of the triplet. Every triplet has exactly one center. We will attempt count the number of triplets that have vertex i as center for all i and sum them up to get the total.
Consider vertex i as root. Let us denote by \text{cnt}_a(i, j) the number of vertices at distance a from i in the subtree of the j^{th} child of i. Similarly define \text{cnt}_b(i, j) and \text{cnt}_c(i, j). To form a triplet with i at the center, we must take 3 vertices at distances a, b, and c from 3 different subtrees. If we take a vertex at distance a from subtree j_1, a vertex at distance b from subtree j_2 and a vertex at distance c from subtree j_3, then the number of ways to do this is \text{cnt}_a(i, j_1) \cdot \text{cnt}_b(i, j_2) \cdot \text{cnt}_c(i, j_3). We require the sum of these products over all pairwise distinct j_1, j_2, j_3 to get the total count. This can be computed by dynamic programming.
Let f(j, mask) be the number of ways to select vertices from the first j subtrees where mask denotes which of a, b, c are required can be represent by an integer from 0 to 7.
Pseudocode for recursive evaluation:
f(j, mask):
if j == 0:
return 1 if mask == 0 else 0
res = f(j - 1, mask)
if bit 0 set in mask:
res += f(j - 1, mask with 0th bit off) * cnt_a(i, j)
if bit 1 set in mask:
res += f(j - 1, mask with 1st bit off) * cnt_b(i, j)
if bit 2 set in mask:
res += f(j - 1, mask with 2nd bit off) * cnt_c(i, j)
return res
The number of triplets with center at i is calculated as f(number of children of i, 7).
Now consider the case when all 3 vertices are on a path. This is a special case where a, b > 0 and c = 0. In this case we need to count the number of ways to take vertices at distances a and b from two different subtrees. The third vertex at distance 0 is i itself. So the number of triplets is f(number of children of i, 3).
This gives us an \mathcal{O}(n^2) solution. We can run a dfs/bfs from each vertex i and calculate all \text{cnt} values beforehand.
To pass the time limit, we need a more efficient approach to precompute these values. This is where centroid decomposition comes in. Centroid decomposition applies the technique of divide and conquer on trees. To learn more refer here and here.
For implementation details, refer to the author’s solution.
A global array dist_cnt is maintained and dist_cnt[x] stores how many vertices are at distance x from the current centroid.
At each step of the divide and conquer, we find a centroid and update its \text{cnt} values with a dfs into its children.
Then we populate dist_cnt and dfs into each subtree one by one such that dist_cnt contains only counts from other subtrees.
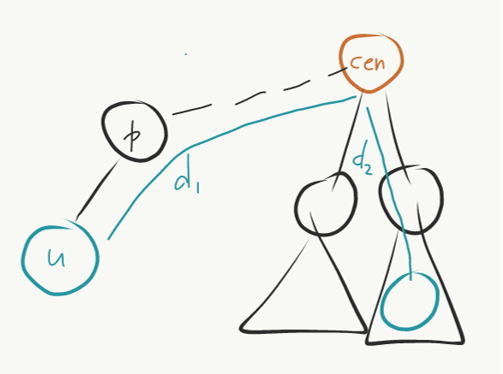
As shown in the image above, checking the index of d_2 in the global array will give the number of vertices at distance d_1 + d_2 from the current vertex. These vertices lie beyond the centroid in other subtrees. In this way we obtain the number of vertices at distances a, b, c which would be in the subtree of p if u is made the root.
Complexity of this solution is \mathcal{O}(n \log^2 n). Centroid decomposition takes \mathcal{O}(n \log n) however for each node one binary search is required to locate the index of the neighbour which connects it to the centroid. Alternately, one may use a map for this purpose.
AUTHOR’S AND TESTER’S SOLUTIONS
Author’s solution can be found here
Tester’s solution can be found here.