PROBLEM LINK:
Author: Erfan Alimohammadi
Tester: Hussain
Editorialist: Oleksandr Kulkov
DIFFICULTY:
MEDIUM-HARD
PREREQUISITES:
Sweep line, segment tree or BIT
PROBLEM:
You’re given N \leq 300 points on 2D-plane in general position. You have to calculate number of subsets of points such that their convex hull is quadrilateral modulo 10^9+7.
QUICK EXPLANATION:
Calculate for each triangle on points (i,j,k) how many points lie strictly inside it, let this value be d_{ijk}. Then iterate over all pairs of points (i,j) and point k lying above segment (i,j). You should add 2^{d_{ijk}} \times \sum\limits_{l\text{ is below }(i,j) \\ ikjl\text{ is convex}}2^{d_{ijl}} to the answer and divide the answer by 2 in the end (because each subset was counted with both diagonals of its convex hull).
EXPLANATION:
Let’s fix vertices of convex hull \{A,B,C,D\}. How many subsets are there with such convex hull?
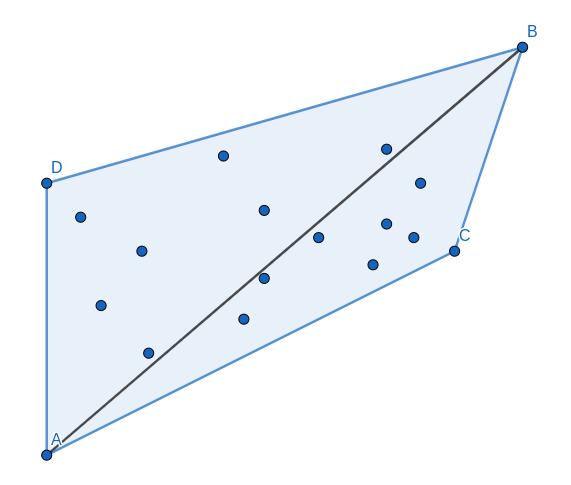
In each such subset you must take all points \{A,B,C,D\} and you may bring any subset of inner points (including \varnothing) as well, but no outer points. Since all points are in general position, you don’t have to bother about points lying on edges of hull or on diagonal AB. Thus let \sharp ABCD be the number of points inside polygon \square ABCD, then the number of subsets having \{A,B,C,D\} as vertices of convex hull is exactly 2^{\sharp ABCD} = 2^{\sharp ABC + \sharp ABD} = 2^{\sharp ABC} \times 2^{\sharp ABD}.
Now that we splitted subset generation on two independent triangles \triangle ABC and \triangle ABD, we may efficiently enumerate all subsets having AB as diagonal in convex hull.
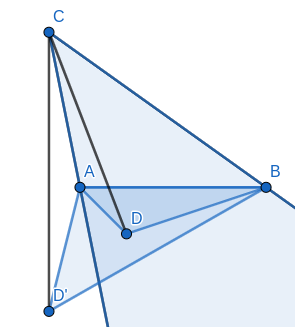
Let’s fix segment AB and iterate over point C. What are points D which we may use to complement \triangle ABC to convex quadrilateral \square ABCD? As you may see, those are points such that segment CD intersects segment AB. If you fix ordering by angle around A and B it would mean that possible positions for D with fixed C will form continuous segments in both orderings.
Formally let’s introduce relation X <_A Y which means (X-A) \times (Y-A)<0 where A\times B stands for pseudo scalar product of vectors A and B. Informally it means that X lies to the left (counter-clockwise) from Y if you look at them from point A. We may sort all points by polar angle around point A using this comparator. Note that you also must take into consideration which half-plane points lie in, since sorting order is determined up to a cyclic shift. Code for comparator:
int plane(point r) {
return r.y() < 0 || r.y() == 0 && r.x() < 0;
}
bool leq(point a, point x, point y) {
x -= a, y -= a;
if(plane(x) == plane(y)) {
return cross(x, y) < 0;
} else {
return plane(x) < plane(y);
}
}
We may compute all orderings around all points in O(n^2 \log n) in advance. Now let’s consider sorting around A for both points above AB (possible C) and below it (possible D). When you go for next possible point C you’ll have to add some possible points D into consideration, which is determined by \angle CAD < 180^\circ. Among those points you have to sum up 2^{\sharp ABD} but only if condition \angle CBD < 180^\circ is met.
And if first condition was met automatically because we implement it in ordering around A, to cut out points not satisfying second condition we should utilize some data structures. Namely, condition \angle CBD < 180^\circ for fixed C will form some contiguous segment of possible points D in ordering around B. Thus we may consider segment tree (or even BIT) over this ordering where initially each cell has value 0 but when we add new point D according to ordering around A, we should add 2^{\sharp ABD} in corresponding cell and update answer with the following value:
Note that when calculating segment thresholds, it will actually be segment in circular array, thus for thresholds l\leq r you have to sum up for D \in [l,r] and for l>r you sum up on [l,n] and [1,r].
After this is done each subset is actually counted twice: for AB and for CD thus you will have to halve the number you obtained to get the answer. This part works in O(n^3 \log n) given that we calculated all possible \sharp ABC, but how to calculate them?
You may utilize the same idea as for calculating area of triangle here.
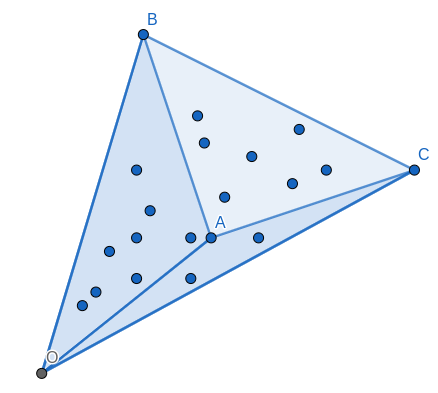
If you want to calculate \sharp ABC, you may actually split it as:
\sharp ABC = \sharp OBC - \sharp OBA - \sharp OAC-1
For arbitrary point O, given that there are no points on segments OA, AB and AC which would be the case if you take O from the given set of points since no three points may lie on same line. In this way you may simply fix some point O, then iterate over all possible triples (A,B,C) and add 1 to \sharp OBC if A \in \triangle OBC which may be checked in O(1), thus the whole working time for calculating \sharp OBC for all pairs (B,C) will be O(n^3) which concludes the whole O(n^3 \log n) solution.
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.