Problem Statement Ravi is given an array A of N integers. He recently has studied the concept of Arithmetic Mean at his school, and now he wishes to apply it to the Array. Now, his dad as always, comes up with a tricky question for him. Ravi is asked, what is the minimum integer that should be added to the array, so that the Arithmetic Mean of all the elements 1 become at least two times the initial Arithmetic Mean. Write a program to help Ravi solve this question. Note: Print the ceil value if there is decimal value. Its getting passed for test case: 1 2 3 4 5
whose average is 3 so i need 6 so i would add 21 and this is the code
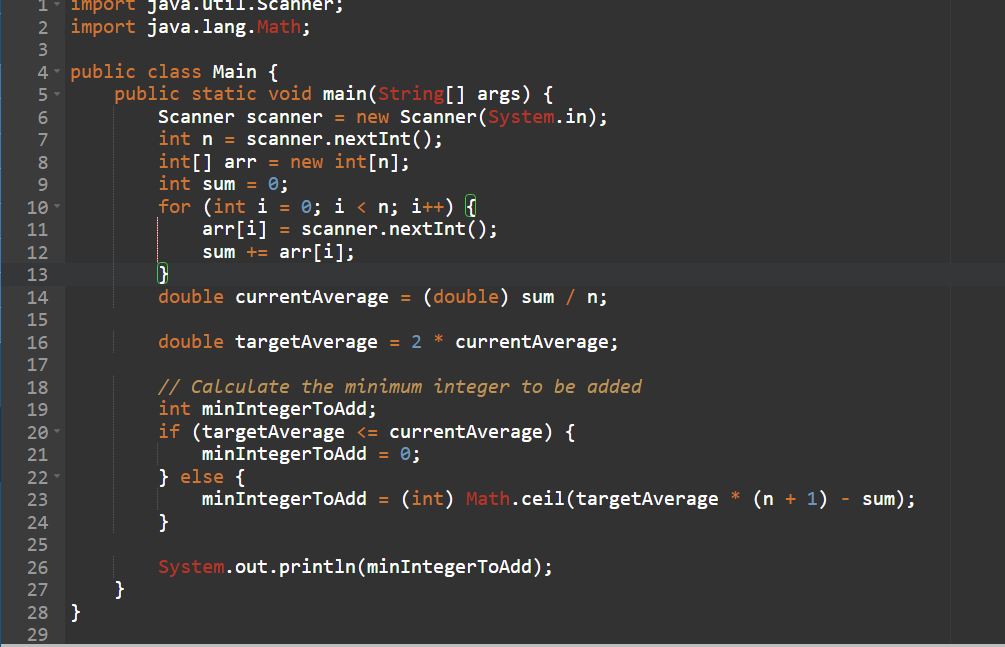
Sorry pasting the screenshot
1 Like
Welcome @jabish144!
Math-wise, your solution appears right.
minIntegerToAdd = (int) Math.ceil(targetAverage * (n + 1) - sum);
Putting in algebra terms, if n is the number of integers in the array, and S is the sum of those integers, the mean m of the array is \frac{S}{n}. We seek the smallest x so that when we append it to the original array, the new mean \frac{S+x}{n+1} is at least 2m.
Following the algebra:
\ \ \frac{S+x}{n+1} \ge 2 \frac{S}{n}
…which means…
\ \ x \ge 2 \frac{S }{n} (n + 1) - S
In your code, targetaverage is 2 \frac{S}{n}, so it looks correct.
Could you please post a link to the online problem statement and your code? What’s the problem?
Scott