Codenation Republic Hiring challenge

1

How many of you guys had given the codenation hiring contest?
How many questions you have got AC?

1 Like
2

I gave a try and got 2 AC. First and third. What about you?

3

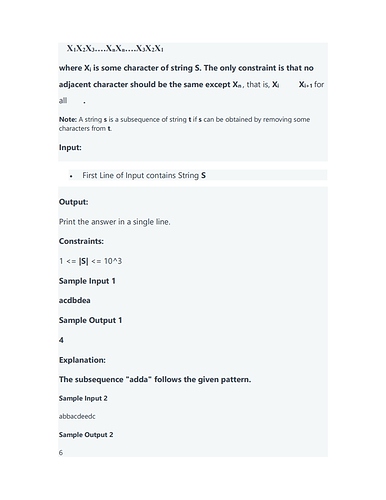
Can you please share your approach for third one?

4

Just LPS… longest palindromic subsequence… used a bottom up approach to fill the dp[][]… The most important thing is you need to know your previous element… store it in a temp variable and do it

2 Likes
5

Anyone knows approach for the second problem?

6

I guess it’s Stirling number and Modulo inverse… recursively we can find modulo inverse … like… 2^-1(mod 10^9+7) ll be like 10^9+7=2(some number)+the remainder you add to get 10^9+7… I m not sure. Maybe.

1 Like
7

I found the answer using contribution technique and it turned out to be summation of (1/i) with i ranging from 1 to N. (Hint : Represent the sequence as a permutation of 1 to N and find contribution of each position as a winning position. )

2 Likes
8

Can anyone please share the approach of fourth problem ?

9

What was the time complexity of your approach for third problem ?

10

N^2 prolly

11

O(26 *N *N)

12

From where did you guys get to know about the contest?
They didn’t update the website, I mean if you go to the hiring events page it still mentions some competition of September’19.

13

I think you must be frequent visitor of hackerrank or should have a friend like that😁

14

Codenation 2020 Questions

page1
page1.jpg816×1056 97.6 KB
page2
page2.jpg816×1056 249 KB
page3
page3.jpg816×1056 123 KB
page4
page4.jpg816×1056 164 KB
page5
page5.jpg816×1056 62 KB

8 Likes
15

Please provide solutions with code.:slightly_smiling_face:

1 Like
16

Isn’t it N²?

17

3rd one :slight_smile:

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define krishwish ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define localin freopen(“in.txt”,“r”,stdin);
#define localout freopen(“out.txt”,“w”,stdout);
const int MAX=2e5+5;
#define ld long double
#define endl “\n”
#define pb push_back
#define ff first
#define ss second
#define vi vector
#define all(v) v.begin(),v.end()
#define rtcheck cout<<“krish\n”;exit(0);
#define vcheck(x) cout<<#x<<" "<<x<<endl;
#define pii pair<int,int>
#define forn for(int i=0;i<n;i++)
const int modu=1e9+7;
const int inf=1e17;
string s;
int dp[1005][1005][27];
int fun(int i,int j,int pre)
{
if(i>j||i==j)
return 0;
if(s[i]==s[j]&&s[i]-‘a’!=pre&&i+1==j)
return 2;
if(dp[i][j][pre]!=-1)
return dp[i][j][pre];
if(s[i]==s[j]&&pre!=s[i]-‘a’)
{
int r= max(fun(i+1,j,pre),fun(i,j-1,pre));
return dp[i][j][pre]=max(2+fun(i+1,j-1,s[i]),r);
}

else
{
    return dp[i][j][pre]=max(fun(i+1,j,pre),fun(i,j-1,pre));
}

}
int32_t main()
{
krishwish;
localin
localout
memset(dp,-1,sizeof(dp));
cin>>s;
int n=s.size();
cout<<fun(0,n-1,26);

}

1 Like
18

I just wrote 26 because it is an appreciable factor, and there could be a huge difference in execution time between a code that does (2-3)NN operations and 26(N*N) operations.

1 Like
19

Can anyone explain the solution to the 4th one?

20

can you explain it better?