PROBLEM LINK:
Contest Division 1
Contest Division 2
Contest Division 3
Practice
Setter: Chaithanya Shyam D
Tester: Manan Grover and Samarth Gupta
Editorialist: Taranpreet Singh
DIFFICULTY
Medium
PREREQUISITES
Convex Hull and geometry, Binary Search.
PROBLEM
Given a set P containing N points in the 2D plane, consider the set S of midpoints of the line joining each pair of distinct points in P. Find the number of points in the convex hull formed by the points in S.
QUICK EXPLANATION
- Build a convex hull of the given set of points. The midpoints of adjacent points in the convex hull shall be part of S.
- Considering the triangle formed by every triplet of points in convex hull when sorted in counter-clockwise order, Only the points in the triangle can appear as part of convex hull of S.
- The total number of times a point is considered is 4 over all triangles.
EXPLANATION
Geometry aspect
Considering convex polygon ABCDEFG, let’s mark the midpoint of each edge of this polygon, and join them. We get polygon HIJKLMN. We can see that points on this polygon would be a part of S. The question remains, which more points?
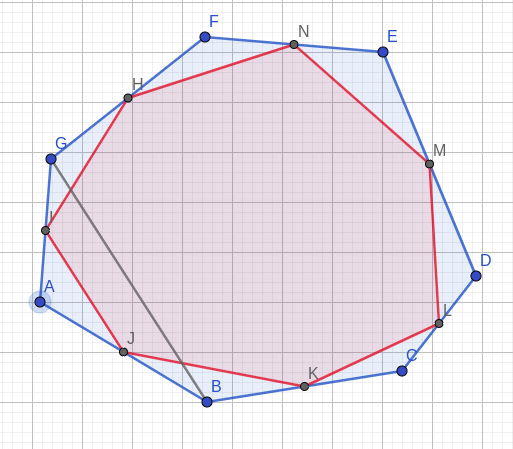
Now we are only interested in pairs of points, which may appear inside triangles AIJ, BJK, and so on. No point inside HIJKLMN matters, and no point can appear outside ABCDEFG.
Let’s consider point A. We want the midpoint to be in region AIJ. Since I is midpoint of AG and J is midpoint of AB, the triangles AIJ and AGB are similar. Also, |AG| = 2*|AI| and |AB| = 2*|AJ|, so we can easily prove that for any point P outside AGB, the midpoint of AP cannot lie inside AIJ.
Programming aspect
We would maintain a set of points S which would contain all possible points which may lie on convex hull. After adding all candidates, we’d run the convex hull algorithm to build hull and print the number of points. So we need to add the candidates to S.
We know that we need to consider each point of convex hull, and the triangle formed by that point, and adjacent points. If we can somehow find the list of points lying inside triangle AGB, then we can iterate on it and compute midpoint of segment formed by each point with A.
But it’s a non-trivial query to find all points lying inside a triangle. But we can relax the condition.
Let’s assume (x_1, y_1), (x_2, y_2) and (x_3, y_3) be the triangle we are considering. All the points lying inside this triangle shall have their x-coordinates in range [min(x_1, x_2, x_3), max(x_1, x_2, x_3)]. Let’s just consider all points having their x-coordinates in this range.
For this, we can first build the convex hull and then keep a list of points sorted by x-coordinate so that all points having x coordinate in some range [L, R] lie in a consecutive segment in list, which we can find by binary search. We consider each pair of points and add their midpoint to S.
What’s the maximum number of pairs we’d consider?
Though it seems quadratic, we can prove that no point inside hull shall be considered more than four times.
With our triangles approach, if we consider the intersection of triangles AGB and triangle BAC, only one triangular region is shared. We can prove that no point appears in more than two triangles. Hence, if we could query the set of points in a triangle easily, then each point would have been considered at most 2 times.
After considering each point with x-coordinate in some range, we are checking some extra points. Let’s separate out upper and lower hull and let’s focus only on ABCD. We can see that x coordinate only increases as we move on the points of this hull. So the ranges of x coordinates covered do not overlap.
For example, for triangle ABC, we’d consider all points with x coordinate in range [A.x, C.x]. Then for triangle BCD, we’d consider all points with x coordinates in range [B.x, D.x]. We can see that strip [B.x, C.x] is covered twice. We can also see that there’s no other triangle in lower hull that can cover any point with x coordinate in range [B.x, C.x].
So, each point is considered at most twice when considering lower hull. Similar explanation follows for upper hull. Hence, each point is considered at most 4 times.
Implementation summary
- Build the convex hull H
- Maintain a list of points P sorted by x coordinates
- Maintain a set of candidates S.
- Consider each point X on H and find the range of points in list P to be considered.
- Add midpoint of segment formed by X with each point in range.
- After processing all points on H, compute the convex hull of S and print the number of vertices in hull.
Implementation tip
Scale all points by a factor of 2 (simply multiplying all coordinates by 2) so that all midpoints have integer coordinates. We can see that it doesn’t affect the relative structure or the number of points at all.
TIME COMPLEXITY
The time complexity is O(N*log(N)) per test case due to sorting and binary search.
SOLUTIONS
Setter's Solution
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#include <bits/stdc++.h>
//#include <ext/pb_ds/assoc_container.hpp> //required
//#include <ext/pb_ds/tree_policy.hpp> //required
//using namespace __gnu_pbds; //required
using namespace std;
//template <typename T> using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
// ordered_set <int> s;
// s.find_by_order(k); returns the (k+1)th smallest element
// s.order_of_key(k); returns the number of elements in s strictly less than k
#define pb(x) push_back(x)
#define mp(x,y) make_pair(x,y)
#define all(x) x.begin(), x.end()
#define print(vec,l,r) for(int i = l; i <= r; i++) cout << vec[i] <<" "; cout << endl;
#define input(vec,N) for(int i = 0; i < (N); i++) cin >> vec[i];
#define debug(x) cerr << #x << " = " << (x) << endl;
#define leftmost_bit(x) (63-__builtin_clzll(x))
#define rightmost_bit(x) __builtin_ctzll(x) // count trailing zeros
#define set_bits(x) __builtin_popcountll(x)
#define pow2(i) (1LL << (i))
#define is_on(x, i) ((x) & pow2(i)) // state of the ith bit in x
#define set_on(x, i) ((x) | pow2(i)) // returns integer x with ith bit on
#define set_off(x, i) ((x) & ~pow2(i)) // returns integer x with ith bit off
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
typedef long long int ll;
typedef long double ld;
const int MOD = 1e9+7; // 998244353;
const int MX = 2e5+5;
const ll INF = 1e18; // not too close to LLONG_MAX
const ld PI = acos((ld)-1);
const int dx[4] = {1,0,-1,0}, dy[4] = {0,1,0,-1}; // for every grid problem!!
// highly risky #defines
#define int ll // disable when you want to make code a bit faster
#define endl '\n' // disable when dealing with interactive problems
typedef pair<int,int> pii;
struct pt {
int x, y;
pt(){}
pt(int xx, int yy){
x = xx;
y = yy;
}
pt(pii p){
x = p.first;
y = p.second;
}
};
bool cmp(pt a, pt b) {
return a.x < b.x || (a.x == b.x && a.y < b.y);
}
bool cw(pt a, pt b, pt c, int f) {
if(f == 1)
return a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y) < 0;
else
return a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y) <= 0;
}
bool ccw(pt a, pt b, pt c, int f) {
if(f == 1)
return a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y) > 0;
else
return a.x*(b.y-c.y)+b.x*(c.y-a.y)+c.x*(a.y-b.y) >= 0;
}
void convex_hull(vector<pt>& a, int f = 1) { // f != 1 means include collinear points
if (a.size() == 1)
return;
sort(a.begin(), a.end(), &cmp);
pt p1 = a[0], p2 = a.back();
vector<pt> up, down;
up.push_back(p1);
down.push_back(p1);
for (int i = 1; i < (int)a.size(); i++) {
if (i == a.size() - 1 || cw(p1, a[i], p2, f)) {
while (up.size() >= 2 && !cw(up[up.size()-2], up[up.size()-1], a[i], f))
up.pop_back();
up.push_back(a[i]);
}
if (i == a.size() - 1 || ccw(p1, a[i], p2, f)) {
while(down.size() >= 2 && !ccw(down[down.size()-2], down[down.size()-1], a[i], f))
down.pop_back();
down.push_back(a[i]);
}
}
a.clear();
for (int i = 0; i < (int)up.size(); i++)
a.push_back(up[i]);
for (int i = down.size() - 2; i > 0; i--)
a.push_back(down[i]);
}
// not strictly
bool inTriangle(pt x, pt A, pt B, pt C){
bool left = false, right = false;
if(cw(x, A, B, 1)) right = true;
else left = true;
if(cw(x, B, C, 1)) right = true;
else left = true;
if(cw(x, C, A, 1)) right = true;
else left = true;
if(right && left) return false;
else return true;
}
int bs(vector<pt> &a, int x){
int N = a.size();
int low = 0, high = N-1;
int ans = N, mid;
while(low <= high){
mid = (low + high)/2;
if(a[mid].x > x){
ans = mid;
high = mid-1;
}
else{
low = mid+1;
}
}
return ans;
}
void solve(){
// Assumptions:
// 1) No duplicate points
// 2) No 3 points such that all 3 are colinear
// 3) Integer coordinates from -1e9 to 1e9
// Here S = a and L = b
int N;
cin >> N;
vector<pt> a(N), b;
// scale the graph by 2
for(int i = 0; i < N; i++){
int x, y;
cin >> x >> y;
a[i].x = 2*x;
a[i].y = 2*y; // scaling so mid point is integer
}
vector<pt> hull = a;
convex_hull(hull, 0);
int M = hull.size();
set<pii> s;
// mid points of consecutive points of the hull
for(int i = 0; i < M; i++){
int mx = (hull[i].x + hull[(i+1)%M].x)/2;
int my = (hull[i].y + hull[(i+1)%M].y)/2;
s.insert({mx, my});
}
sort(all(a), cmp);
for(int i = 0; i < M; i++){
pt A = hull[(i-1+M)%M];
pt B = hull[i];
pt C = hull[(i+1)%M];
int min_x = min({A.x, B.x, C.x});
int max_x = max({A.x, B.x, C.x});
// bs(a, x) finds the smallest i such that a[i].x > x
int left = bs(a, min_x-1), right = bs(a, max_x);
for(int j = left; j < right; j++){
if(inTriangle(a[j], A, B, C)){
int mx = (B.x + a[j].x)/2;
int my = (B.y + a[j].y)/2;
s.insert({mx, my});
}
}
}
for(pii p: s){
// cerr << p.first << " " << p.second << endl;
b.pb(pt(p));
}
convex_hull(b);
cout << b.size() << endl;
}
clock_t startTime;
double getCurrentTime() {
return (double)(clock() - startTime) / CLOCKS_PER_SEC;
}
signed main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
// mt19937_64 rnd(time(NULL));
startTime = clock();
int T = 1;
cin >> T;
while(T--) solve();
cerr << "Time taken = " << getCurrentTime() << endl;
return 0;
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
long long readInt(long long l, long long r, char endd) {
long long x=0;
int cnt=0;
int fi=-1;
bool is_neg=false;
while(true) {
char g=getchar();
if(g=='-') {
assert(fi==-1);
is_neg=true;
continue;
}
if('0'<=g&&g<='9') {
x*=10;
x+=g-'0';
if(cnt==0) {
fi=g-'0';
}
cnt++;
assert(fi!=0 || cnt==1);
assert(fi!=0 || is_neg==false);
assert(!(cnt>19 || ( cnt==19 && fi>1) ));
} else if(g==endd) {
if(is_neg) {
x=-x;
}
assert(l<=x&&x<=r);
return x;
} else {
assert(false);
}
}
}
string readString(int l, int r, char endd) {
string ret="";
int cnt=0;
while(true) {
char g=getchar();
assert(g!=-1);
if(g==endd) {
break;
}
cnt++;
ret+=g;
}
assert(l<=cnt&&cnt<=r);
return ret;
}
long long readIntSp(long long l, long long r) {
return readInt(l,r,' ');
}
long long readIntLn(long long l, long long r) {
return readInt(l,r,'\n');
}
string readStringLn(int l, int r) {
return readString(l,r,'\n');
}
string readStringSp(int l, int r) {
return readString(l,r,' ');
}
void readEOF(){
assert(getchar()==EOF);
}
struct Point {
long long x, y;
bool operator ==(Point a){
return (x == a.x && y == a.y);
}
bool operator <(Point a){
return (x < a.x || (x == a.x && y < a.y));
}
};
//Returns positive value if B lies to the left of OA, negative if B lies to the right of OA, 0 if collinear
int cross(const Point &O, const Point &A, const Point &B)
{
__int128 x = 1, y = 1;
x *= (A.x - O.x);
x *= (B.y - O.y);
y *= (A.y - O.y);
y *= (B.x - O.x);
if(x < y)
return -1;
else if(x > y)
return 1;
return 0;
}
//Returns a list of points on the convex hull
vector<Point> convex_hull(vector<Point> P, int f = 0) // f = 0 means include collinear points
{
int n = P.size(), k = 0;
vector<Point> H(2*n);
sort(P.begin(), P.end());
// Build lower hull
for (int i = 0; i < n; ++i) {
if(f == 1)
while (k >= 2 && cross(H[k-2], H[k-1], P[i]) <= 0) k--;
else
while (k >= 2 && cross(H[k-2], H[k-1], P[i]) < 0) k--;
H[k++] = P[i];
}
// Build upper hull
//i starts from n-2 because n-1 is the point which both hulls will have in common
//t=k+1 so that the upper hull has atleast two points to begin with
for (int i = n-2, t = k+1; i >= 0; i--) {
if(f == 1)
while (k >= t && cross(H[k-2], H[k-1], P[i]) <= 0) k--;
else
while (k >= t && cross(H[k-2], H[k-1], P[i]) < 0) k--;
H[k++] = P[i];
}
//the last point of upper hull is same with the fist point of the lower hull
H.resize(k-1);
return H;
}
int main() {
// your code goes here
int t;
cin >> t;
while(t--){
int n;
cin >> n;
vector<Point> vec;
vector<Point> copy_hull(n);
for(int i = 0; i < n ; i++){
Point p;
cin >> p.x >> p.y;
p.x *= 2, p.y *= 2;
vec.push_back(p);
copy_hull[i] = p;
}
vector<Point> hull = convex_hull(vec);
vector<Point> npts;
int m = hull.size();
sort(copy_hull.begin(), copy_hull.end());
vector<long long> init_x(n);
for(int i = 0; i < n ; i++)
init_x[i] = copy_hull[i].x;
for(int i = 0; i < m ; i++){
// midpoint of i, (i + 1)%m
Point p;
p.x = (hull[i].x + hull[(i+1)%m].x)/2;
p.y = (hull[i].y + hull[(i+1)%m].y)/2;
npts.push_back(p);
long long lo = min({hull[i].x, hull[(i+1)%m].x, hull[(i-1+m)%m].x});
long long hi = max({hull[i].x, hull[(i+1)%m].x, hull[(i-1+m)%m].x});
// consider points in range [lo, hi]
int idx1 = lower_bound(init_x.begin(), init_x.end(), lo) - init_x.begin();
int idx2 = upper_bound(init_x.begin(), init_x.end(), hi) - init_x.begin();
for(int j = idx1 ; j < idx2 ; j++){
if(copy_hull[j] == hull[i])
continue;
p.x = (hull[i].x + copy_hull[j].x)/2;
p.y = (hull[i].y + copy_hull[j].y)/2;
npts.push_back(p);
}
}
sort(npts.begin(), npts.end());
npts.resize(unique(npts.begin(), npts.end()) - npts.begin());
vector<Point> final_hull = convex_hull(npts, 1);
cout << final_hull.size() << '\n';
}
//readEOF();
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
class CONHULK{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int N = ni();
Vector[] P = new Vector[N];
for(int i = 0; i< N; i++)P[i] = new Vector(i, ni()*2, ni()*2);
Vector[] all = new Vector[5*N];
int cnt = 0;
Vector[] outer = convexHull(P);
for(int i = 0; i< outer.length; i++)all[cnt++] = midPoint(outer[i], outer[(i+1)%outer.length]);
Arrays.sort(P, (Vector v1, Vector v2)-> Long.compare(v1.x, v2.x));
for(int i = 0; i< P.length; i++)P[i].ind = i;
int M = outer.length;
for(int i = 0; i< M; i++){
Vector p0 = outer[i], p1 = outer[(i+1)%M], p2 = outer[(i+2)%M];
long minX = Math.min(p0.x, Math.min(p1.x, p2.x)), maxX = Math.max(p0.x, Math.max(p1.x, p2.x));
int left = binarySearch(P, minX-1), right = binarySearch(P, maxX);
for(int j = left; j< right; j++)
if(P[j].ind != p0.ind && P[j].ind != p1.ind && P[j].ind != p2.ind)
all[cnt++] = midPoint(p1, P[j]);
}
Vector[] points = convexHull(Arrays.copyOf(all, cnt));
pn(points.length);
}
void dbg(Object... o){System.err.println(Arrays.deepToString(o));}
//First index i such that P[i].x > x
int binarySearch(Vector[] P, long x){
int lo = 0, hi = P.length;
while(lo < hi){
int mid = lo + (hi-lo)/2;
if(P[mid].x > x)hi = mid;
else lo = mid+1;
}
return hi;
}
Vector midPoint(Vector a, Vector b){
return new Vector((a.x+b.x)/2, (a.y+b.y)/2);
}
Vector[] convexHull(Vector[] p){
Arrays.sort(p, (Vector p1, Vector p2) ->{
if(p1.y!=p2.y)return Long.compare(p1.y, p2.y);
return Long.compare(p1.x, p2.x);
});
Arrays.sort(p, 1, p.length, (Vector p1, Vector p2) -> {
int o = orientation(p[0], p1,p2);
if(o==0)return Long.compare(p[0].dist2(p1), p[0].dist2(p2));
return o;
});
int m = p.length;
Vector[] s = new Vector[m];
int top = 0;
s[top++] = p[0];if(m > 1)s[top++] = p[1];
for(int i = 2; i< m; i++){
while(top>1 && orientation(s[top-2], s[top-1], p[i])!=-1)top--;
s[top++] = p[i];
}
return Arrays.copyOfRange(s, 0,top);
}
// Returns -1 for clockwise, 0 for straight line, 1 for counterclockwise order
int orientation(Vector a, Vector b, Vector c) {
Vector AB = b.add(a.scale(-1));
Vector AC = c.add(a.scale(-1));
long cross = AB.cross(AC);
if(cross < 0)return -1;
if(cross > 0)return 1;
return 0;
}
class Vector {
int ind;
int x, y;
public Vector(int i, int X, int Y){ind = i;x = X;y = Y;}
public Vector(int X, int Y){ind = -1;x = X;y = Y;}
public Vector add(Vector v){return new Vector(x+v.x, y+v.y);}
public Vector scale(int scale){return new Vector(scale*x, scale*y);}
public long cross(Vector v){return x*(long)v.y-y*(long)v.x;}
public long dist2(Vector p){return (x-p.x)*(long)(x-p.x)+(y-p.y)*(long)(y-p.y);}
public String toString(){
return "[ind="+ind+",x="+x+",y="+y+"]";
}
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new CONHULK().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()