PROBLEM LINK:
Author: Arthur Nascimento
Tester: Felipe Mota
Editorialist: Rajarshi Basu
DIFFICULTY:
Medium
PREREQUISITES:
Implementation, Logic, DSU, Small To Large
PROBLEM:
We are given a graph with N \leq 10^5 nodes and M \leq 2*10^5 edges. The graph may have multiple edges between two cities, no self-loops, and might not be connected. We should make a new graph, such that it is connected. Let the degree of each node i before be degPrev_i and the degrees of each node i in the new graph be degNow_i. We have to minimise the value of \sum_{i=1}^{n} |degNow_i - degPrev_i|, which is denoted as the inconvenience.
QUICK EXPLANATION:
How fast can you read this?
- We will have several connected components, some of which are trees, and some which are not trees. First, all the non-tree components can be connected without changing the degree of each node. Just connect one of their non-spanning-tree-edges in cyclic order
- We can use a non-spanning-tree-edge of a non-tree component, and connect a tree component with it without increasing the inconvenience. (Think how)
- We can use a non-spanning-tree-edge of a non-tree component to connect two tree components to it, by adding 2 to the inconvenience.
- If all non-spanning-tree-edges are used up, just add extra edges till everything is connected. Extra edges combine two components at the cost of 2 to the overall inconvenience.
- Maintain the non-spanning-tree-edge information using DSU with Small to Large Merging.
EXPLANATION:
Observation 1
The problem wants us to keep the degrees as similar to the original graph as possible. Thus, it seems that the best thing for us to do is try to keep as many edges of the original graph and make everything connected using as few additional edges/ edge changes possible.
Observation 2
For each of the connected component, it can be of two types. Let us assume that there are C nodes in the component. Then:
- If there are exactly C-1 edges, we call it a tree-component, since it’s in the form of a tree. If we remove any edges, then it no longer remains connected.
- If there are K edges, where K > C-1, then we call it a non-tree component. In particular, there will be K - (C-1) extra edges that, even if removed, will not disconnect the component. We will call all such edge an ExtraEdge.
Observation 3 - Handling Some Simplifications
It’s often a good idea to simplify our problem into smaller and easier parts. For example, here, let’s just assume all our components were either tree components or non-tree components.
- If all were Tree components, and there were x of them, the best-case scenario is adding x-1 new edges to make everything connected, thereby adding a total of 2*(x-1) to the total inconvenience.
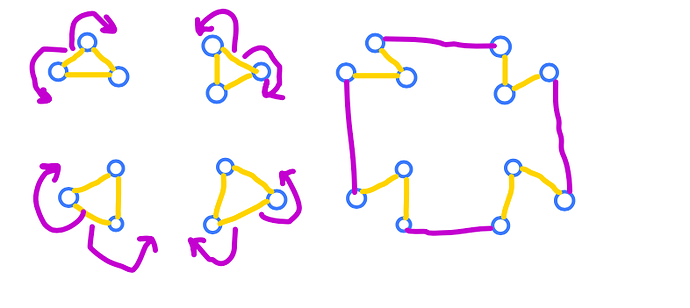
- What if all the component’s are non-Tree components? Well, just take one ExtraEdge from each component, and use them to connect the components in a cycle order.
Confused with connecting the Non-Tree Components?
Here, see this diagram. Hopefully, it will clear things up. The left side has 4 non-tree component, while the right side shows how they can be cyclically connected. (If it reminds you of the Transition State of Wittig Reaction, I am sorry for the PTSD).
Observation 4
Let’s get back to the original problem.
After connecting all the Non-Tree Components into a single (super) Non-Tree component (exercise: figure out why they will still be non-tree, hint: see diagram in Observation 3), we’ll still have some Tree Components left.
Now, we can connect a Tree Component with the (super) Non-Tree Component, by using an ExtraEdge, without adding any inconvenience.
We will call this Operation 1
We love diagrams so here is another
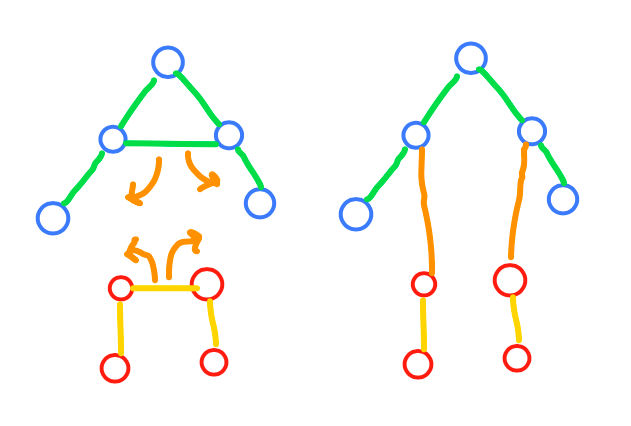
EdgeCase?
To do this operation, we need atleast 2 nodes in the component.
Observation 5
In Operation 1, we connected a single Tree Component to the super NonTree component by using 1 ExtraEdge. However, can we add two Tree components by using 1 ExtraEdge?
We will call this Operation 2
EdgeCase
There aren’t any. Even if there is exactly 1 node in the component, this operation is possible.
Observation 6
What if we exhaust all ExtraEdges? Well, we can just add new edges to connect each Tree Component to the super- NonTree Component. Each of these adds 2 to the total inconvenience.
We will call these Operation 3
Putting Everything together
So here is what we will do:
- First, we form the super-Non-Tree component.
- Next, we do Operation 1 as long as possible. Thus, we either run out of Tree components, in which case we are done, or we run out of ExtraEdges.
- In case we run out of ExtraEdges, keep doing Operation 3 till everything becomes connected.
Wait, we never use Operation 2?
TL;DR: No.
Here's why
Let’s say we have x ExtraEdges and y Tree Components. Now, let us assume y>x since that is the only interesting case. The only difference between Operation 1 and Operation 2 is that, Operation 1 connects 1 Tree component with 0 inconvenience while Operation 2 connects 2 Tree components to the super Non Tree Component with total cost of 2. Each of them use up 1 ExtraEdge. Further, in both cases, we need to use Operation 3 to connect the remaining stuff.
- Now, if we used Operation 1 x times, our total inconvenience = x*0 + (y-x)*2
\implies inconvenience = 2*y - 2*x.- If we used Operation 2 z times, and Operation 1 (x-z) times, then
inconvenience = (x-z)*0 + z*2 + (y - 2*z - (x-z))*2
\implies inconvenience= 2*z + 2*(y-2*z - x + z)
\implies inconvenience= 2*z + 2*(y-z-x)
\implies inconvenience= 2*z + 2*y - 2*z - 2*x
\implies inconvenience= 2*y - 2*x.- Hence we see that we obtain the same inconvenience whether or not we use any Operation 2.
Implementation
First, maintain all the ExtraEdges for the components in the graph using DSU and small-to-large merging inside the DSU (see Editorialist code for details).
Also maintain the adjacency lists of all the nodes as multisets.
Lastly, do all the operations by just iterating over the list of ExtraEdges and Tree components. Again, see Editorialist code for more details.
Time Complexity
Since we are using multiple operations using sets, and small-to-large inside the DSU, our overall complexity is O(nlogn).
QUICK REMINDERS:
There can be multi-edges remember? Don’t forget to use multiset instead of set to represent the adjacency lists.
C++ NOTE: While erasing in a multiset, we have to pass in an iterator to delete one occurrence. If we just pass a value, the multiset erases all the occurrences of the value.
SOLUTIONS:
Setter's Code
#include <bits/stdc++.h>
using namespace std;
int main(){
int t;
cin >> t;
while(t--){
int n, m;
cin >> n >> m;
vector<int> uf(n);
iota(uf.begin(), uf.end(), 0);
vector<vector<pair<int,int>>> indep(n), spanning(n);
function<int(int)> find = [&](int x){
return x == uf[x] ? x : uf[x] = find(uf[x]);
};
auto merge = [&](vector<pair<int,int>> &a, vector<pair<int,int>> &b){
if(a.size() < b.size()){
for(auto & e : a) b.push_back(e);
swap(a, b);
} else {
for(auto & e : b) a.push_back(e);
}
b.clear();
};
auto join = [&](int u, int v){
int fu = find(u);
int fv = find(v);
if(fu == fv){
indep[fu].push_back({u, v});
} else {
spanning[fu].push_back({u, v});
merge(indep[fu], indep[fv]);
merge(spanning[fu], spanning[fv]);
uf[fv] = fu;
}
};
int incovenience = 0;
auto incov_join = [&](int u, int v){
u = find(u);
v = find(v);
if(indep[u].size() < indep[v].size()) swap(u, v);
if(indep[u].size() + indep[v].size() == 0){
incovenience += 2;
spanning[u].push_back({u, v});
merge(spanning[u], spanning[v]);
} else {
auto edge_u = indep[u].back(); indep[u].pop_back();
if (indep[v].empty()) {
auto edge_v = spanning[v].back(); spanning[v].pop_back();
spanning[u].push_back({edge_u.first, edge_v.first});
spanning[u].push_back({edge_u.second, edge_v.second});
} else {
auto edge_v = indep[v].back(); indep[v].pop_back();
spanning[u].push_back({edge_u.first, edge_v.first});
indep[u].push_back({edge_u.second, edge_v.second});
}
merge(spanning[u], spanning[v]);
merge(indep[u], indep[v]);
}
uf[v] = u;
};
vector<int> deg(n);
for(int i = 0; i < m; i++){
int u, v;
cin >> u >> v;
u--; v--;
join(u, v);
deg[u]++;
deg[v]++;
}
vector<pair<int,int>> comp;
vector<int> nodes;
for(int i = 0; i < n; i++) if(i == uf[i] && spanning[i].empty()) {
nodes.push_back(i);
}
for(int i = 0; i < n; i++) if(i == uf[i] && !spanning[i].empty()) {
comp.push_back({indep[i].size(), i});
}
if (comp.empty()) {
cout << (n - 1) * 2 << ' ' << n - 1 << '\n';
for(int i = 1; i < n; i++){
cout << nodes[0] + 1 << ' ' << nodes[i] + 1 << '\n';
}
continue;
}
sort(comp.rbegin(), comp.rend());
for(int i = 1; i < comp.size(); i++){
incov_join(comp[0].second, comp[i].second);
}
int root = find(comp[0].second);
while(indep[root].size() > 0 && nodes.size() >= 2){
auto edge_i = indep[root].back(); indep[root].pop_back();
int u = nodes.back(); nodes.pop_back();
int v = nodes.back(); nodes.pop_back();
spanning[root].push_back({u, edge_i.first});
spanning[root].push_back({v, edge_i.second});
incovenience += 2;
}
if(nodes.size()){
spanning[root].push_back({root, nodes.back()});
incovenience += 2;
}
merge(spanning[root], indep[root]);
cout << incovenience << ' ' << spanning[root].size() << '\n';
for(auto e : spanning[root]){
deg[e.first]--;
deg[e.second]--;
assert(e.first != e.second);
cout << e.first + 1 << ' ' << e.second + 1 << '\n';
}
int res = 0;
for(int i = 0; i < n; i++)
res += abs(deg[i]);
assert(res == incovenience);
}
return 0;
}
Tester's Code
#include <bits/stdc++.h>
using namespace std;
int main(){
int t;
cin >> t;
while(t--){
int n, m;
cin >> n >> m;
vector<int> uf(n);
iota(uf.begin(), uf.end(), 0);
vector<vector<pair<int,int>>> indep(n), spanning(n);
function<int(int)> find = [&](int x){
return x == uf[x] ? x : uf[x] = find(uf[x]);
};
auto merge = [&](vector<pair<int,int>> &a, vector<pair<int,int>> &b){
if(a.size() < b.size()){
for(auto & e : a) b.push_back(e);
swap(a, b);
} else {
for(auto & e : b) a.push_back(e);
}
b.clear();
};
auto join = [&](int u, int v){
int fu = find(u);
int fv = find(v);
if(fu == fv){
indep[fu].push_back({u, v});
} else {
spanning[fu].push_back({u, v});
merge(indep[fu], indep[fv]);
merge(spanning[fu], spanning[fv]);
uf[fv] = fu;
}
};
int incovenience = 0;
auto incov_join = [&](int u, int v){
u = find(u);
v = find(v);
if(indep[u].size() < indep[v].size()) swap(u, v);
if(indep[u].size() + indep[v].size() == 0){
incovenience += 2;
spanning[u].push_back({u, v});
merge(spanning[u], spanning[v]);
} else {
auto edge_u = indep[u].back(); indep[u].pop_back();
if (indep[v].empty()) {
auto edge_v = spanning[v].back(); spanning[v].pop_back();
spanning[u].push_back({edge_u.first, edge_v.first});
spanning[u].push_back({edge_u.second, edge_v.second});
} else {
auto edge_v = indep[v].back(); indep[v].pop_back();
spanning[u].push_back({edge_u.first, edge_v.first});
indep[u].push_back({edge_u.second, edge_v.second});
}
merge(spanning[u], spanning[v]);
merge(indep[u], indep[v]);
}
uf[v] = u;
};
vector<int> deg(n);
for(int i = 0; i < m; i++){
int u, v;
cin >> u >> v;
u--; v--;
join(u, v);
deg[u]++;
deg[v]++;
}
vector<pair<int,int>> comp;
vector<int> nodes;
for(int i = 0; i < n; i++) if(i == uf[i] && spanning[i].empty()) {
nodes.push_back(i);
}
for(int i = 0; i < n; i++) if(i == uf[i] && !spanning[i].empty()) {
comp.push_back({indep[i].size(), i});
}
if (comp.empty()) {
cout << (n - 1) * 2 << ' ' << n - 1 << '\n';
for(int i = 1; i < n; i++){
cout << nodes[0] + 1 << ' ' << nodes[i] + 1 << '\n';
}
continue;
}
sort(comp.rbegin(), comp.rend());
for(int i = 1; i < comp.size(); i++){
incov_join(comp[0].second, comp[i].second);
}
int root = find(comp[0].second);
while(indep[root].size() > 0 && nodes.size() >= 2){
auto edge_i = indep[root].back(); indep[root].pop_back();
int u = nodes.back(); nodes.pop_back();
int v = nodes.back(); nodes.pop_back();
spanning[root].push_back({u, edge_i.first});
spanning[root].push_back({v, edge_i.second});
incovenience += 2;
}
if(nodes.size()){
spanning[root].push_back({root, nodes.back()});
incovenience += 2;
}
merge(spanning[root], indep[root]);
cout << incovenience << ' ' << spanning[root].size() << '\n';
for(auto e : spanning[root]){
deg[e.first]--;
deg[e.second]--;
assert(e.first != e.second);
cout << e.first + 1 << ' ' << e.second + 1 << '\n';
}
int res = 0;
for(int i = 0; i < n; i++)
res += abs(deg[i]);
assert(res == incovenience);
}
return 0;
}
Editorialist's Code
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <vector>
#include <algorithm>
#include <fstream>
#include <queue>
#include <deque>
#include <iomanip>
#include <cmath>
#include <set>
#include <stack>
#include <map>
#include <unordered_map>
#define FOR(i,n) for(int i=0;i<n;i++)
#define FORE(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define ld long double
#define vi vector<int>
#define pb push_back
#define ff first
#define ss second
#define ii pair<int,int>
#define iii pair<int,ii>
#define iiii pair<iii,int>
#define pll pair<ll,ll>
#define plll pair<ll,pll>
#define vv vector
#define endl '\n'
using namespace std;
const int MAXN = 100*1000 + 5;
struct DSU{
int parent[MAXN];
vv<ii> extraEdge[MAXN];
DSU(){
FOR(i,MAXN)parent[i] = i;
}
int find(int a){
if(parent[a] != a)parent[a] = find(parent[a]);
return parent[a];
}
bool isSame(int a,int b){
return find(a) == find(b);
}
void merge(int a,int b){
if(isSame(a,b)){
int pa = find(a);
extraEdge[pa].pb({a,b});
}else{
int pa = find(a);
int pb = find(b);
if(extraEdge[pa].size() > extraEdge[pb].size()){
parent[pb] = pa;
for(auto e: extraEdge[pb])extraEdge[pa].pb(e);
}else{
parent[pa] = pb;
for(auto e: extraEdge[pa])extraEdge[pb].pb(e);
}
}
}
};
multiset<int> g[MAXN];
void solve(){
DSU dsu;
int n,m;
cin >> n >> m;
FOR(i,n)g[i].clear();
FOR(i,m){
int a,b;
cin >> a >> b;
a--;b--;
dsu.merge(a,b);
g[a].insert(b);
g[b].insert(a);
}
vi allRootsNotTree;
vi allRootsTree;
FOR(i,n){
if(dsu.find(i) == i){
if(dsu.extraEdge[i].empty())allRootsTree.pb(i);
else allRootsNotTree.pb(i);
}
}
vv<ii> allExtraEdges;
vv<ii> newEdges;
int s = allRootsNotTree.size();
if(s > 1){
FOR(i,s){
ii ed = dsu.extraEdge[allRootsNotTree[i]].back();
ii edn = dsu.extraEdge[allRootsNotTree[(i+1)%s]].back();
//cout << ed.ff << " " << ed.ss << endl;
//cout << ed.ff << " " << ed.ss << endl;
g[ed.ff].erase(g[ed.ff].find(ed.ss));
g[ed.ss].erase(g[ed.ss].find(ed.ff));
g[ed.ss].insert(edn.ff);
g[edn.ff].insert(ed.ss);
if(i == 0)allExtraEdges.pb({edn.ff,ed.ss});
}
}
if(s > 1){
FOR(i,s)dsu.extraEdge[allRootsNotTree[i]].pop_back(); // since all these were already used.
}
FOR(i,s){
for(auto e : dsu.extraEdge[allRootsNotTree[i]]){
allExtraEdges.pb(e);
}
}
int x = 0;
vi listOf1Nodes;
while(!allExtraEdges.empty()){
auto e = allExtraEdges.back();
if(allRootsTree.empty())break;
int item = allRootsTree.back();allRootsTree.pop_back();
if(g[item].empty())listOf1Nodes.pb(item);
else{
int nitem = *(g[item].begin());
g[item].erase(g[item].find(nitem));
g[e.ff].erase(g[e.ff].find(e.ss));
g[e.ss].erase(g[e.ss].find(e.ff));
g[nitem].erase(g[nitem].find(item));
g[item].insert(e.ff);
g[e.ff].insert(item);
g[nitem].insert(e.ss);
g[e.ss].insert(nitem);
allExtraEdges.pop_back();
}
}
for(auto e : listOf1Nodes)allRootsTree.pb(e);
for(auto e : allExtraEdges){
if(allRootsTree.size() == 0){
break;
}
if(allRootsTree.size() == 1){
g[e.ff].erase(g[e.ff].find(e.ss));
g[e.ss].erase(g[e.ss].find(e.ff));
int root1 = allRootsTree.back();allRootsTree.pop_back();
g[e.ff].insert(root1);
g[e.ss].insert(root1);
g[root1].insert(e.ff);
g[root1].insert(e.ss);
x+=2;
break;
}
g[e.ff].erase(g[e.ff].find(e.ss));
g[e.ss].erase(g[e.ss].find(e.ff));
int root1 = allRootsTree.back();allRootsTree.pop_back();
int root2 = allRootsTree.back();allRootsTree.pop_back();
g[e.ff].insert(root1);
g[e.ss].insert(root2);
g[root1].insert(e.ff);
g[root2].insert(e.ss);
x+=2;
}
//cout << "SSGDFg" << endl;
int root1;
if(allRootsNotTree.empty())root1 = allRootsTree[0];
else root1 = allRootsNotTree[0];
for(auto e : allRootsTree){
if(allRootsNotTree.empty() and e == allRootsTree[0])continue;
x += 2;
g[e].insert(root1);
g[root1].insert(e);
}
vv<ii> allEdges;
FOR(i,n){
for(auto e: g[i]){
if(i < e){
allEdges.pb({i,e});
}
}
}
cout << x << " " << allEdges.size() << endl;
for(auto e: allEdges){
cout << e.ff+1 << " " << e.ss+1 << endl;
}
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)solve();
return 0;
}
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()



 )
)