Problem : link
Solution approach:
sorted wrt cmp and computed final value in that order
bool cmp(const pii a1 , const pii a2)
{
if(a1.second * a2.first + a2.second > a1.first * a2.second+a1.second)
return true;
else
return false;
}
Need help for correctness proof
Thanks in advance
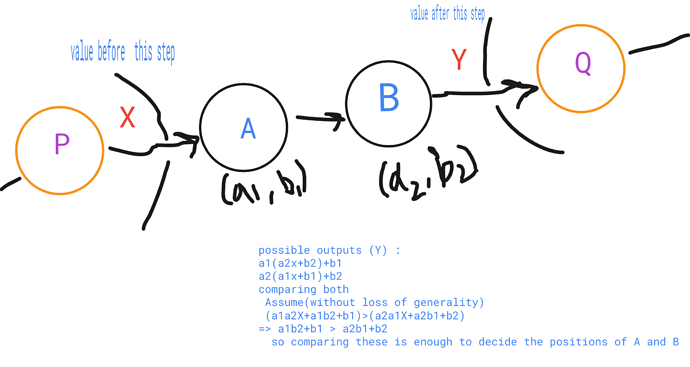
a1(a2x+b2)+b1
a2(a1x+b1)+b2
comparing both
a1a2x+a1b2+b1>a2a1x+a2b1+b2
hence
a1b2+b1>a2b1+b2
Hope you understand
@rishabhag_007 yeah! got that bro, thanks!!
I thought I need some more satisfying proof and posted it here.
Its more like a greedy approach. Select the best amplifier first.
Select the best at beginning or in last???
I think best is selected at last…
Correct me if I’m wrong
@rishabhag_007 How you come up with the first two equations:
a_1 \times (a_2x+b_2) + b_1 \cdots (i)
a_2\times(a_1x+b_1) + b_2 \cdots (ii)
What were your assumptions ?
I got the (ii) equation, output of the second amplifier can be written in that form, but how about (i)?
Thanks
(a1 , b1) (a2 , b2) take this sequence you will get equation (ii) as output
(a2 , b2) (a1 , b1) take this sequence you will get equation (i) as output
as we have to find the max of all possible permutations of amplifiers
O(N!) – naive solution (considering all sequences)
O(N * N) – Greedy approach as described above