CSES Graphs - Mail Delivery : Help Needed!

1

Question
We just have to find a Euler Circuit in Undirected graph, and i am using heirholzer’s Algorithm but getting TLE in last test case.
Submission
TestCase
Please help me figure out the reason for TLE.
Thanks in advance.!
@vijju123 @ssjgz

2

The problem with your approach is that whenever you are visiting a edge u r not erasing it.
In the worst case you will try to visit already visited edge in your adjacency list which will consume a lot of time and will result in TLE as happened in last test case.

3

But i am using visited array on edges, which will make sure that i don’t visit already visited edges.
isn’t that enough?

4

Not at all
suppose you have k edges which are connected through vertex v.
In each whenever you will visit vertex v you will need O(k) time to traverse it.
If you erase already visited edges then you save upto O(k^2) time as
1+2+3+…k each time you will be skipping 1,2,3,…k edges.

5

Check out my DFS

void dfs(int u)
{
	for(idx[u]; idx[u] < g[u].size(); idx[u]++)
	{	
		int v = g[u][idx[u]];
		int x = u;
		int y = v;
		if(x > y)
		{
			swap(x,y);
		}
		if(edge[x].find(y) == edge[x].end()) continue;

		edge[x].erase(y);
		--degree[u];
		--degree[v];
		dfs(v);
	}
	stck.push(u);
}

See what i did there? I created a global vector idx and did the following to track the edge being currently explored.

for(idx[u]; idx[u] < g[u].size(); idx[u]++)

When I come back, I don’t start checking ALL neighbours of vertex ‘u’. I simply continue from where I left. Hope that makes sense?

If we don’t take care of this, we will search ALL edges every time in the following case. I am calling this graph a flower-with-petal graph. Only seven petals in this graph, but imagine what happens if there are 10^5 petals (with O(N^2) complexity)

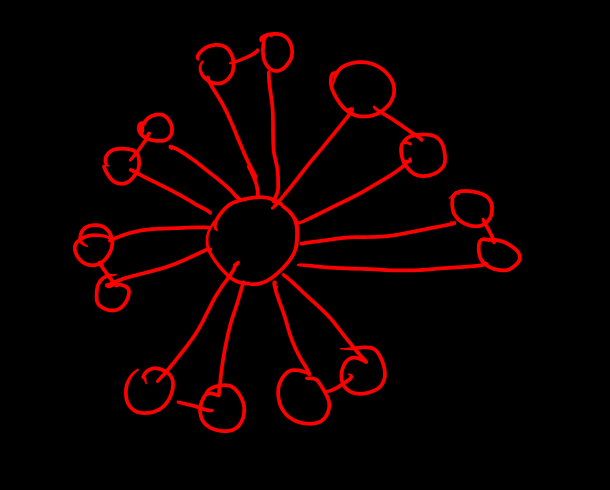
image

If it doesn’t I am not going to type out more here. I try to make a Eulerian Circuit video on priority and explain this aspect clearly.

Watch out for this video series: - YouTube

1 Like
6

Let us say a node a k edges.
Your method takes k^2 time for a node.
Now, if you erase erase a edge every time you visit ,this is what happens u erase a edge as u enter the node and erase another edge as u exit the node , thus saving 3/4 th of the time as time taken would be summation (k-1) + (k-3) +(k-5)…which is nearly 4 times efficient.

1 Like
7

Yes got it…Thanks!

1 Like
8

Thanks for clearing it out…Keep up the good work…!

9

Yes…Thanks

10

I am not able to access the link mentioned. Is it no longer available?