CVCE005 - Editorial

editorial
, ,
1

PROBLEM LINK:

Square Factor Sum - Practice

Author: Muneeb Hussaini
Tester: Srilekhya, Chitturi Sai Suman
Editorialist: Muneeb Hussaini

DIFFICULTY:

Easy

PREREQUISITES:

None

PROBLEM

Given a positive integer n, find the sum of all of its prime factors which are also perfect squares.

QUICK EXPLANATION

This is just an implementation problem. We iterate over i\ \forall\ i \isin[1, \sqrt{N}] and check if i^2 divides N. If i^2 divides N, we add it to our result.

EXPLANATION

The problem can be easily solved by considering that if i^2 is a factor of N, then i is a factor of N as well.
Hence, we need not iterate up to all the factors of N but simply until all factors up to \sqrt{N}.

  • A variable sum is taken to store the sum of the square factors.

  • i is iterated from 1 to \sqrt{N}. If N is divisible by i then i^2 is checked. If i^2 is also a factor of N then sum is incremented by i^2.

ALTERNATIVE EXPLANATION

The given problem can be solved in O(log n) time by using the Smallest Prime Factor concept.
This method removes the need to traverse all i up to \sqrt{N}. The prime factorization of N is obtained using the Smallest Prime Factor concept.

N = 2^a \times 3^b \times 5^\times \dots \times P^p

Using this representation we can find the sum of square factors.
Formula:
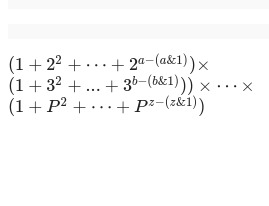
image
Calculating the result becomes easier when we can write each term as a sum of terms in GP.

SOLUTIONS:

Setter's Solution 
import math as m
 
def func():
    n = int(input())
    sqf = []
    for i in range(int(m.sqrt(n)), 1, -1):
        if n%i == 0:
            a = i*i
            if n%a == 0:
                sqf.append(a)
    return sum(sqf) + 1
 
T = int(input())
for i in range(T):
    print(func())

Time Complexity: O(\sqrt{N}) per test case

Tester's Solution, using SPF concept 
from math import sqrt
from collections import defaultdict


def computeSPF():
    # Computes Smallest Prime Factor of all n <= max(N) in (N log N) time
    # Code available in GFG

    size = 10**6 + 2 # Maximum value of N

    # Assume Smallest Prime factor of 'i' is 'i' itself
    spf = [i for i in range(size)]

    # Smallest Prime Factor of any Even Number is 2
    for i in range(2, size, 2):
        spf[i] = 2

    for i in range(3, int(sqrt(size)), 2):
        if spf[i] == i:
            for j in range(i * i, size, i):
                if spf[j] == j:
                    spf[j] = i
                
    return spf


def solve(N, spf):
    # Calculates the Sum of Square Factors of N

    # Stores the powers of prime factors of N
    power = defaultdict(int)

    # Numerator and Denominator for formula
    num = 1
    den = 1

    # Factor N in Logarithmic time
    while N > 1:
        power[spf[N]] += 1
        N //= spf[N]
    
    # Implementation of the formula
    for base in power:
        num *= pow(base ** 2, power[base]//2 + 1) - 1
        den *= base ** 2 - 1

    return num // den



def main():

    spf = computeSPF()

    testcases = int(input())

    for test in range(testcases):
        N = int(input())
        print(solve(N, spf))

Time Complexity: O(\log{N}) per test case

1 Like