PROBLEM LINK:
Author: Tushar Sharma
Tester: Pankaj Sharma
Editorialist: Tushar Sharma
DIFFICULTY:
MEDIUM
PREREQUISITES:
Modular Multiplicative Inverse, Queries of nCr in O(1) time complexity,Fermat’s little theorem
PROBLEM:
Find the number of ways in which in which each team of n and m members could arrange themselves , so that if G and B represents a string , then each prefix of string has more G than B. Then , we need to find the modulo of the “multiplication of both the number of ways” by 10^9+7.
QUICK EXPLANATION:
This problem can be categorized as Dyck language problem. So number of ways for achieving the required condition reduces to 2nCn. So , then we just optimally need to find the multiplication of 2nCn and 2mCn , and its modulo with 10^9+7.
EXPLANATION:
The goal is to find the number of Dyck words with a length of 2n. What is a Dyck word? It’s a string consisting only of n X’s and n Y’s, and matching this criteria: each prefix of this string has more X’s than Y’s. For example, “XXYY” and “XYXY” are Dyck words, but “XYYX” and “YYXX” are not.
(Here X is analogous to Girls and Y to Boys)
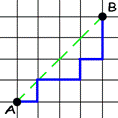
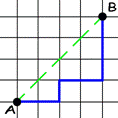
Let’s start the calculation process. We are going to build a geometrical analog of this problem, so let’s consider paths that go from point A(0, 0) to point B(n, n) and do not cross segment AB, but can touch it (see examples for n=4).
We can just build a bijection in such a way: step right – ‘X’, step up – ‘Y’.
Here’s the main idea of the solution: Find the number of paths from A to B that cross segment AB, and call them “incorrect”. If path is “incorrect” it has points on the segment CD, where C = (0, 1), D = (n-1, n). Let E be the point nearest to A that belongs to CD (and to the path). Let’s symmetrize AE, part of our “incorrect” path with respect to the line CD. After this operation we’ll get a path from F = (-1, 1) to B.
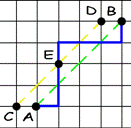
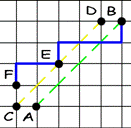
It should be easy to see that, for each path from F to B, we can build only one “incorrect” path from A to B, so we’ve got a bijection. Thus, the number of “incorrect” paths from A to B is 
. Now we can easily get the answer, by subtracting the number of “incorrect” paths from all paths:
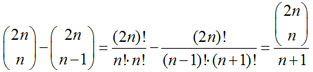
This number is also known as n’s Catalan number.
So, now we know the number of ways for team A and team B are 2nCn and 2mCm respectively.
Now, we need to just multiply both the values of ways and find its modulo 10^9+7.
But as we know , the constraints are too big to follow this Naive approach,
1=T=10^5 & 1=N,M=10^5
So we need an optimized way to calculate nCr % p, and one could notice the constraints, and conclude that an O(1) solution is required to get the solution. One could know the approach to do this by following this link.
The idea behind is nCr can also be written as (n!/(r!*(n-r)!) ) mod p , which is equivalent to (n!*inverse(r!)*inverse((n-r)!) ) mod p . So, precomputing factorial of numbers from 1 to n will allow queries to be answered in O(log n).And, Precompute inverse of factorial in O(n) time and then quereies can be answered in O(1) time. Inverse of 1 to N natural number can be computed in O(n) time using Modular multiplicative inverse.
Using recursive definition of factorial, the following can be written as:
n! = n * (n-1) !
taking inverse on both sides
inverse( n! ) = inverse( n ) * inverse( (n-1)! )
Below is the implemention of the above explanation
SOLUTION:
Editorialist's Solution
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define all(x) (x).begin(), (x).end()
#define trace(...) __f(#__VA_ARGS__, __VA_ARGS__)
template <typename Arg1>
void __f(const char* name, Arg1&& arg1) { cerr << name << " : " << arg1 << '\n'; }
template <typename Arg1, typename... Args>
void __f(const char* names, Arg1&& arg1, Args&&... args) {
const char* comma = strchr(names + 1, ',');
cerr.write(names, comma - names) << " = " << arg1 << " | "; __f(comma + 1, args...);
}
const ll N = 2e5;
const ll MOD = 1e9 + 7;
ll add(ll x, ll y) {ll ans = x + y; return (ans >= MOD ? ans - MOD : ans);}
ll mul(ll x, ll y) {ll ans = x * y; return (ans >= MOD ? ans % MOD : ans);}
ll sub(ll x, ll y) {ll ans = x - y; return (ans < 0 ? ans + MOD : ans);}
vector<ll> fac, fac_inverse, num_inverse;
void preprocess() {
fac = fac_inverse = num_inverse = vector<ll>(N + 1);
num_inverse[0] = num_inverse[1] = 1;
for (ll i = 2; i <= N; i++)
num_inverse[i] = num_inverse[MOD % i] * (MOD - MOD / i) % MOD;
fac_inverse[0] = fac_inverse[1] = 1;
for (ll i = 2; i <= N; i++)
fac_inverse[i] = (num_inverse[i] * fac_inverse[i - 1]) % MOD;
fac[0] = 1;
for (ll i = 1; i <= N ; i++)
fac[i] = (fac[i - 1] * i) % MOD;
}
ll power(ll x, ll y)
{
ll ans = 1;
x = x % MOD;
while (y > 0) {
if (y & 1)
ans = (ans * x) % MOD;
y = y >> 1;
x = (x * x) % MOD;
}
return ans;
}
ll modInverse(ll n)
{
return power(n, MOD - 2);
}
ll nCr( ll n, ll r)
{
if (r == 0)
return 1;
return mul(mul(fac[n], fac_inverse[r]), fac_inverse[n - r]);
}
ll getCatalan(ll n) {
ll ans = mul(nCr(2 * n, n), power(n + 1, MOD - 2));
return ans;
}
void solve() {
ll ans = 0;
ll n, m;
cin >> n >> m;
int max = 1e5;
assert(n >= 1 and n <= max);
assert(m >= 1 and m <= max);
ans = mul(getCatalan(n), getCatalan(m));
cout << ans << "\n";
}
int main()
{
cin.sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
preprocess();
int max = 1e5;
assert(t >= 1 && t <= max);
while (t--)
solve();
return 0;
}
For doubts, please leave them in the comment section, I’ll address them.