DBLDATE - Editorial

editorial
, , , ,
1

PROBLEM LINK:

Practice
Contest

Author: Amit Kumar Ray
Testers: Pankaj Mandrawal
Editorialist: Jatin Khandual

DIFFICULTY:

EASY

PREREQUISITES:

Observations, Basic Math, Ternary Search

PROBLEM:

Given two points P and Q in the coordinate-plane, you need to find a point R on the x-axis that minimizes the overall distance \overline{\rm PR}+\overline{\rm RQ}. Print this optimal distance.

QUICK EXPLANATION:

The point R can be ternary-searched in the interval [0, 1e9]. Alternatively, for two points P(x_1, y_1) and Q(x_2, y_2), the optimal distance is equivalent to \overline{\rm P'Q} where P'(x_1, -y_1) is the reflection of P across the x-axis.

EXPLANATION:

It is not difficult to see that the distances \overline{\rm PR}+\overline{\rm RQ} for all R whose x-coordinate lies in the range [0, 1e9] follows a parabolic curve (i.e. it is unimodal) in that it first decreases to reach a minimum and then increase again. The point where the curve attains its minimum can be found with ternary search under the given time-limit.

Note: It takes about 200-300 iterations (independent of the interval limits) per test case to achieve a precision of about 10^{-6}.

ALTERNATE EXPLANATION:

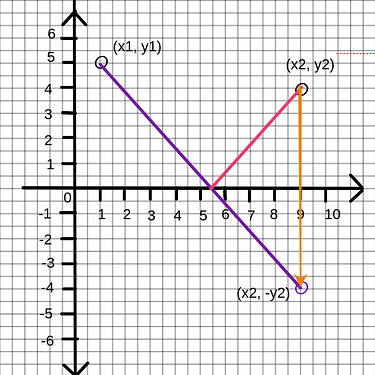
Alternatively, for two points P(x_1, y_1) and Q(x_2, y_2), the optimal distance is equivalent to \overline{\rm P'Q} where P'(x_1, -y_1) is the reflection of P across the x-axis.

Test
Test565×563 50.2 KB

SOLUTIONS:

Setter's Solution 
//“Make it work, make it right, make it fast.” – Kent Beck
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef long double dd;
const int siz = 1e6 + 5;
const int MOD = 1e9 + 7;
#define endl '\n'
#define deb(x) cout << #x << " = " << x << endl;

void solve(){
  long double x, y, X, Y;
  cin >> x >> y >> X >> Y;
  assert(x >= 0 and x <= 1e9);
  assert(y >= 0 and y <= 1e9);
  assert(X >= 0 and X <= 1e9);
  assert(Y >= 0 and Y <= 1e9);
  long double ans = 0;
  Y = -Y;
  ans = sqrtl(((X-x)*(X-x)) + ((Y-y)*(Y-y)));
  cout << fixed << setprecision(7) << ans << endl;
}

int main(){
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  int t = 1;
  cin >> t;
  assert(t >= 1 and t <= 1e5);
  while(t--){
    //tt++;
    //cout << "Case #" << tt << ": ";
    solve();
  }
  return 0;
}
Editorialist's Solution 
//author: hitch_hiker42;
#include<bits/stdc++.h>
using namespace std;

//solution:
void hike() {
    int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
    double lo = 0, hi = 1e9;
    auto f = [&](double m) {
        return hypot(x1 - m, y1) + hypot(x2 - m, y2);
    };
    while(hi - lo > 1e-6) {
        double mid1 = lo + (hi - lo) / 3;
        double mid2 = hi - (hi - lo) / 3;
        double f1 = f(mid1), f2 = f(mid2);
        if(f1 < f2) hi = mid2;
        else lo = mid1;
    }
    cout << fixed << setprecision(7) << f(lo) << "\n";
}

signed main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr); cout.tie(nullptr);
    int t; cin >> t;
    while(t--) hike();
    return 0;
} //farewell, until we meet again..
3 Likes