Here are solutions to the recent December Lunch Time Div 2 Complete. I didn’t understand STICK2, TREEQ1 so If anyone would like to add those two into it, I’d really appreciate that.
PROBLEM 1: CHEALG
Do as the question says, create such string check if it’s size is less then original string, if yes print “YES” otherwise “NO”. I used a string stream because it writes into a stringbuffer, which usually means a linked list of buffers. Memory is not continuous, and it requires no reallocation as the buffer grows.
solution: CodeChef: Practical coding for everyone
PROBLEM 2: STUPMACH
For a range 0…R we cannot have more than min(0…R) in all the boxes collectively. If we keep calculating minimum for every next range and update for each ith box the best we can do to be min(0…i) and finally we just need to add the best we can get for our answer.
solution: CodeChef: Practical coding for everyone
PROBLEM 3: GUESSNUM
The problem wants us to find N, here d is a divisor of N so we can write N as k.d where k is any ineger since d divides N.
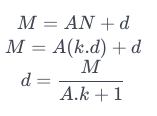
Now if we find out all the divisors of M, which we can find since M is know and then if we equate it to our denominator x = A.k + 1. Where A is known then we will get our value of k. N = k.d so we still need to find d which is M/x where x the divisor of M which we found earlier. Also there could be multiple divisors of M so hence we need to apply our formula for multiple x, hence getting multiple k & d
solution: CodeChef: Practical coding for everyone
PROBLEM 4: EVIPRO
It’s super easy to take 50 points out of this question, a naive N^3 brute force will even pass the solution. For 100 points we need to look for a relation.
The question is asking to find consecutive in the final string u for each L…R and need linear solution. So we get an intuition from here that we want a relation of between regular string and how duplicates in it matches with our final result
case 1: 0010
Here are all possible u we can have for all [L,R]
1010 - 0 A
1110 - 2 B
1100 - 2 C
1101 - 1 D
0110 - 1 E
0100 - 1 F
0101 - 0 G
0000 - 3 H
0001 - 2 I
0011 - 2 J
= 14
‘00’ this duplicate pair will remain duplicate if this range entirely gets flipped to ‘11’ or didn’t get flipped at all and remain ‘00’ which is happening B, C, D, H, I, J. i.e. 6 times so in final ans it will correspond to += 6.
Lets generalise this number 6. Total number of ranges we have is (n*(n+1))/2 since ranges of size n is 1, n-1 is 2, n-2 is 3 and so on till n so summing them up we get it. Now from all range we want to subtract the ones which are partially flipping our ‘00’ duplicate pair. Visualising it is easier that there will be n such pairs one from. So making it overall ans += (n*(n+1))/2 - n
In case the values are not same so ‘01’ then if there’s a partial flip then it can change our value to duplicates ‘00’ ‘11’ and we already calculated how many partial overlaps can be there it is n. So in this case ans += n. In this example B, E, H, I corresponds to it.
solution: CodeChef: Practical coding for everyone
PROBLEM 5: FREQFUN
In this problem there’s originally an array S lets say [0 0 1 2 2 5] and the chef forgets some of its element denoted by -1 giving A [0 0 -1 2 2 5] He made a copy of count for the original array S in B [2 1 2 0 0 1] and based on B he again make a count array from B i.e G [ 2 2 2 0 0 0 0] here G[i] is count of i in array B that’s why it’s length is N+1 because in B it can happen that all elements are same.
Now we are given G and A and we need to find lexiographically smallest S possible in case it’s impossible we just need to print “impossible”
First thing which is pretty obvious that if we sum up all elements of G we should always get n if not then the ans is “impossible”. First thing we can do is we can find an scrambled version of B which is sorted (storing it in multiset) so for the above example it’s 001122. We can also create B based on A (excluding -1s) so for above example we get 2 0 2 0 0 1. Now what we can do is we traverse from end to start in our B array which we created from given A and for every element we try to find it in our scrambled B which we created from G. If we take lower bound and the value matched is lesser means that element isn’t right so we push back that index to our answer.
Finally we traverse our ans list in reverse in order to get the lexiographic smallest answer and we get our answer. Other impossible scenerios can be if the elements in Gs becomes empty then to avoid runtime error print “impossible” and also if we didn’t find answers corresponding to every -1s present that means our G array is contradictory with our A array.
This problem isn’t difficult I found it’s implementation a little difficult. Here’s my solution: CodeChef: Practical coding for everyone