PROBLEM LINK:
Practice
Division 1
Division 2
Author: Sachin Yadav
Tester: Taranpreet Singh
Editorialist: Sachin Yadav
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Graphs, BFS
PROBLEM:
There is a 2d grid with N rows and M columns. Each cell on the grid has some binary-integer either 0 or 1.
For making all cells in the grid same, initially we choose a cell. Now, we repeatedly apply the move on this cell, until the whole grid is filled with same binary number.
In a single move, the binary numbers in all the cells reachable from the given cell are inverted. A cell is called reachable from another cell, if both cells have the same number, and it is possible to move from one cell to the other through cells of that number only, moving vertically and horizontally. If earlier the number was 1, it turns into 0 and vice versa.
Choosing the start cell optimally, can you find the minimum number of moves to make all the cells have same number?
QUICK EXPLANATION:
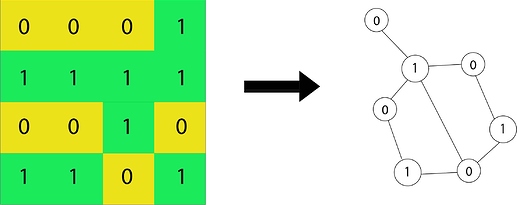
We first create a condensed graph by considering cells of same number which are reachable (refer to problem statement for criteria of reachability) to one another as a single node. We number the nodes on the grid accordingly and consider the edges in the grid between different nodes to form the edges for our new graph. The answer to the problem, is the radius of this new graph formed.
EXPLANATION:
As mentioned above, we would be first converting the grid into a graph, where the cells with same number which are reachable to one another are clubbed together to form nodes for the new graph. For this we do numbering of these clusters and consider the edges between two cells with different numbering as an edge between the two respective nodes in the new graph.
Why we have converted it to a graph here? Because performing the move on any cell in the grid is equivalent to changing the colour of the node it belongs to in the new graph and merging all its immediate neighbouring nodes into it. We will be referring to this move as contracting the graph at that node to which the chosen cell corresponds.
So if we contract the graph again and again at the same node, we notice that the distance of the farthest node from the node in consideration keeps on decreasing by 1 in a single move. The corresponding grid becomes filled with same number when after contracting the graph repetitively at the same node, only a single node remains in the graph i.e. the distance of the farthest node from the chosen node in the graph becomes zero.
Hence, if we choose any node in the graph, the number of moves (contractions) it takes is equal to the distance of fartest node from the chosen node. So optimal solution comes when we choose that node whose distance to its fartest node is the least and the number of moves it takes is equal to that least distance.
So again, the solution corresponding to selecting a node is the distance of the farthest node from it. Hence the answer is the minimum among the maximum distances between the chosen node and all other nodes in the graph. This is the defintion of the radius of graph as well, so the radius of the generated graph gives solution to the problem.
Implementation
For constructing the graph from the grid there can be many approaches. What I have used is travesing over the 2d grid , flood filling the cells ,assigning them different numbers and marking them visited. For creating the adjacency list, we traverse over all the edges in the grid and add the edges to the adjacency list which are between cells of different nuberings here.
As we may be double counting the edges between two nodes several times, we can keep track by using an unordered_sets as an adjacency list. This would complete the graph formation.
We do BFS on every node to find the distance of farthest node from it.The minimum of all gives the radius of the graph.
Time Complexity: O((M\times N)^{2})
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
unordered_map<int, unordered_set<int>> adj_list;
bool is_visited[2501];
int last_vertex, N, M;
pair<bool,int> board[101][101];
int dir[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
void bfs(int i, int j, int clr)
{
queue<pair<int,int>> que;
que.push({i,j});
board[i][j].second=clr;
while(!que.empty())
{
auto p=que.front();
que.pop();
for(int d=0; d<4; d++)
{
int x=p.first+dir[d][0], y=p.second+dir[d][1];
if(x<0 || x==N || y<0 || y==M || board[x][y].second || (board[x][y].first != board[p.first][p.second].first)) continue;
board[x][y].second=clr;
que.push({x,y});
}
}
}
void get_adjlist()
{
last_vertex=0;
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
{
if(board[i][j].second==0)
bfs(i,j,++last_vertex);
}
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
{
if(i && board[i][j].second!=board[i-1][j].second)
{
adj_list[board[i][j].second].insert(board[i-1][j].second);
adj_list[board[i-1][j].second].insert(board[i][j].second);
}
if(j && board[i][j].second!=board[i][j-1].second)
{
adj_list[board[i][j].second].insert(board[i][j-1].second);
adj_list[board[i][j-1].second].insert(board[i][j].second);
}
}
}
int radius_graph()
{
int radius=2*N*M;
for(int vtx=1; vtx<=last_vertex; vtx++)
{
memset(is_visited,0,sizeof(is_visited));
queue<int> que;
int dist=0;
que.push(vtx);
is_visited[vtx]=true;
que.push(-1);
while(!que.empty())
{
int curr_vtx=que.front();
que.pop();
if(curr_vtx==-1)
{
if(!que.empty()){ que.push(-1); dist++; }
else break;
}
for(auto v: adj_list[curr_vtx])
{
if(is_visited[v]==false)
{
que.push(v);
is_visited[v]=true;
}
}
}
radius=min(dist,radius);
}
return radius;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int T; cin>>T;
while(T--)
{
memset(board, 0, sizeof(board));
cin>>N>>M;
for(int i=0; i<N; i++)
for(int j=0; j<M; j++)
cin>>board[i][j].first;
get_adjlist();
cout<<radius_graph()<<"\n";
adj_list.clear();
}
return 0;
}
Tester's Solution
import java.util.*;
import java.io.*;
import java.text.*;
public class Main{
//SOLUTION BEGIN
//Into the Hardware Mode
void pre() throws Exception{}
void solve(int TC)throws Exception{
int n = ni(), m = ni();
hold(1 <= Math.min(n, m) && Math.max(n, m) <= 50);
boolean[][] grid = new boolean[n][m];
int[] set = new int[n*m];
for(int i = 0; i< n; i++){
for(int j = 0; j< m; j++){
grid[i][j] = ni() == 1;
set[i*m+j] = i*m+j;
}
}
for(int i = 0; i< n; i++){
for(int j = 0; j< m; j++){
if(i < n-1 && grid[i][j] == grid[i+1][j])union(set, i*m+j, (i+1)*m+j);
if(j < m-1 && grid[i][j] == grid[i][j+1])union(set, i*m+j, i*m+j+1);
}
}
int[] mp = new int[n*m];
Arrays.fill(mp, -1);
int c = 0;
for(int i = 0; i< n; i++){
for(int j = 0; j< m; j++){
int root = find(set, i*m+j);
if(mp[root] == -1)mp[root] = c++;
mp[i*m+j] = mp[root];
}
}
int[] from = new int[c*c], to = new int[c*c];
int cnt = 0;
boolean[][] connect = new boolean[c][c];
for(int i = 0; i< n; i++){
for(int j = 0; j< m; j++){
if(i < n-1 && grid[i][j] != grid[i+1][j]){
int x = mp[i*m+j], y = mp[(i+1)*m+j];
connect[x][y] = connect[y][x] = true;
}
if(j < m-1 && grid[i][j] != grid[i][j+1]){
int x = mp[i*m+j], y = mp[i*m+j+1];
connect[x][y] = connect[y][x] = true;
}
}
}
for(int i = 0; i< c; i++)
for(int j = i+1; j< c; j++)
if(connect[i][j]){
from[cnt] = i;to[cnt++] = j;
}
int[][] g = makeU(c, from, to, cnt);
int ans = n*m;
Queue<Integer> q = new ArrayDeque<>();
for(int i = 0; i< c; i++){
int[] di = new int[c];
Arrays.fill(di, n*m+1);
di[i] = 0;
q.add(i);
int mx = 0;
while(!q.isEmpty()){
int u = q.poll();
mx = Math.max(mx, di[u]);
for(int v:g[u]){
if(di[v] > di[u]+1){
di[v] = di[u]+1;
q.add(v);
}
}
}
ans = Math.min(ans, mx);
}
pn(ans);
}
int[][] makeU(int n, int[] from, int[] to, int e){
int[][] g = new int[n][];
int[] cnt = new int[n];
for(int i = 0; i< e; i++){
cnt[from[i]]++;
cnt[to[i]]++;
}
for(int i = 0; i< n; i++)g[i] = new int[cnt[i]];
for(int i = 0; i< e; i++){
g[from[i]][--cnt[from[i]]] = to[i];
g[to[i]][--cnt[to[i]]] = from[i];
}
return g;
}
void union(int[] set, int u, int v){
u = find(set, u);v = find(set, v);
set[v] = u;
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
void exit(boolean b){if(!b)System.exit(0);}
long IINF = (long)1e18, mod = (long)1e9+7;
final int INF = (int)1e9, MX = (int)2e6+5;
DecimalFormat df = new DecimalFormat("0.0000000");
double PI = 3.141592653589793238462643383279502884197169399, eps = 1e-7;
static boolean multipleTC = true, memory = false, fileIO = false;
FastReader in;PrintWriter out;
void run() throws Exception{
if(fileIO){
in = new FastReader("C:/users/user/desktop/inp.in");
out = new PrintWriter("C:/users/user/desktop/out.out");
}else {
in = new FastReader();
out = new PrintWriter(System.out);
}
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
hold(1 <= T && T <= 10);
pre();
for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
if(memory)new Thread(null, new Runnable() {public void run(){try{new Main().run();}catch(Exception e){e.printStackTrace();}}}, "1", 1 << 28).start();
else new Main().run();
}
int find(int[] set, int u){return set[u] = (set[u] == u?u:find(set, set[u]));}
int digit(long s){int ans = 0;while(s>0){s/=10;ans++;}return ans;}
long gcd(long a, long b){return (b==0)?a:gcd(b,a%b);}
int gcd(int a, int b){return (b==0)?a:gcd(b,a%b);}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}