DEQUEUE - EDITORIAL

costheta_z · May 28, 2021, 11:52pm

PROBLEM LINK:

Practice
Contest: Division 1
Contest: Division 2
Contest: Division 3

Author: Daanish Mahajan
Tester: Manan Grover
Editorialist: Nandini Kapoor

DIFFICULTY:

Easy

PREREQUISITES:

Arrays, Optimization

PROBLEM:

You are given a doubly ended queue Q of size M containing elements in the range [1,N] atleast once. Find the minimum total number of elements to pop (given we can pop from either side) to get all the N distinct elements in the values we have popped.

QUICK EXPLANATION:

Visualizing the given dequeue as a circular array starting at index 0 and ending at M-1 with 0 and M-1 being next to each other, we will find the smallest sub-array (that must include at least one of the two extreme indices of the array) consisting of all N numbers.

EXPLANATION:

Note: The popping of some elements from the beginning and some from the end in a doubly ended queue can be visualized as the removal of a sub array consisting of one or both of the extreme indices of the array from a circular array. This would help in understanding the aforementioned approach. Thus we will be depicting the given array as circular array for ease in understanding.

We first find the smallest sub array starting at index 0, that contains all numbers from 1 to N and record its size as the answer.

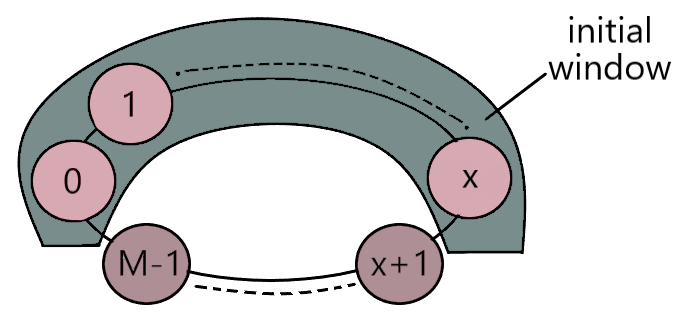depiction Considering 1 to N all numbers are present from indices 0 to X at least once, the initially chosen window would look as above.

We would then remove an element from the rear end of the window, effectively reducing its size by 1 in doing so.

If this removal causes a deficiency of any number from 1 to N (say x) in this new window:
We fulfill this deficit by stretching the window from it’s front end (which expands backwards i.e. initially starting from index 0, we stretch it towards M-1, M-2 and so on - similar to expanding a window in a circular array) to find and accommodate x, thus changing the beginning of the window to index M-i (i being the index at which we found x for the first time while moving in the direction of the expansion of the window), and increasing its size. We then record the answer as the minimum of previous answer obtained and the current window size (window being of the form […, M-2, M-1, 0, 1, …] ).
If the removal of last element from the window has not compromised the appearance of any number from 1 to N:
We record the answer as the size of this new window (as it is guaranteed to be one element smaller than the previous window).

We continue this process of removal and extending window till the index M-1 becomes the rear end of the window (window with rear end M-1 is the last window for which we perform the iteration).

Why stop at this point?

This is because after this point, removing the last element of the window will result in the following 3 possibilities:

Exclusion of both indices 0 and M-1, which was a necessary condition for the sub-arrays we were interested in.

For example in case of Q=[1, 1, 2, 3, 1], N=3, M=5. Initial window being [1, 1, 2, 3, 1] and final one being [1, 1, 2, 3, 1].

Returning to the initial window.

For example in case of Q=[1, 2, 3, 1], N=3, M=4. Initial window being [1, 2, 3, 1] and final one being [1, 2, 3, 1].

Returning to a window including same indices as that of the initial window in a different order.

For example in case of Q=[1, 2, 3, 4], N=4, M=4. Initial window being [1, 2, 3, 4] and final one being [4, 1, 2, 3].

Algorithm for mentioned approach

for i=0 to M:
- if 1 to N all appeared once in Q:
  - window W_1=Q[0], Q[1], ..., Q[i] found

answer= length(window)
ind= index of array at which window ends
end=M-1
x= number of windows found so far

while(ind--):
- if at ind was the only appearance of number Q[ind] in x_th window:
  - while(Q[end]!=Q[ind]):
    - end--
- x++
- window W_x=Q[end], Q[end+1], ..., Q[M-1], Q[0], ..., Q[ind-1], Q[ind] found
- answer=\min (answer, length(W))

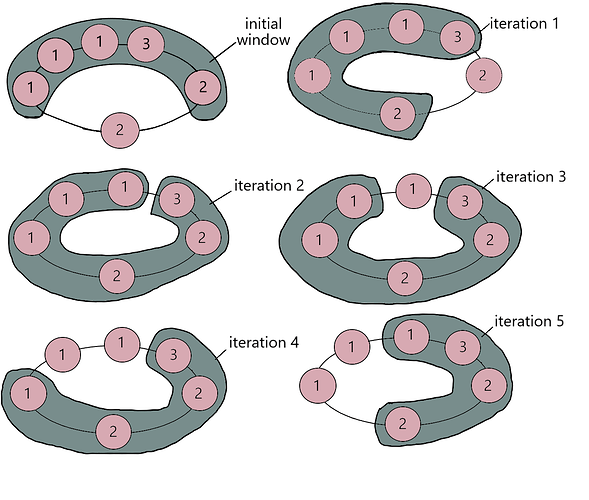
Let us visualize the algorithm with the help of one of the test cases given in the question:

N = 3, M = 6
Q = {1, 1, 1, 3, 2, 2}

The windows found in each of the iterations of the while loop in the algorithm would be as shown in the figure below:

The minimum of all window lengths containing 1 to N numbers at least once is evidently 4, thus the answer is 4.

TIME COMPLEXITY:

O(M) per test case.

SOLUTIONS:

Setter

Tester

    #include <bits/stdc++.h>
    using namespace std;
    int main(){
      ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
      int t;
      cin>>t;
      while(t--){
        int n,m;
        cin>>n>>m;
        int a[m];
        for(int i = 0; i < m; i++){
          cin>>a[i];
        }
        int x = -1;
        map<int, int> mpp;
        for(int i = 0; i < m; i++){
          x++;
          mpp[a[i]]++;
          if(mpp.size() == n){
            break;
          }
        }
        int y = m;
        int ans = x + 1;
        while(x>=0){
          mpp[a[x]]--;
          if(mpp[a[x]] == 0){
            mpp.erase(a[x]);
          }
          x--;
          while(mpp.size() < n){
            y--;
            mpp[a[y]]++;
          }
          ans = min(ans, x + 1 + m - y);
        }
        cout<<ans<<"\n";
      }
      return 0;
    }

Editorialist

    #include<bits/stdc++.h>
    using namespace std;
     
    #define _z ios_base::sync_with_stdio(false); cin.tie(NULL);
    #define int long long int
    #define endl "\n"
    #define mod 1000000007
    #define pb_ push_back
    #define mp_ make_pair
    //______________________________z_____________________________
     
    void solve()
    {
        int n, m;
        cin>>n>>m;
        int a[m], occur[n]={0}, ind=0, ans=m;
        for(int i=0; i<m; i++) {
            cin>>a[i];
            if(!occur[a[i]-1]) ind=i;
            occur[a[i]-1]++;
        }
        ans=ind+1;
        for(int i=ind+1; i<m; i++) {
            occur[a[i]-1]--;
        }
        for(int i=ind, j=m-1; i>=0; i--) {
            occur[a[i]-1]--;
            if(!occur[a[i]-1]) {
                while(a[j]!=a[i]) {
                    occur[a[j]-1]++;
                    j--;
                }
                occur[a[i]-1]++;
                //cout<<i<<" "<<ans<<" "<<m-j+i<<endl;
            }
            ans=min(ans, m-j+i);
        }
        cout<<ans<<endl;
    }
     
    int32_t main()
    {
        _z;
        int t=1;
        cin>>t;
        while(t--)
        {
            solve();
        }
    }

pasricha_dhruv · May 30, 2021, 1:58pm

Great Editorial !
I solved it using binary search on answer and sliding window in O(M*log(M))
Solution: 47074660 | CodeChef

cubefreak777 · May 30, 2021, 2:12pm

It can easily be solved just by using c++ sets in \mathcal{O}(M \log N) code

ashu414 · May 30, 2021, 2:12pm

I was also using binary search but getting wrong answer can you please tell how your isGood function is working

saurabhshadow · May 30, 2021, 2:20pm

Great image explanation!

cfacto · May 30, 2021, 2:20pm

can you pls explain your idea

mainahibtaunga · May 30, 2021, 2:23pm

O(M) solution using 2 pointer technique.

The idea is, there is contiguous block which is never popped. Find the biggest such block!

abhinav520 · May 30, 2021, 3:04pm

I have done using deque and map but it is giving WA, but it is passing most of my trial test cases, please somebody give me some extra testcases where my code fails or tell me what is wrong in this logic
https://www.codechef.com/viewsolution/47095605

thank you

chandan_125 · May 30, 2021, 3:25pm

i am doing this using binary search time complexity will be M logM but it giving TLE can anybody help please , my approach is correct i think there is some mistake in implementation
approach : let say ans is x , then check ans is possible or not if possible the search for below
otherwise for above ans , please help @cubefreak777

code

#include<bits/stdc++.h> 
#define int long long
#define vi vector<int>
#define vii vector<vi>
#define pii pair<int,int>
#define rep(i,a,b) for(int i=a; i<b; i++)
#define rrep(i,a,b) for(int i=a; i>=b; i--)
#define pb(i) push_back(i)
#define all(b) b.begin(),b.end()

// #include <ext/pb_ds/assoc_container.hpp>
// #include <ext/pb_ds/tree_policy.hpp>
// using namespace __gnu_pbds;
using namespace std;
// template<class T> using oset =tree<T, null_type, less_equal<T>, rb_tree_tag,tree_order_statistics_node_update> ;
// st.find_by_order(k); // returns element at position k(0 based indexing)
// st.find_of_key(k); // number of element <k
// st.order_of_key(k); // return order of k 
// less_equal<T> : as multiset
// less<T>      :  only set

const int mod = 1e9 + 7;
const int inf = 1e10 + 20;
const int mxn = 1e5 + 1;
bool check(vector<int>&v,int k,int n){
    int len = v.size();
    int l = 0, r = len - k;
    map<int,int> m;
    for(int i=r; i<len; i++){
        m[v[i]]++;
    }
    if(m.size()==n) return true;
    for(int i=0; i<k; i++){
        int r = len - (k - i);
        m[v[r]]--;
        if(m[v[r]]==0){
            m.erase(v[r]);
        }
        m[v[i]]++;
        if(m.size()==n) return true;
    }

    return m.size()==n;
}
void test_case(){
    int n,m; cin>>n>>m;
    vector<int> v(m,0);
    for(int i=0; i<m; i++){
        cin>>v[i];
    }
    int l = 1, r = m;
    int ans = 0;
    while(l<=r){
        int mid = (l + r)/2;
        if(check(v,mid,n)){
            ans = mid;
            r = mid - 1;
        }
        else{
            l =mid + 1;
        }
    }
    cout<<ans;
}
signed main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int t = 1;  cin>>t;
    while(t--){
        test_case();
        cout<<'\n';
    }
    return 0;
}

jaindiji21 · May 30, 2021, 5:43pm

hey i was also trying to solve the question using the similar greedy approach as you! I took me some time but i found test cases that this method won’t solve.
Try this array and you’ll understand: 1 1 3 1 1 1 2 2

naveen219 · May 30, 2021, 6:11pm

Bro, Can you explain your code?. Your code looks much simpler to me

mihir123568 · May 30, 2021, 6:20pm

I have written the following code with the same kind of approach.
But it gives me WA on the 4th Test case.
can anyone guide me on what may be potentially missing or wrong?
Am I missing a test case or something like that?

CODE:

#include <bits/stdc++.h>
using namespace std;
#define ll              long long int 
#define ld              long double
#define mod             1000000007
#define infinity        1e18
#define endl            "\n"
#define maxValue(var)   numeric_limits<var>::max()
#define minValue(var)   numeric_limits<var>::min()
#define pll             pair<ll, ll>
#define mp              make_pair
#define ff              first
#define ss              second
#define vll             vector<ll>
#define pb              push_back
#define vs              vector<string>
#define ump             unordered_map
#define pq_max(var)     priority_queue <var>
#define pq_min(var)     priority_queue <var, vector<var>, greater<var> >
#define all(v)         v.begin(), v.end()
#define mid(l, r)       (l + (r-l)/2)
#define bitc(x)         __builtin_popcountll(x)
#define fori(i,a,b)     for(int i = (a) ; i < (b) ; i++)
#define foriRev(i,a,b)  for(int i = (a) ; i >= (b) ; i--)
#define iterate(c, it)  for(__typeof(c.begin()) it = c.begin() ; it!= c.end() ; it++)
#define display(args...) { string _s = #args; replace(_s.begin(), _s.end(), ',', ' '); stringstream _ss(_s); istream_iterator<string> _it(_ss); err(_it, args);}
#define displayArr(arr, a, b)   for(int z=(a) ; z<=(b) ; z++) cout << arr[z] << " "; cout << endl;
#define scanVec(vec)         for(int z=(0) ; z<(vec.size()) ; z++) cin >> vec[z];
#define printVec(vec)         for(int z=(0) ; z<(vec.size()) ; z++) cout << vec[z] << " "; cout << endl;

void err(istream_iterator<string> it) {}
template <typename T, typename... Args>
void err(istream_iterator<string> it, T a, Args... args){

    cout << *it << " = " << a << endl;

    err(++it, args...);

}

void fastInOut(){
    // fast input/output
    ios_base::sync_with_stdio(false);
    // NULL <---> 0
    cin.tie(NULL);
    cout.tie(NULL);
}

void myCode(){

    ll tc;   cin >> tc;
    fori(t, 0, tc){
        ll res, n, m; cin >> n >> m;
        res = m;

        vll arr(m); scanVec(arr);
        if(n == m){
            cout << res << endl;
            continue;
        }

        if(n == 1){
            cout << 1 << endl;
            continue;
        }

        ll l = 0;
        ll r = 0;
        unordered_map<int, int> f;
        f[arr[0]]++;

        while (l < m+1){

            while(f.size() != n){
                r++;
                f[arr[(r)%m]]++;
            }

            while(f.size() == n){

                // condition for proper subarray
                if(l%m == 0 or r%m == m-1 or l%m > r%m)
                    res = min(r-l+1, res);
                f[arr[l%m]]--;

                if(f[arr[l%m]] == 0)  f.erase(arr[l%m]);
                l++;
            }
        }
        cout << res << endl;
    }
}

int main(int argc, char const *argv[]){
    fastInOut();
    myCode();
    return 0;
}

cubefreak777 · May 30, 2021, 7:32pm

I store the rightmost occurrences of all numbers from 1 to n and dump all of them in a set(note that all of them would be unique so we don’t have to handle duplicates) and then we iterate over all indices from 1 to m deleting the right indices of the numbers which we’ve encountered. and check what is the number of elements that I’ve to delete from the right end and it’s trivial to see that it’d just be the greatest value in the set as it hasn’t been covered by the right end and is most deeply embedded in the array, and just take the min overall indices.
Example:
A=[1,2,3,2,1,1,2]
R=[2,1,5]
S=[1,2,5] (sorted R)
Here R_i represents the minimum number of elements that we have to delete from the right end to encounter the first occurrence of i. → R_1=2 as we have to delete at least 2 elements to encounter a 1,R_3=5 as we have to delete at least 5 elements from right to encounter a 3.
Now we iterate on A and calculate the answer for each index.

i=1
Delete R_{A_1} from S as we have considered A_1 from the left so, S would look like,
S=[1,5]
so answer for this index is 1+\max(S)=1+5=6
i=2
Delete R_{A_2} from S
S=[5]
answer will be 2+5 =7
i=3
Delete R_{A_3} from S
answer will be 3+0 =3

similarly for all i \le M
and taking minimum over all indices gives 3 (min(6,7,3…)) as the answer

I think I chose a stupid example, but the idea should be clear I suppose, do let me know if it isn’t.
@cfacto

prabhu4 · May 30, 2021, 9:23pm

Great Editorial !

ariselpy · May 30, 2021, 9:54pm

Mine is similar but with O(m + nlogn).

Considering for each unique number, use (leftmost occurrence, -rightmost occurrence) as a 2-D point to present the number.

Then for a (i, j) (pop i from left and j from right), the number of points that are not occur are in the area where x > i && y > j.

So sliding the points from the bigest x, then required minimum y is the largest y in the area that has already slided…

cubefreak777 · May 30, 2021, 9:58pm

I did it here you can check it

cricket_99 · May 31, 2021, 7:23am

in last cases it fails i don’t know why ,

#include <bits/stdc++.h>

using namespace std;

#define int long long int
#define ff first
#define ss second
#define pb push_back
#define mkp make_pair
#define pii pair<int , int>
#define nl printf("\n") ;
#define pn printf(“NO\n”) ;
#define py printf(“YES\n”) ;
#define fill(a , x) memset(a , x , sizeof(a)) ;
#define vvi vector<vector>
#define vi vector

const int mod = 1e9 + 7 , N = 4e6 + 2 ;

bool cmp(pii& a , pii& b){
if(a.ss != b.ss) return a.ss < b.ss ;
else return a.ff < b.ff ;
}

int modval(int n){ return n % mod ; }

int modadd(int a , int b){ return modval(modval(a) + modval(b)) ; }

int modsub(int a , int b){ return modval(modval(a) + modval(modadd(mod , -b) + mod)) ; }

int modmul(int a , int b){ return modval(modval(a) * modval(b)) ; }

void chef_subarrays(){
int n , m ;
cin >> n >> m ;
int a[n + 1] , b[n + 1] , arr[m + 1] ;
for(int i = 1 ; i <= n ; i++) a[i] = -1 , b[i] = -1 ;
stack st ;
st.push(0) ;
for(int i = 1 , x ; i <= m ; i++){
cin >> arr[i] ;
if(a[arr[i]]==-1) a[arr[i]] = i , st.push(i) ;
b[arr[i]] = i ;
}
int x , y = m , ans = m ;
while(not st.empty()){
x = st.top() , st.pop() ;
if(x!=0){
y = min(b[arr[x]] , y) ;
x = st.top() ;
ans = min(x + m - y + 1 , ans) ;
}
}
printf("%lld\n",ans) ;
}

int32_t main() {
// your code goes here
int t = 1 ;
scanf("%lld",&t) ;
while(t–) chef_subarrays() ;
return 0;
}

but in the below i’ve just added reverse traversal of previous , then it goes right
can someone tell me why it’s happening

#include <bits/stdc++.h>

using namespace std;

#define int long long int
#define ff first
#define ss second
#define pb push_back
#define mkp make_pair
#define pii pair<int , int>
#define nl printf("\n") ;
#define pn printf(“NO\n”) ;
#define py printf(“YES\n”) ;
#define fill(a , x) memset(a , x , sizeof(a)) ;
#define vvi vector<vector>
#define vi vector

const int mod = 1e9 + 7 , N = 4e6 + 2 ;

bool cmp(pii& a , pii& b){
if(a.ss != b.ss) return a.ss < b.ss ;
else return a.ff < b.ff ;
}

int modval(int n){ return n % mod ; }

int modadd(int a , int b){ return modval(modval(a) + modval(b)) ; }

int modsub(int a , int b){ return modval(modval(a) + modval(modadd(mod , -b) + mod)) ; }

int modmul(int a , int b){ return modval(modval(a) * modval(b)) ; }

void chef_subarrays(){
int n , m ;
cin >> n >> m ;
int a[n + 1] , b[n + 1] , arr[m + 1] ;
for(int i = 1 ; i <= n ; i++) a[i] = -1 , b[i] = -1 ;
stack st ;
st.push(0LL) ;
for(int i = 1 , x ; i <= m ; i++){
cin >> arr[i] ;
if(a[arr[i]]==-1) a[arr[i]] = i , st.push(i) ;
b[arr[i]] = i ;
}
int x , y = m , ans = m ;
while(not st.empty()){
x = st.top() ;
st.pop() ;
if(x!=0){
y = min(b[arr[x]] , y) ;
x = st.top() ;
ans = min(x + m - y + 1 , ans) ;
}
}
for(int i = 1 ; i <= n ; i++) a[i] = -1 , b[i] = -1 ;
st.push(m+1) ;
for(int i = m ; i >= 1 ; i–){
if(a[arr[i]]==-1) a[arr[i]] = i , st.push(i) ;
b[arr[i]] = i ;
}
y = 0 ;
while(not st.empty()){
x = st.top() ;
st.pop() ;
if(x!=m+1){
y = max(y , b[arr[x]]) ;
x = st.top() ;
ans = min(y + m - x + 1 , ans) ;
}
}
printf("%lld\n",ans) ;
}

int32_t main() {
// your code goes here
int t = 1 ;
scanf("%lld",&t) ;
while(t–) chef_subarrays() ;
return 0;
}

parth_2_8 · May 31, 2021, 12:25pm

Can some one please explain me how to write the code in python.
I have understood the logic but unable to write the code.

karnivas007 · May 31, 2021, 12:58pm

man your code is super complicated. please explain it …looks way more compact tho

karnivas007 · May 31, 2021, 1:06pm

awesome solution